2010 год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Сравнение площадей (4 класс).
Содержание
- 1. Презентация по математике Сравнение площадей (4 класс).
- 2. Цели и задачи:Цель: 1.Сравнить площади четырёхугольников равного
- 3. Прогнозируемый результат В результате выполнения проекта
- 4. Гипотеза В древних египетских и
- 5. Найти информацию о нахождении площадей древними учёными.Глава
- 6. В Киевской Руси мер площади, как квадратных
- 7. Легенда царицы Дидоны Дидона выторговала у вождей
- 8. Карфаген
- 9. Сравнить площади четырёхугольников одинакового периметра.Глава «Практическая» S=9*9=81
- 10. Слайд 10
- 11. Глава «Практическая» 14 см 4 смSпрямоугольника
- 12. Глава «Практическая»
Цели и задачи:Цель: 1.Сравнить площади четырёхугольников равного периметра.2.Расширить знания о площадях четырёхугольников как с математической точки зрения, так и с других точек зрения ( исторической, географической, в повседневной жизни)Задачи:1.Через конкретно-практические задачи сравнивать по площади
Слайд 1
Работу выполнила:
Голомидова Катя.
Руководитель:СтепановаТ.Ю.
Сравнение площадей
МОУ «Приволжская ООШ»
Слайд 2Цели и задачи:
Цель: 1.Сравнить площади четырёхугольников равного периметра.
2.Расширить знания о площадях
четырёхугольников как с математической точки зрения, так и с других точек зрения
( исторической, географической, в повседневной жизни)
Задачи:1.Через конкретно-практические задачи сравнивать по площади разные четырёхугольники данного периметра..
2. Найти сведения вычисления площадей в древности.
3.Через конкретно-практические задачи применять вычисление площади в быту.
( исторической, географической, в повседневной жизни)
Задачи:1.Через конкретно-практические задачи сравнивать по площади разные четырёхугольники данного периметра..
2. Найти сведения вычисления площадей в древности.
3.Через конкретно-практические задачи применять вычисление площади в быту.
Слайд 3Прогнозируемый результат
В результате выполнения проекта «Сравнение площадей четырёхугольников» я
должна узнать:
если периметры разных четырёхугольников одинаковые, то одинаковые ли их площади;
знать сведения вычисления площадей в древности;
самостоятельно работать с дополнительной литературой.
если периметры разных четырёхугольников одинаковые, то одинаковые ли их площади;
знать сведения вычисления площадей в древности;
самостоятельно работать с дополнительной литературой.
Слайд 4Гипотеза
В древних египетских и вавилонских математических документах встречаются материалы, которые
дают нам информацию о потребности измерения расстояний и площадей. Она привела к появлению зачатков геометрических знаний в глубине тысячелетий. Площадь интересно изучать, как с математической точки зрения, так и с других точек зрения
( исторической, географической, в повседневной жизни)
( исторической, географической, в повседневной жизни)
Слайд 5Найти информацию о нахождении площадей древними учёными.
Глава «История»
Вычисление площадей уже в
древности было одной из важнейших задач практической геометрии (разбивка земельных участков). Древнегреческие учёные располагали точными правилами вычисления площадей.
Эвклид – древнегреческий математик.
В книгу I включена теория вычисления площадей геометрических фигур.
Эвклид – древнегреческий математик.
В книгу I включена теория вычисления площадей геометрических фигур.
Слайд 6
В Киевской Руси мер площади, как квадратных мер, судя по сохранившимся
источникам, не было. Хотя, древнерусские зодчие и землемеры имели о них представление.
Меры площади нужны были для определения размеров земельных участков.
В 1916 году были узаконены квадратный километр, квадратный метр, квадратный дециметр, квадратный сантиметр, квадратный миллиметр, а для земельных площадей — ар и гектар.
В 1916 году были узаконены квадратный километр, квадратный метр, квадратный дециметр, квадратный сантиметр, квадратный миллиметр, а для земельных площадей — ар и гектар.
Измерение площадей на Руси.
Слайд 7
Легенда царицы Дидоны
Дидона выторговала у вождей племен, населявших север Африки,
право владеть «клочком земли, который покроет воловья шкура». Коварная финикийская царица и не думала класть шкуру на землю — нет, она разрезала ее на тонкие ремни, связала их вместе и этой длинной веревкой вознамерилась огородить свое будущее владение. И тут перед ней — впервые за всю человеческую историю — встала задача, которую много веков спустя назовут изопериметрической: какую форму должна иметь замкнутая линия, чтобы площадь, заключенная внутри нее, получилась наибольшей?
Догадалась ли Дидона, что искомая фигура — круг? Кто знает...
Мы говорим о периметре фигур.
Догадалась ли Дидона, что искомая фигура — круг? Кто знает...
Мы говорим о периметре фигур.
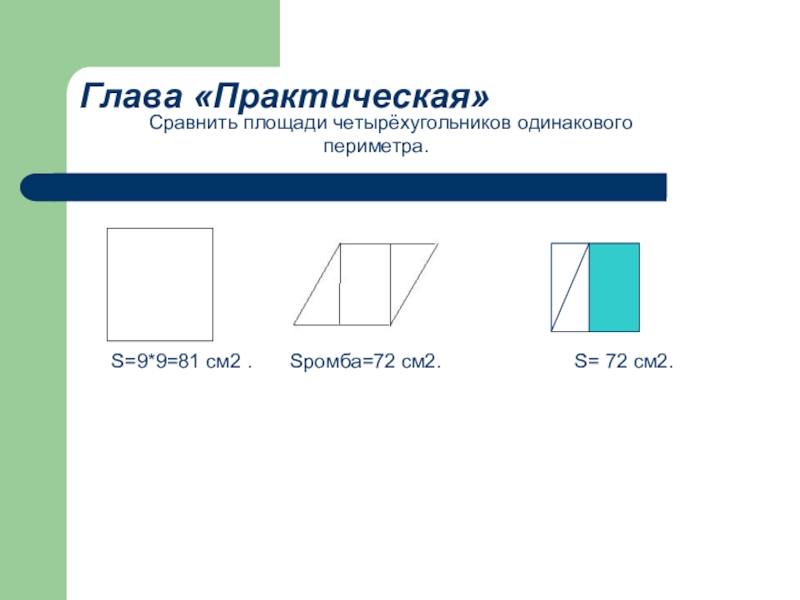
Слайд 9Сравнить площади четырёхугольников одинакового периметра.
Глава «Практическая»
S=9*9=81 см2 .
Sромба=72 см2. S= 72 см2.
Слайд 10
10 см
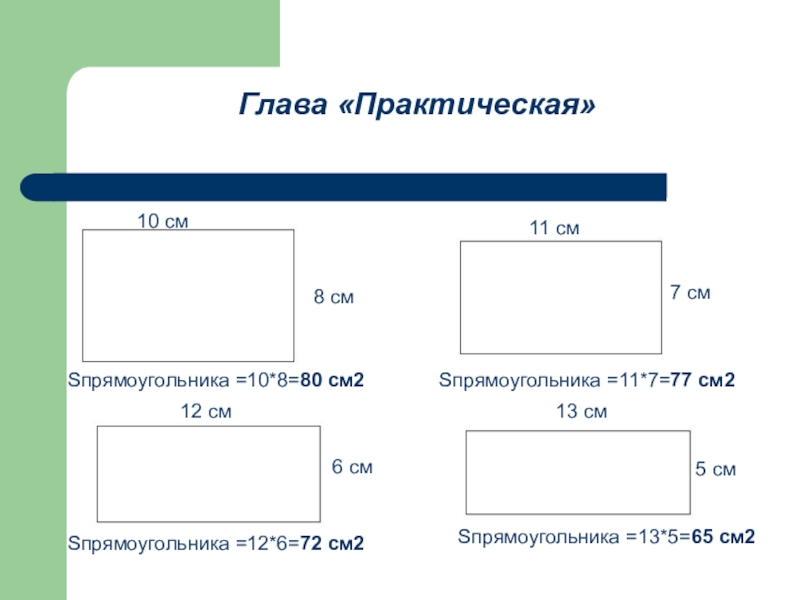
Sпрямоугольника =10*8=80 см2
8 см
11 см
7 см
Sпрямоугольника =11*7=77 см2
Глава «Практическая»
12 см
6 см
Sпрямоугольника =12*6=72 см2
13 см
5 см
Sпрямоугольника =13*5=65 см2
Слайд 11Глава «Практическая»
14 см
4 см
Sпрямоугольника =14*4=56 см2
15 см
3 см
Sпрямоугольника =15*3=45 см2
16 см
2 см
Sпрямоугольника =16*2=32 см2
17 см
Sпрямоугольника =17*1=17 см2
1 см
Слайд 12
Глава «Практическая»
Вывод
Итак, площадь квадрата больше площадей четырёхугольников
равного с ним периметра.
Из двух правильных многоугольников с равным периметром большую площадь имеет тот, у которого число углов больше;
из всех плоских фигур с равным периметром наибольшую площадь имеет круг.
