Презентация, доклад по математике Решение задач по теории вероятностей. Подготовка к ОГЭ и ЕГЭ

Содержание

Теория вероятностей – раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Слайд 1Решение задач по теории вероятностей.
Подготовка к ОГЭ и ЕГЭ

Решение задач по теории вероятностей.Подготовка к ОГЭ и ЕГЭ

Слайд 2Теория вероятностей – раздел математики, изучающий закономерности случайных явлений: случайные события,

случайные величины, их свойства и операции над ними.
Теория вероятностей – раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции

Слайд 3Случай, случайность — с ними мы встречаемся повседневно: случайная встреча, случайная

поломка, случайная находка, случайная ошибка. Этот ряд можно продолжать бесконечно. Казалось бы, тут нет места для математики, но и здесь наука обнаружила

интересные закономерности - они позволяют человеку уверенно чувствовать себя при встрече со
случайными
событиями.

Случай, случайность — с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная находка, случайная ошибка. Этот

Слайд 4Развитие теории вероятностей с момента зарождения этой науки и до настоящего

времени было несколько своеобразным. На первом этапе истории этой науки она рассматривалась как занимательный “пустячок”, как собрание курьезных задач, связанных в первую очередь с азартными играми в кости и карты.
Развитие теории вероятностей с момента зарождения этой науки и до настоящего времени было несколько своеобразным. На первом

Слайд 5Никаких специальных методов решения задач нет. Этот период кончается работами

Дж. Кардано, 
Л. Пачоли, Н. Тарталья.

Д. Кардано

Н. Тарталья

Л. Пачоли

Никаких специальных методов решения задач нет. Этот период кончается работами Дж. Кардано,  Л. Пачоли, Н. Тарталья.

Слайд 6К середине XVII в. вероятностные вопросы и проблемы, возникающие в статистике,

в практике страховых обществ, при обработке результатов наблюдений и в других областях, привлекли  внимание ученых.

Б. Паскаль

П. Ферма

X. Гюйгенс

К середине XVII в. вероятностные вопросы и проблемы, возникающие в статистике, в практике страховых обществ, при обработке

Слайд 7Следующий период развития теории вероятностей начинается с работы Якоба Бернулли «Искусство

предположений». В  ней впервые была доказана первая предельная теорема – простейший случай закона больших чисел.


Теорема Бернулли: Вероятность Рn(k) наступления ровно k «успехов» в n независимых повторениях одного и того же испытания вычисляется по формуле


q – вероятность «успеха»
r = 1 – q – вероятность «неудачи» в
отдельном испытании.

Следующий период развития теории вероятностей начинается с работы Якоба Бернулли «Искусство предположений». В  ней впервые была доказана первая предельная

Слайд 8Современный период развития теории вероятностей начался с установления аксиоматики. Этого прежде

всего требовала практика, так как для успешного применения теории вероятностей в физике, биологии и других областях науки, а также в технике и военном деле необходимо было уточнить и привести в стройную систему ее основные понятия.
Современный период развития теории вероятностей начался с установления аксиоматики. Этого прежде всего требовала практика, так как для

Слайд 9
Первые работы этого периода связаны с именами С.Бернштейна, Р.Мизеса, Э.Бореля.

Первые работы этого периода связаны с именами С.Бернштейна, Р.Мизеса, Э.Бореля.

Слайд 10ПОНЯТИЕ ВЕРОЯТНОСТИ
В толковом словаре С.И. Ожегова и Н.Ю. Шведовой:
«Вероятность – возможность

исполнения, осуществимости чего-нибудь».


Основатель современной теории вероятностей А.Н.Колмогоров:
«Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях».
ПОНЯТИЕ ВЕРОЯТНОСТИВ толковом словаре С.И. Ожегова и Н.Ю. Шведовой:«Вероятность – возможность исполнения, осуществимости чего-нибудь».Основатель современной теории вероятностей

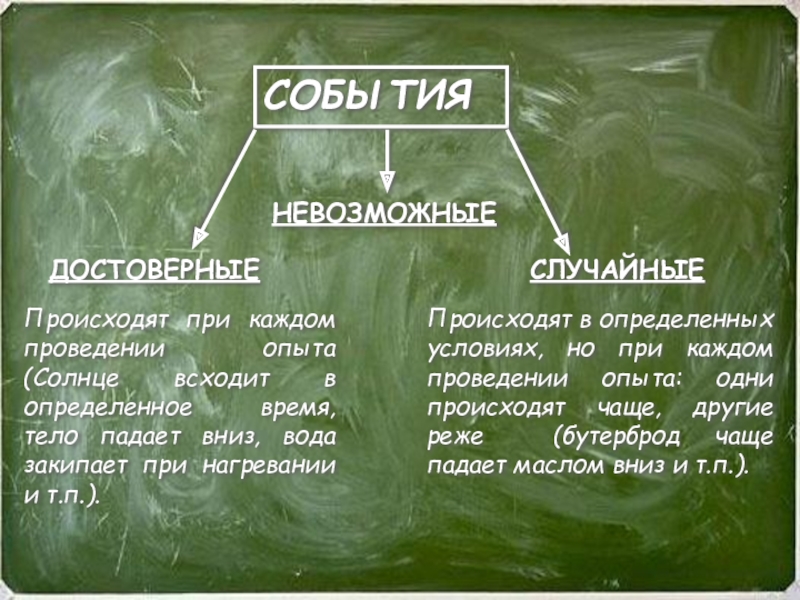
Слайд 11СОБЫТИЯ
Происходят при каждом проведении опыта (Солнце всходит в определенное время, тело

падает вниз, вода закипает при нагревании и т.п.).

ДОСТОВЕРНЫЕ

НЕВОЗМОЖНЫЕ

СЛУЧАЙНЫЕ

Происходят в определенных условиях, но при каждом проведении опыта: одни происходят чаще, другие реже (бутерброд чаще падает маслом вниз и т.п.).

СОБЫТИЯПроисходят при каждом проведении опыта (Солнце всходит в определенное время, тело падает вниз, вода закипает при нагревании

Слайд 12 Оказывается, что достаточно большое число однородных случайных событий независимо

от их конкретной природы подчиняется определённым закономерностям, а именно, вероятностным закономерностям.

Установлением этих закономерностей и занимается теория вероятностей.

Определение вероятности

Оказывается, что достаточно большое число однородных случайных событий независимо от их конкретной природы подчиняется определённым

Слайд 13Классическое определение вероятности
Классическое определение вероятности было впервые дано в работах французского

математика П. Лапласа. В нём события определяются как множества равновероятных случаев.

Вероятностью р наступления случайного события А называется отношение ,



где n – число всех возможных исходов эксперимента,
а k – число всех благоприятных исходов:

p =

Классическое определение вероятностиКлассическое определение вероятности было впервые дано в работах французского математика П. Лапласа. В нём события

Слайд 14Для нахождения вероятности случайного события А при проведении некоторого испытания следует

найти:

1) число n всех возможных исходов данного испытания;
2) количество k тех исходов, в которых наступает событие А;

3) частное ; оно и будет равно

вероятности события А.

Алгоритм нахождения вероятности случайного события


Для нахождения вероятности случайного события А при проведении некоторого испытания следует найти:1) число n всех возможных исходов

Слайд 15Статистическое определение вероятности
Статистические закономерности были впервые обнаружены на примере азартных игр,

т.е. на примере тех испытаний, которые характеризуются равновозможностью исходов. В последовательности одинаковых испытаний можно обнаружить устойчивость некоторых средних характеристик.
Статистическое определение вероятностиСтатистические закономерности были впервые обнаружены на примере азартных игр, т.е. на примере тех испытаний, которые

Слайд 16Частостью какого-либо события в данной серии из n испытаний называется отношение

числа k тех испытаний, в которых событие А наступает, к общему числу испытаний n.

Частость испытания А обозначается

,

где k – число экспериментов , в которых появилось событие А, n – общее число экспериментов.


Частостью какого-либо события в данной серии из n испытаний называется отношение числа k тех испытаний, в которых

Слайд 17Опыт человечества
Вероятность попасть под дождь

в Лондоне гораздо выше, чем в пустыне Сахара.

Весь наш жизненный опыт подсказывает, что любое событие считается тем более вероятным, чем чаще оно происходит. Значит, вероятность должна быть каким-то образом связана с частотой.

Опыт человечестваВероятность попасть под дождь

Слайд 18Фундаментальным свойством относительных частот является тот факт, что с увеличением числа

опытов относительная частота случайного события постепенно стабилизируется и приближается к вполне определенному числу, которое и следует считать его вероятностью.
Фундаментальным свойством относительных частот является тот факт, что с увеличением числа опытов относительная частота случайного события постепенно

Слайд 19

Решение задач

Задачи по теории вероятностей в КИМах ОГЭ встречаются под №19, а в КИМах ЕГЭ под №5.

В данной презентации задачи условно разделены
по группам.



Решение задачЗадачи по теории вероятностей в

Слайд 20Задачи про жребий
Задача

Папа, мама, сын и дочка бросили жребий –

кому мыть посуду. Найдите вероятность того, что посуду будет мыть мама.

Решение:
Всего в задаче указано 4 человека, то есть n=4. При этом меня устраивает только один вариант, то есть k=1. имеем p=k/n=1/4=0,25

Ответ: 0,25

Задачи про жребийЗадача Папа, мама, сын и дочка бросили жребий – кому мыть посуду. Найдите вероятность того,

Слайд 21Задачи про выступления на конкурсе
Задача

Конкурс исполнителей проводится в 5 дней.

Всего заявлено 50 выступлений – по одному от каждой страны. В первый день 26 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жребием. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
Задачи про выступления на конкурсеЗадача Конкурс исполнителей проводится в 5 дней. Всего заявлено 50 выступлений – по

Слайд 22Решение:

Поскольку всего заявлено 50 выступлений, то n=50. Теперь посмотрю, сколько выступлений

состоится в каждый из дней конкурса. По условию, на первый день запланировано 26 выступлений. Значит, на другие дни останется 50 – 26=24 выступления.

Эти выступления распределены поровну между оставшимися 4 днями, то есть на каждый день приходится по 24:4=6 выступлений. Получаю следующее распределение по дням;

Решение:Поскольку всего заявлено 50 выступлений, то n=50. Теперь посмотрю, сколько выступлений состоится в каждый из дней конкурса.

Слайд 23Число участ-ников
День
6
6
6
6
26
5
4
3
2
1
Меня интересует третий день, на который приходится 5 выступлений. Таким

образом, k=6. Находим вероятность:
P=k/n=6/50=0,12

Ответ: 0,12
Число участ-никовДень66662654321Меня интересует третий день, на который приходится 5 выступлений. Таким образом, k=6. Находим вероятность: P=k/n=6/50=0,12 Ответ:

Слайд 24Задачи про игральные кости (кубики) или монеты
Задача

Игральную кость (кубик) бросили

один раз. Какова вероятность того, что выпало менее 4 очков?

Решение:

У кубика 6 граней, поэтому всего возможно 6 вариантов: 1, 2, 3, 4, 5 и 6 очков. Получает, что n=6 – по числу граней. Меня интересуют случаи, когда выпадает менее 4 очков. Другими словами, если выпадает 1, 2 или 3 очка, меня это устраивает. Всего таких вариантов k=3. Находим вероятность: p=k/n=3/6=0,5
Ответ: 0,5

Задачи про игральные кости (кубики) или монетыЗадача Игральную кость (кубик) бросили один раз. Какова вероятность того, что

Слайд 25Задача

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того,

что оба раза выпадет орел.

Решение:

Рассмотрим все возможные варианты: орёл – решка, орёл – орёл, решка – решка, решка – орёл, то есть всего 4 варианта и n=4. Случай, когда оба раза выпадет орел – единственный, значит k=1. вероятность того, что оба раза выпадет орёл p=k/n=1/4=0,25

Ответ: 0,25
Задача В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что оба раза выпадет орел.Решение:Рассмотрим все

Слайд 26Задача

Таня и Нина играют в кости. Они бросают кость по

одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 6 очков. Найдите вероятность того, что Таня выиграла.


Задача Таня и Нина играют в кости. Они бросают кость по одному разу. Выигрывает тот, кто выбросил

Слайд 273
4
2
5
1
Нина
3
2
4
1
5
Таня
Эту задачу можно решить с помощью таблицы:
Для Тани удачных вариантов 2,

а всего игр возможно 5, получаем: p=2/5=0,4

Ответ:0,4
34251Нина32415ТаняЭту задачу можно решить с помощью таблицы:Для Тани удачных вариантов 2, а всего игр возможно 5, получаем:

Слайд 28Задачи о соревнованиях
Задача

На соревнования по метанию ядра приехали 2 спортсмена

из Великобритании, 2 из Испании и 4 из Швейцарии. Порядок выступлений определяется жребием. Найдите вероятность того, что восьмым будет выступать спортсмен из Испании.
Задачи о соревнованияхЗадача На соревнования по метанию ядра приехали 2 спортсмена из Великобритании, 2 из Испании и

Слайд 29Решение:

Для начала выясню, сколько всего спортсменов приехало на соревнования: 2 +

2 + 4 = 8 спортсменов. Значит n=8. Меня интересуют лишь спортсмены из Испании, которых было 2. Поэтому k=2. Найду вероятность: p=2/8=1/4=0,25

Ответ: 0,25

Решение:Для начала выясню, сколько всего спортсменов приехало на соревнования: 2 + 2 + 4 = 8 спортсменов.

Слайд 30Задача

Перед началом футбольного матча судья бросает монету, чтобы определить, какая

из команд будет первая владеть мячом. Команда «Меркурий» по очереди играет с

командами «Марс», «Юпитер» и «Уран». Найдите вероятность того, что во всех матчах право владеть мячом выиграет команда «Меркурий».

Задача Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом.

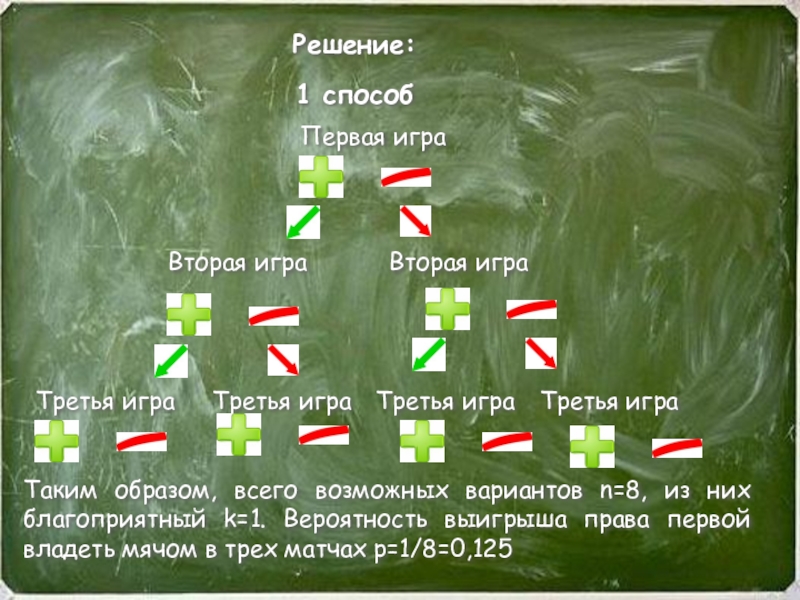
Слайд 31Решение:

1 способ
Первая игра
Вторая игра
Вторая игра
Третья игра
Третья игра
Третья игра
Третья игра
Таким образом, всего

возможных вариантов n=8, из них благоприятный k=1. Вероятность выигрыша права первой владеть мячом в трех матчах p=1/8=0,125
Решение:1 способПервая играВторая играВторая играТретья играТретья играТретья играТретья играТаким образом, всего возможных вариантов n=8, из них благоприятный

Слайд 32 Вероятность того, что команда «Меркурий» выиграет право

первой владеть мячом в игре с командой «Марс» равна 0,5. Аналогично можно рассуждать о результатах жеребьевки и в других матчах, поскольку эти события независимы друг от друга.
Воспользуемся правилом
умножения вероятностей:
0,5·0,5·0,5=0,125

Ответ: 0,125

2 способ

Вероятность того, что команда «Меркурий» выиграет право первой владеть мячом в игре с

Слайд 33Задачи об экзаменах
Задача

В сборнике билетов по физике всего 20

билетов, в 6 из них встречается вопрос по электростатике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику встретится вопрос по электростатике.

Решение:

Из условия следует, что n=20, а k=6. Значит, вероятность того, что в случайно выбранном на экзамене билете школьнику встретится вопрос по электростатике P=6/20=0,3

Ответ: 0,3

Задачи об экзаменах Задача В сборнике билетов по физике всего 20 билетов, в 6 из них встречается

Слайд 34Также вы можете решать тестовые задания на сайте www.fipi.ru

Также вы можете решать тестовые задания на сайте www.fipi.ru

Слайд 35В презентации использованы материалы учебного проекта обучающейся 11б класса Зайцевой Ольги



В презентации использованы материалы учебного проекта обучающейся 11б класса Зайцевой Ольги
Скачать презентацию

Похожие презентации

Презентация: Графическое решение квадратных уравнений Презентация: Графическое решение квадратных уравнений 207
Учить - значит удивлять. Учить - значит удивлять. 222
Животные в космосе. Животные в космосе. 251
Презентация по математике на тему Подобные слагаемые (6 класс) Презентация по математике на тему Подобные слагаемые (6 класс) 178
Презентация по математике на тему Проценты Презентация по математике на тему Проценты 248
Презентация к уроку математики по теме Задачи на увеличение и уменьшение числа на несколько единиц Презентация к уроку математики по теме Задачи на увеличение и уменьшение числа на несколько единиц 183

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Яндекс.Метрика

Обратная связь

Email: Нажмите что бы посмотреть