Выполнил:
ученик 9 класса
Кравченко Виталий
Руководитель:
учитель математики
Нечаева
Елена Николаевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Решение уравнений высших порядков ( 3-й и 4-ой степени)
Содержание
- 1. Презентация по математике Решение уравнений высших порядков ( 3-й и 4-ой степени)
- 2. Основные методы решения уравнений высших порядков
- 3. Уравнения вида ax3 + bx2 +
- 4. Решу уравнение х3 -7х+6=0
- 5. 2.Метод деления на многочлен
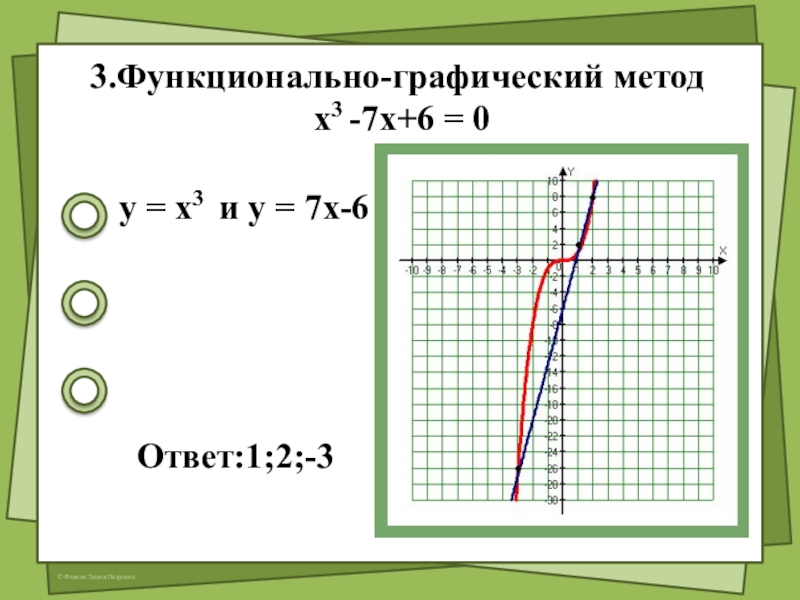
- 6. 3.Функционально-графический метод х3 -7х+6 = 0
- 7. Уравнение четвертой степени общего вида ax4 +
- 8. 2.Деление на многочлен Х4 - Х3-13 Х
- 9. Биквадратное уравнение вида ax4 + bx2 + с = 0. 3.Метод: введение новой
- 10. Задание:Решите уравнение Х3+2Х2- 5Х - 6 =
Основные методы решения уравнений высших порядков 1. Метод разложения на множители левой части уравнения. 2.Метод введения новой переменной.
Слайд 2Основные методы решения уравнений высших порядков
1. Метод разложения на множители
левой части уравнения.
2.Метод введения новой переменной.
3.Функционально-графический метод
левой части уравнения.
2.Метод введения новой переменной.
3.Функционально-графический метод
Слайд 3Уравнения вида ax3 + bx2 + cx + d = 0,
где a ≠ 0,
называются уравнениями 3-ей степени
Уравнение вида
x 3 + px + q = 0
называется приведённым
кубическим уравнением
Известные формулы Кардано для решения уравнений этого типа очень сложны и почти не применяются на практике.
Слайд 4Решу уравнение
х3 -7х+6=0 разными способами
1. Разложение на множители
х3 -7х + 6 =0
х3 - х2 + х2 – х - 6х + 6=0
х2 (х-1)+ х(х-1)-6(х-1)=0
(х-1)(х2 + х - 6) = 0
х-1=0 или х2 + х – 6 = 0
х1 =1 х2 =-3 х3 = 2
Ответ: 1; 2; -3
х3 -7х + 6 =0
х3 - х2 + х2 – х - 6х + 6=0
х2 (х-1)+ х(х-1)-6(х-1)=0
(х-1)(х2 + х - 6) = 0
х-1=0 или х2 + х – 6 = 0
х1 =1 х2 =-3 х3 = 2
Ответ: 1; 2; -3
Слайд 52.Метод деления на многочлен
х3 -7х+6 =
0 делители 6: ±1; ±2; ±3; ±6
х3-7х+6 =(х-1)(х2 +х-6)=0
х-1=0 или х2 +х-6=0
х1 =1 х2 =-3 х3 = 2
Ответ: 1; 2; -3
х3-7х+6 =(х-1)(х2 +х-6)=0
х-1=0 или х2 +х-6=0
х1 =1 х2 =-3 х3 = 2
Ответ: 1; 2; -3
1³-7+6=0
x³-0х2-7x+6 x-1
x³-x² x²+x-6
x²-7x
x²-x
-6x+6
-6x+6
0
Слайд 7Уравнение четвертой степени общего вида ax4 + bx3 + cx2 + dx + e
= 0 где а ≠ 0
1.Разложение на множители
x4 + 2x3 + 5x2 + 4x – 12 = 0
x4 + 2x3 + 5x2 + 10x – 6x – 12 = 0
(x4 + 2x3) + (5x2 + 10x) – (6x + 12 ) = 0
x3 (x+2) +5х (х+2) – 6 (х+2) =0
(x + 2) (x3 + 5x – 6) = 0
(x + 2)(x – 1)(x2 + x + 6) = 0
x1 = -2, x2 = 1.
Ответ: -2 ; 1
Слайд 82.Деление на многочлен Х4 - Х3-13 Х -15=0 -1 делитель числа -15
(1+1+13-15=0)
Х4 - Х3-13 Х -15 = (Х+1)(Х-3)(Х2 +Х +5) = 0
Х+1 =0 или Х-3=0 или Х2 +Х +5 =0 (Д<0)
Х1=-1 Х 2=3
Ответ: -1; 3
Слайд 9Биквадратное уравнение вида ax4 + bx2 + с = 0.
3.Метод: введение новой переменной
x4 + 5x2 – 36 = 0.
Замена y = x2.
У2+ 5У-36=0
У1*У2 =-36= -9*4 У1=-9
У1 + У1 =-5= -9+4 У2 =4
X2 =-9 x2 =4
Корней нет х1 =2 х2 =-2
Ответ: 2; -2
Замена y = x2.
У2+ 5У-36=0
У1*У2 =-36= -9*4 У1=-9
У1 + У1 =-5= -9+4 У2 =4
X2 =-9 x2 =4
Корней нет х1 =2 х2 =-2
Ответ: 2; -2
Слайд 10Задание:Решите уравнение
Х3+2Х2- 5Х - 6 = 0
Делители -6: ±1; ±2; ±3; ±6
-1 корень уравнения (-1+2+5-6=0)
Х3+2Х2- 5Х - 6 = (Х+1)(Х2+Х -6) = 0
Х+1= 0 или Х2+Х -6=0
Х1 =-1 Х2 =-3 Х3 = 2
Ответ: -1; -3; 2
-1 корень уравнения (-1+2+5-6=0)
Х3+2Х2- 5Х - 6 = (Х+1)(Х2+Х -6) = 0
Х+1= 0 или Х2+Х -6=0
Х1 =-1 Х2 =-3 Х3 = 2
Ответ: -1; -3; 2
