- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Реальные задачи Я.И. Перельмана
Содержание
- 1. Презентация по математике Реальные задачи Я.И. Перельмана
- 2. В подборке представлены задачи с реальным содержанием:
- 3. 1 Задачи из обиходной жизни
- 4. Задача 1В каком месте незастроенного треугольного двора
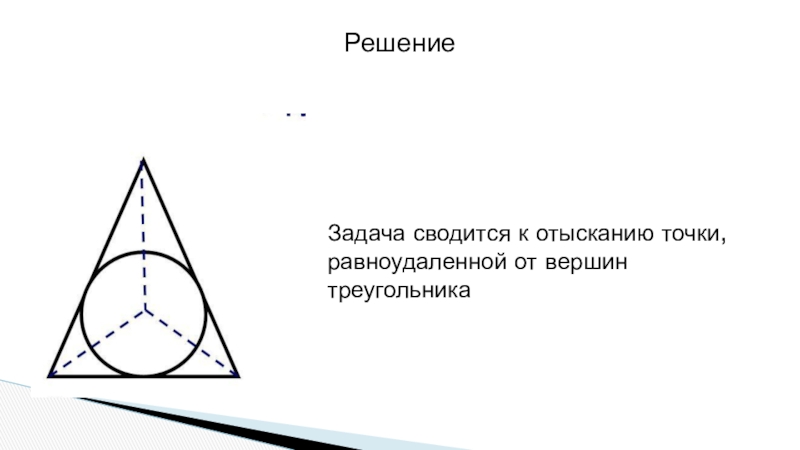
- 5. РешениеЗадача сводится к отысканию точки, равноудаленной от вершин треугольника
- 6. Задача 2Желая проверить, имеет ли отрезанный кусок
- 7. РешениеНет, недостаточна. Указанный прием убеждает лишь в
- 8. Задача 3Стакан вплотную обставлен соприкасающимися с ним и между собой стаканами такой же величины. Сколько их?
- 9. РешениеИз рисунка видно, что прямые, соединяющие центры
- 10. Задача 4Во сколько раз объем мясистой части
- 11. РешениеТак как диаметр вишни втрое больше диаметра
- 12. Задача 5Какие яйца выгоднее покупать: 60-миллиметровые(по длине) по 1 руб., или 55-миллиметровые по 75 коп.?
- 13. РешениеОбъем меньшего яйца (то есть колличество питательных
- 14. 2. Задачи из техники и сельского хозяйства
- 15. Задача 1Жестяники и столяры нередко пользуются следующим
- 16. Длина окружности получается при этом равной6r+(r-r √¯2/2)=
- 17. Задача 2Из цилиндрического бревна нужно выпилить брус наибольшего веса. Как это сделать?
- 18. Решение
- 19. Задача 3Жестянщикуизготовить из квадратного куска жести в
- 20. Слайд 20
- 21. 3. Задачи из мироведения
- 22. Задача 1Вообразим, что земной шар вытянут в
- 23. Ответ- для большинства неожиданный- получается из уравнения1/4πx²
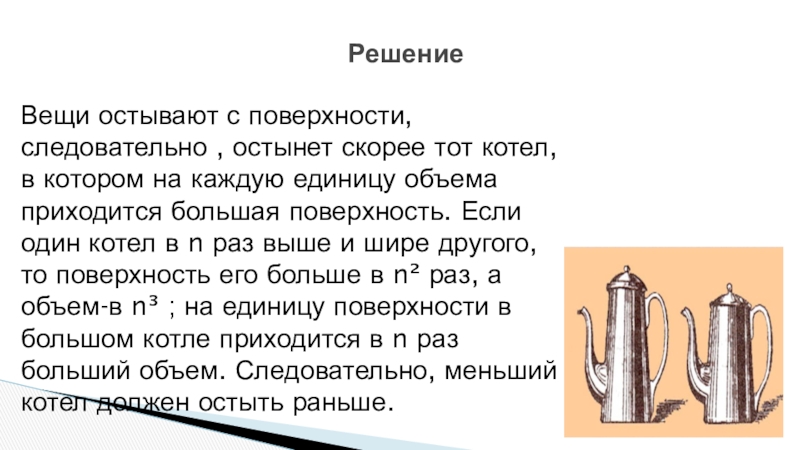
- 24. Задача 2Два котла, большой и малый, одинакового
- 25. РешениеВещи остывают с поверхности, следовательно , остынет
- 26. Задач 3 У древних индусов был обычай
- 27. Решение:
- 28. 4 Задачи из живой природы
- 29. Задача 1При каждом ударе сердце человека выталкивает
- 30. РешениеИскомое ребро куба обозначим через х. Тогдах³ = 75 · 60 · 24 · 175х=260 см
- 31. Задача 2Зрачок человеческого глаза может изменять свой
- 32. РешениеКоличество пропускаемого света пропорционально площади отверстия. Следовательно,
- 33. 5. Историческая задача
- 34. Задача 1Чтобы построить прямой угол на местности,
- 35. РешениеПолучался, так как выполняются равенства5²+12²=13² и 8²+15²=17²Прямой
- 36. Задача 2Поставим себе задачу: как следовало поступить,
- 37. Задача 7 Надо воспользоваться теоремой Пифагора
Слайд 2В подборке представлены задачи с реальным содержанием: из обиходной жизни, из
Слайд 4Задача 1
В каком месте незастроенного треугольного двора нужно поместить фонарь, чтобы
Слайд 6Задача 2
Желая проверить, имеет ли отрезанный кусок материи форму квадрата, швея
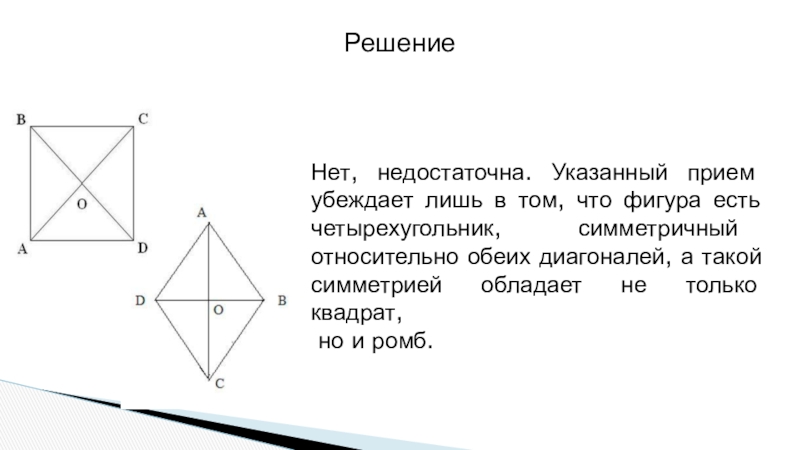
Слайд 7Решение
Нет, недостаточна. Указанный прием убеждает лишь в том, что фигура есть
но и ромб.
Слайд 8Задача 3
Стакан вплотную обставлен соприкасающимися с ним и между собой стаканами
Слайд 9Решение
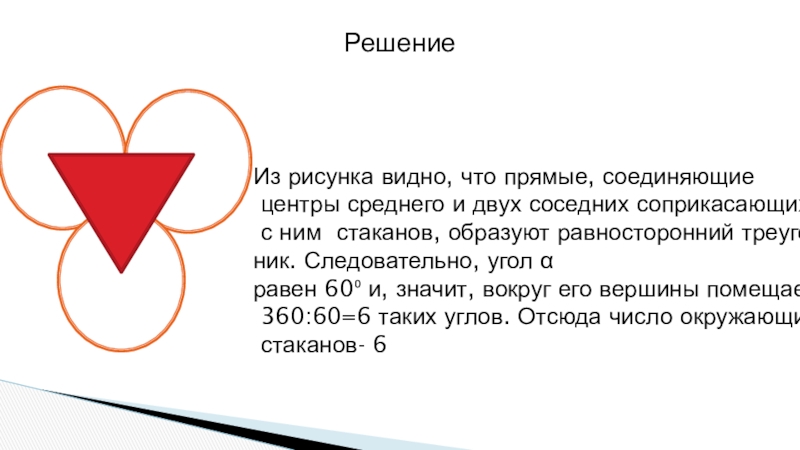
Из рисунка видно, что прямые, соединяющие
центры среднего и двух соседних
с ним стаканов, образуют равносторонний треуголь-
ник. Следовательно, угол α
равен 60⁰ и, значит, вокруг его вершины помещается
360:60=6 таких углов. Отсюда число окружающих
стаканов- 6
Слайд 10Задача 4
Во сколько раз объем мясистой части вишни больше объема косточки?
Слайд 11Решение
Так как диаметр вишни втрое больше диаметра косточки (то и другое
Слайд 12Задача 5
Какие яйца выгоднее покупать: 60-миллиметровые(по длине) по 1 руб., или
Слайд 13Решение
Объем меньшего яйца (то есть колличество питательных веществ в нем), считая
Слайд 15Задача 1
Жестяники и столяры нередко пользуются следующим приемом для определения длины
Слайд 16Длина окружности получается при этом равной
6r+(r-r √¯2/2)= 7r-0,707r=6,293r вместо 6б284r. Относительная
Решение
Слайд 18Решение
через х; тогда другая выразится через , где R – радиус кругового сечения
бревна. Площадь прямоугольника ,откуда
Так как сумма множителей и есть величина постоянная
,то произведение их будет наибольшим при
,т.е. при .Тогда же достигнет наибольшей величины и S,
т.е. площадь искомого прямоугольника.
Итак, одна сторона прямоугольника с наибольшей площадью равна , т.е.
стороне вписанного квадрата. Брус имеет больший объем, если сечение его есть квадрат, вписанный в сечение цилиндрического бревна.
Слайд 19Задача 3
Жестянщикуизготовить из квадратного куска жести в 60 см ширины коробку
Слайд 20
Пусть ширина отгибаемых полос х. Тогда ширина квадратного дна
коробки будет равна 60-2х; объем же коробки выразится
произведением
При каких х это произведение имеет наибольшее значение?
Если бы сумма трех множителей была постоянна, произведение было бы наибольшим в случае их равенства. Но здесь сумма множителей
60-2х+60-2х+120=120-3х
Не есть постоянная величина, так как изменяется с изменением х. Однако нетрудно добиться того, чтобы сумма трех множителей была постоянной: для этого достаточно лишь умножить обе части равенства на 4. Получим:
=(60-2х)(60-2х)4х
Сумма этих множителей равна 60-2х+60-2х+4х=120
величине постоянной. Значит, произведение этих множителей достигает наибольшей величины при их равенстве, т. е. когда
60-2х=4х откуда х=10
Тогда же 4 ,а с ними и достигнут своего максимума.
Итак, коробка получится наибольшего объема, если у жесткого листа отогнуть 10 см. Этот наибольший объем равен 40* 40*10=16000 куб.см. Отогнув на сантиметр меньше или больше, мы в обоих случаях уменьшим объем коробки. Действительно, 9 х 42 х 42 = 15900 куб.см.
11 х 38 х 38 = 15900 куб. см.
В том и другом случаях меньше 16000 куб.см.
Слайд 22Задача 1
Вообразим, что земной шар вытянут в цилиндрическую нить длиной от
Слайд 23Ответ- для большинства неожиданный- получается из уравнения
1/4πx² · 150 000 000=
Решение
Слайд 24
Задача 2
Два котла, большой и малый, одинакового материала и формы (или
Слайд 25Решение
Вещи остывают с поверхности, следовательно , остынет скорее тот котел, в
Слайд 26Задач 3
У древних индусов был обычай предлагать задачи в стихах:
Над озером тихим,
С полфута размером, высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Боле цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода глубока.?
Слайд 27Решение:
BC=2 фута.
Найти:CD
CD- глубина озера. Обозначим ее х. Тогда по теореме Пифагора имеем:
BD2- x2= BC2, то есть
(x+0,5)2- x2= 22,
x2+ x+ 0,25- x2= 4,
x= 3,75.
Ответ: 3,75.
Слайд 29Задача 1
При каждом ударе сердце человека выталкивает 175 см³ крови. Сердце
Слайд 31Задача 2
Зрачок человеческого глаза может изменять свой диаметр ( в зависимости
Слайд 32Решение
Количество пропускаемого света пропорционально площади отверстия. Следовательно, расширенный зрачок пропускает больше
9² / 2² = 81/4 ,то есть в 20,25 раз.
Слайд 34Задача 1
Чтобы построить прямой угол на местности, древние индусы строили на
Слайд 35Решение
Получался, так как выполняются равенства
5²+12²=13² и 8²+15²=17²
Прямой угол лежит против сторон
Слайд 36Задача 2
Поставим себе задачу: как следовало поступить, чтобы надежным образом получить
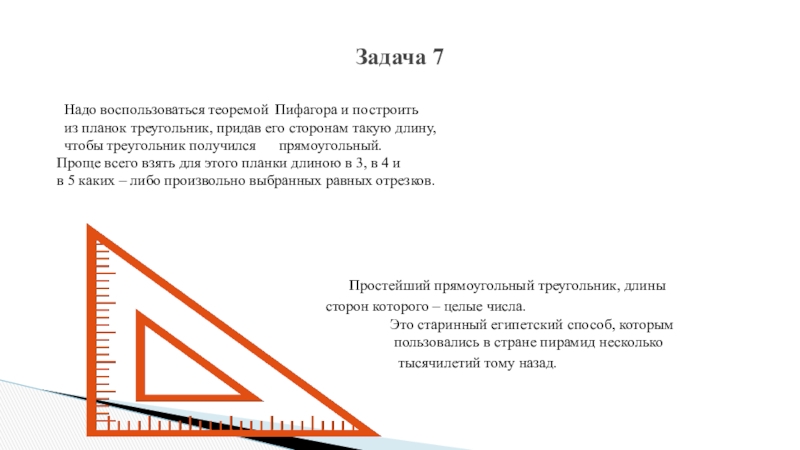
Слайд 37Задача 7
Надо воспользоваться теоремой Пифагора и построить
из планок треугольник, придав его сторонам такую длину,
чтобы треугольник получился прямоугольный.
Проще всего взять для этого планки длиною в 3, в 4 и
в 5 каких – либо произвольно выбранных равных отрезков.
Простейший прямоугольный треугольник, длины
сторон которого – целые числа.
Это старинный египетский способ, которым
пользовались в стране пирамид несколько
тысячилетий тому назад.