Г.Ф.
преподаватель КАТТ
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Развитие критического мышления через систему вопросов Блума при решении математических задач
Содержание
- 1. Презентация по математике Развитие критического мышления через систему вопросов Блума при решении математических задач
- 2. Б. Блум установил, что между
- 3. 1. Вопросы на знания: Кто, что, назови,
- 4. 3. Вопросы на применение: Примени, используй, продемонстрируй,
- 5. 5.Вопросы на синтез: Составьте, постройте, придумайте, пересмотрите,
- 6. Пример: Ученик будет учиться решать
- 7. Уравнение касательной
- 8. Задание: Написать уравнение касательной к графику функции
- 9. Уравнение касательной: y = f (x0) +
- 10. Синтез.Проверим правильность выполненной задачи: постройте данную прямую.Сколько точек потребуется для построения прямой ? (аксиома планиметрии).
- 11. Слайд 11
- 12. Спасибо за внимание
Б. Блум установил, что между уровнями мышления и ответами на вопросы, которые мы задаем, существует прямая связь. Более того, сами вопросы образуют иерархию вполне соответствующую таксономии мышления:Знание - Понимание - Применение- Анализ - Синтез
Слайд 1Развитие критического мышления через систему вопросов Блума при решении математических задач Грибанова
Слайд 2
Б. Блум установил, что между уровнями мышления и ответами
на вопросы, которые мы задаем, существует прямая связь. Более того, сами вопросы образуют иерархию вполне соответствующую таксономии мышления:
Знание - Понимание - Применение-
Анализ - Синтез - Оценка
Знание - Понимание - Применение-
Анализ - Синтез - Оценка
Слайд 3
1. Вопросы на знания: Кто, что, назови, где, когда, перечисли
– это
самый низкий уровень вопросов, требующий механического вспоминания информации.
Используются для проверки знаний.
2. Вопросы на понимание: Опиши, расскажи своими словами, подчеркни, объясни, обсуди, сравни.
задаются для раскрытия связей между идеями, фактами, определениями или ценностями.
Эти вопросы являются ключевыми, поскольку стимулируют мыслительную деятельность.
Используются для проверки знаний.
2. Вопросы на понимание: Опиши, расскажи своими словами, подчеркни, объясни, обсуди, сравни.
задаются для раскрытия связей между идеями, фактами, определениями или ценностями.
Эти вопросы являются ключевыми, поскольку стимулируют мыслительную деятельность.
Слайд 43. Вопросы на применение: Примени, используй, продемонстрируй, объясни, выбери, интерпретируй.
требуют использования
уже известной ученикам информации в новых условиях или ситуациях.
Эти вопросы достаточно сложны, так как подразумевают нестандартные ответы и поиск решений.
4. Вопросы на анализ: Почему? Проанализируйте. Разложите.
Сделайте диаграмму. Упростите. Проведите опрос. Сравните.
предусматривают разложение информации на составляющие.
Анализ требует от ученика уметь определить причины, последствия,
уметь обобщать и приходить к умозаключениям.
Эти вопросы достаточно сложны, так как подразумевают нестандартные ответы и поиск решений.
4. Вопросы на анализ: Почему? Проанализируйте. Разложите.
Сделайте диаграмму. Упростите. Проведите опрос. Сравните.
предусматривают разложение информации на составляющие.
Анализ требует от ученика уметь определить причины, последствия,
уметь обобщать и приходить к умозаключениям.
Слайд 5
5.Вопросы на синтез: Составьте, постройте, придумайте, пересмотрите, формулируйте, сделайте, спланируйте
связаны с
творческим решением проблем на основе оригинального мышления.
Вопросы на синтез дают возможность использовать собственные знания
и опыт для творческого решения проблемы.
6. Вопросы на оценку: Оцените, сравните, что самое хорошее, кто прав, почему это самое важное
-задаются учащимся для того, чтобы они вынесли собственное суждение .
Для принятия решений и решения проблем необходимо мышление именно этого уровня.
Вопросы на синтез дают возможность использовать собственные знания
и опыт для творческого решения проблемы.
6. Вопросы на оценку: Оцените, сравните, что самое хорошее, кто прав, почему это самое важное
-задаются учащимся для того, чтобы они вынесли собственное суждение .
Для принятия решений и решения проблем необходимо мышление именно этого уровня.
Слайд 6
Пример: Ученик будет учиться решать тригонометрические уравнения (например, усложненное простейшее)
Вопросы и
задания в связи с этой целью.
Знания
Что такое тригонометрическое уравнение?
Понимание
Какая разница между простейшим уравнение и записанным?
Сделайте одно «сложное» уравнение из двух простых.
Применение
Решите два простых уравнения
Решите записанное усложненное
Анализ
Назовите, как создаются «усложненные » уравнения
Сравните несколько таких уравнений. Назовите усложнения
Синтез
Напишите 3 уравнения, составленные по найденным схемам
Решите их
Оценка
Поменяйтесь тетрадями с соседом по парте и определите,
правильно ли ваш сосед понимает решение уравнений, и приготовьтесь ответить на вопросы.
Знания
Что такое тригонометрическое уравнение?
Понимание
Какая разница между простейшим уравнение и записанным?
Сделайте одно «сложное» уравнение из двух простых.
Применение
Решите два простых уравнения
Решите записанное усложненное
Анализ
Назовите, как создаются «усложненные » уравнения
Сравните несколько таких уравнений. Назовите усложнения
Синтез
Напишите 3 уравнения, составленные по найденным схемам
Решите их
Оценка
Поменяйтесь тетрадями с соседом по парте и определите,
правильно ли ваш сосед понимает решение уравнений, и приготовьтесь ответить на вопросы.
Слайд 7 Уравнение касательной к графику функции
Геометрический смысл
производной состоит в том, что значение производной функции
f (x) в точке x равно угловому коэффициенту касательной к графику функции в точке (x;f(x)).
f '(x) = k = tg φ
Уравнение касательной записывается в виде:
y = f (x0) + f ' (x0) · (x-x0) ,
где x0 - абсцисса заданной точки.
f (x) в точке x равно угловому коэффициенту касательной к графику функции в точке (x;f(x)).
f '(x) = k = tg φ
Уравнение касательной записывается в виде:
y = f (x0) + f ' (x0) · (x-x0) ,
где x0 - абсцисса заданной точки.
Слайд 8Задание: Написать уравнение касательной к графику функции f( x ) = x2
+ x +1 в точке с абсциссой x0 = 1
Вопросы .
Анализ.
Опишите своими словами, что вы понимаете под касательной?
Сколько точек соприкосновения может быть у касательной и графика функции?
Попробуйте сделать эскиз произвольного графика функции и провести касательную в какой-либо точке графика.
Посмотрите на уравнение касательной. Какие составляющие вы видите в этом уравнении?
Давайте составим алгоритм для написания уравнения касательной.
Слайд 9
Уравнение касательной: y = f (x0) + f ' (x0) ·
(x-x0) ,
где x0 - абсцисса заданной точки.
Алгоритм
Найти f( x0) ;
Найти f ' (x) ;
Найти f ' (x0) .
Составим уравнение касательной y = kx + b
f ( x0) = 12+1+1=3
f ' (x) = 2x+1
f ' (x0) = 2·1+1=3
y = 3+3·( x-1) = 3+3x-3 = 3x
где x0 - абсцисса заданной точки.
Алгоритм
Найти f( x0) ;
Найти f ' (x) ;
Найти f ' (x0) .
Составим уравнение касательной y = kx + b
f ( x0) = 12+1+1=3
f ' (x) = 2x+1
f ' (x0) = 2·1+1=3
y = 3+3·( x-1) = 3+3x-3 = 3x
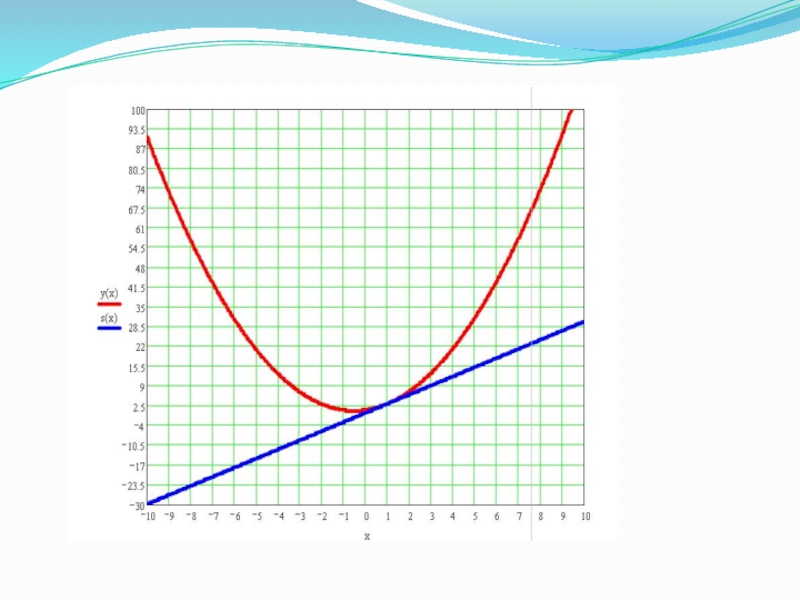
Слайд 10Синтез.
Проверим правильность выполненной задачи: постройте данную прямую.
Сколько точек потребуется для построения
прямой ? (аксиома планиметрии).