- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Путешествие в историю математики
Содержание
- 1. Презентация по математике Путешествие в историю математики
- 2. СодержаниеПериоды развития математикиТест по истории математикиВикторинаСтаринные задачиВысказывания о математике
- 3. Периоды развития математикиПериод зарождения математики (7-5 в.
- 4. Период зарождения математики начался с древних времен
- 5. Математика в Древнем Вавилоне
- 6. Математика в древнем Египте
- 7. Наши познания о математике древних цивилизаций основаны
- 8. Задача из папируса АхмесаПриходит пастух с 70
- 9. Математика Древней Греции
- 10. Созданный Фалесом метод логического
- 11. Пифагор (ок. 585-500 до н.э.)
- 12. Достижения пифагорейцев1. Пифагорейцы предложили
- 13. Теорема Пифагора Пифагору и его
- 14. С помощью теоремы Пифагора решите задачу индийского
- 15. Большой вклад в развитие математики внесли также
- 16. Около 300 лет до н. э. результаты
- 17. Евклид Евклид жил около 300
- 18. Диофант Александрийский Диофанта (250 г. до н.
- 19. Узнай, сколько лет прожил Диофант, если на
- 20. Упадок Греции После завоевания Египта
- 21. Математика в древней Индии
- 22. Математика арабов
- 23. Достижения Арабской математики
- 24. Средневековая Европа В Европе, после
- 25. Изобретение книгопечатания Однако
- 26. Математика Эпохи Возрождения
- 27. Леонардо да Винчи(1452 - 1519)
- 28. Достижения итальянских математиков
- 29. Возникновение математической символики Но
- 30. Математика 17 века Принято
- 31. Рене Декарт Другой великий
- 32. Пьер Ферма Большой
- 33. Ньютонова революция в науке
- 34. Математика 18 века 18
- 35. Леонард Эйлер (1707 -1783) Почти
- 36. Математика 19 векаВ 19 веке объектами математического
- 37. Карл Гаусс (1777 – 1855)Гаусса нередко называют
- 38. Геометрия в 19 векеЕсли 18 век был
- 39. Современная математикаЕсли математику, известную до 1600, можно
- 40. Слайд 40
- 41. Слайд 41
- 42. Тест по истории
- 43. 9.. Кто из великих древнегреческих математиков вычислил
- 44. Назовите терминЭто термин происходит от латинских слов
- 45. Старинные задачиЗадачи индийских математиковЗадачи из учебника Магницкого
- 46. Евклид
- 47. Леонтий Филиппович Магницкий
- 48. Софья Ковалевская
- 49. Леонардо да Винчи
- 50. Франсуа Виет
- 51. Николай Лобачевский
- 52. От имени ученого – Аль-Хорезми произошло слово алгоритм; от названия его работы – «Аль-джебр…» слово алгебра.
- 53. Ответ к задаче о пастухе: в стаде 315 быков
- 54. Леонард ЭйлерЭйлер положил основания теории функций комплексного
- 55. Первой среди научных и философских школ древней
- 56. Другим великим греком, с чьим именем связывают
- 57. Одним из самых выдающихся пифагорейцев был Платон
- 58. В 1508 году по приглашению папы Юлия
- 59. Франсуа Виет
- 60. Ответы к слайду «Назовите математика»ЕвклидСофья КовалевскаяЛеонардо да ВинчиФрансуа ВиетНиколай ЛобачевскийЛеонтий Магницкий
- 61. Ответы к слайду «Назовите термин»БиссектрисаРадиусКубГипотенузаПропорцияПравильные многогранники: тетраэдр, гексаэдр, октаэдр, икосаэдр, додекаэдр.
- 62. Высказывания о математикеМатематику уже затем учить надо,
- 63. Задачи индийских математиковВ древней Индии были распространены
- 64. Задачи индийского ученого 12 века БхаскарыОбезьянок резвых
- 65. Задача о лотосе Из множества
- 66. Задача о тополеНа берегу реки рос тополь
- 67. Первый русский учебник арифметикиВ 1701 году по
- 68. Задачи из «Арифметики» Магницкого Случися некоему
- 69. Задача про учеников Отец
- 70. Задача о плотнике Некий господин
- 71. Ответ к задаче про обезьянок: 16 или 48 обезьянок было в стае.
Слайд 1Путешествие в историю математики
Автор: учитель математики МБОУ гимназии №1
Г. Миллерово
Попова Галина Владимировна
Слайд 2Содержание
Периоды развития математики
Тест по истории математики
Викторина
Старинные задачи
Высказывания о математике
Слайд 3Периоды развития математики
Период зарождения математики
(7-5 в. до н.э.)
Период элементарной математики
Период математики переменных величин (17 - 18 в.)
Период современной математики
(19 - 20 в.)
Слайд 4Период зарождения математики начался с древних времен и закончился в VII-Vвв.
Это был период накопления фактического материала, связанного с потребностями хозяйственной жизни – развитием ремесла, земледелия, обмена и торговли, исчислением податей, измерением площадей земельных участков, объемов сосудов и т. д.
Слайд 5Математика в Древнем Вавилоне
Вавилоняне составили таблицы обратных
Деление окружности на 360, а градуса и минуты на 60 частей берут начало в вавилонской астрономии.
Слайд 6Математика в древнем Египте
Египтяне могли выполнять действия
Слайд 7Наши познания о математике древних цивилизаций основаны главным образом на двух
Математический папирус Ахмеса
(также известен как папирус Ринда) — древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства, переписанное ок. 1650 до н. э. писцом по имени Ахмес на свиток папируса длиной 5,25 м. и шириной 33 см.
Папирус Ахмеса включает условия и решения 84 задач прикладного характера.
Московский математический папирус, находящийся в Государственном музее изобразительных искусств имени А. С. Пушкина, уступает папирусу Ахмеса по полноте (он состоит из 25 задач), но, вероятно, превосходит по возрасту.
Слайд 8Задача из папируса Ахмеса
Приходит пастух с 70 быками. Его спрашивают:
-Сколько приводишь
Пастух отвечает:
-Я привожу две трети от трети скота. Сочти!
Сколько быков в стаде?
Ответ
Слайд 9Математика Древней Греции
Древнеегипетскую и вавилонскую культуру
Основным достижением математической мысли было возникновение и развитие понятия о доказательстве.
Первым из философов, применившим в математике «дедуктивный метод» называют греческого ученого Фалеса, жившего в VII-VI вв до нашей эры. По дошедшим до нас сведениям, Фалес доказал некоторые простейшие геометрические утверждения: равенство углов при основании равнобедренного треугольника, равенство вертикальных углов.
Подробнее.
Слайд 10
Созданный Фалесом метод логического доказательства был развит и
По легенде за доказательство этой теоремы ученый принес в жертву богам 100 быков.
Назовите его имя.
Слайд 11Пифагор (ок. 585-500 до н.э.)
С именем Пифагора
Слайд 12Достижения пифагорейцев
1. Пифагорейцы предложили разнообразные классификации целых чисел:
простые, составные
совершенные, дружественные и т.д.
2. Развили теорию отношений и пропорций
Доказали некоторые свойства правильных многоугольников
Пифагор и его ученики считали, что с помощью чисел можно выразить все закономерности мира, что они являлись основой всех вещей и явлений природы.
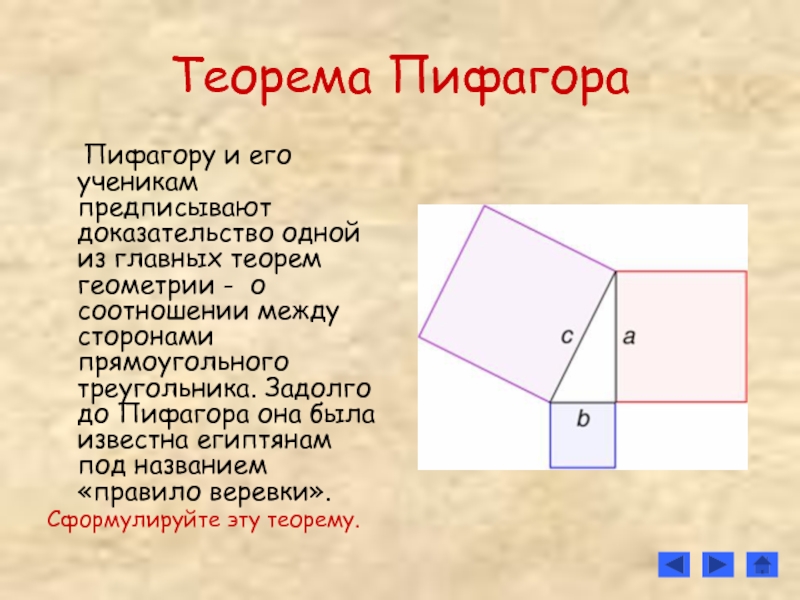
Слайд 13Теорема Пифагора
Пифагору и его ученикам предписывают доказательство одной
Сформулируйте эту теорему.
Слайд 14С помощью теоремы Пифагора решите задачу индийского математика XII в. Бхаскары
Над озером тихим
С пол фута размером,
Высился лотоса цвет
Он рос одиноко.
И ветер порывом
Отнес его в сторону.
Нет боле цветка над водой,
Нашел же рыбак его
ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока?
Слайд 15Большой вклад в развитие математики внесли также следующие древнегреческие ученые
Платон (427-347
Евдокс (408-355 до н. э.) – ввел понятие величины, «метод исчерпывания».
Аристотель – заложил основы науки логики и высказал идеи относительно определений, аксиом, бесконечности.
Архимед (ок. 287 до н.э.) – разработал методы нахождения площадей поверхностей и объемов тел. Подробнее.
Слайд 16Около 300 лет до н. э. результаты многих греческих математиков были
Слайд 17Евклид
Евклид жил около 300 г. до нашей эры
Слайд 18Диофант Александрийский
Диофанта (250 г. до н. э.) называют «отцом алгебры».
Он ввел обозначение неизвестных величин, их степеней, знаки для вычитания и равенства. Впервые в его трудах появились отрицательные числа.
Он разработал общие методы решения линейных и квадратных уравнений.
Слайд 19Узнай, сколько лет прожил Диофант, если на его могиле высечена надпись:
Путник!
И числа поведать могут, о чудо, сколь долог был век его жизни.
Часть шестую его представляло прекрасное детство.
Двенадцатая часть протекла еще жизни – покрылся пухом тогда подбородок
Седьмую в бездетном браке провел Диофант.
Прошло пятилетие; он был осчастливлен рожденьем прекрасного первенца сына,
Коему рок половину лишь жизни прекрасной и светлой дал на земле по сравненью с отцом.
И в печали глубокой старец земного удела конец воспринял, переживши года четыре с тех пор, как сына лишился.
Слайд 20Упадок Греции
После завоевания Египта римлянами в 31 г.
Слайд 21Математика в древней Индии
Индийские математики впервые
Арабские числа стали известны европейцам в X—XIII вв. благодаря их изображениям на косточках абака. Для экономии места они изображались боком. Поэтому, в частности, цифры «2» и «3» приобрели ту форму, которую мы знаем.
Слайд 22Математика арабов
В 7-8
Арабские математики изучили и перевели труды ученых Греции, Индии, Китая и благодаря их комментариям Европа также познакомилась с великими творениями ученых древности.
Слайд 23Достижения Арабской математики
Наибольших
Главная книга Хорезми названа скромно: "Учение о переносах и сокращениях", то есть техника решения алгебраических уравнений. По арабски это звучит "Ильм аль-джебр ва"ль-мукабала»
Какие термины произошли от имени ученого и названия его книги?
Ответ
Слайд 24Средневековая Европа
В Европе, после распада Римской империи наступили
Однако всему приходит конец – даже темным векам. Около 1100 г. в западноевропейской математике начался почти трехвековой период освоения сохраненного арабами и византийскими греками наследия Древней Греции и Востока. Первым, заслуживающим упоминания европейским математиком стал Леонардо Пизанский (Фибоначчи). В своем сочинении Книга абака (1202) он познакомил европейцев с индо-арабскими цифрами и методами вычислений, а также с арабской алгеброй.
Слайд 25Изобретение книгопечатания
Однако решающий прорыв из Средневековья
В 1482 году в Венеции была впервые напечатана (по латыни) книга Евклида "Начала". С этого момента для математиков кончилось Средневековье и началось Новое время.
Слайд 26Математика Эпохи Возрождения
Когда распространилось книгопечатание, каждый
Итальянские художники 15 века научились применять стереометрию в живописи. Они изобрели технику перспективы, благодаря которой плоские изображения пространственных тел кажутся неотличимы от реальных предметов.
Назовите имя художника, который особенно отличился в этой области.
Слайд 27Леонардо да Винчи(1452 - 1519)
Следуя по стопам
Слайд 28Достижения итальянских математиков
В 16 в
На них математики предлагали коллегам решить различные алгебраические задачи. Итогом таких турниров, стало открытие приемов и способов решения уравнений 3 и 4 степени.
Эти открытия были опубликованы в 1545 г. Джироламо Кардано в книге «Великое искусство».
Предложите задачу для команды соперников.
Слайд 29Возникновение математической символики
Но решения уравнений сопровождались затруднениями,
В алгебре эту проблему удачно решил французский математик. Он впервые использовал привычные нам знаки арифметических действий над известными числами или над буквами, изображающими неизвестные числа. Изложив на этом языке все известные факты о решении уравнений – многочленов, математик заметил связь между коэффициентами и корнями этих уравнений.
Кто этот математик?
Ответ.
Слайд 30Математика 17 века
Принято считать, что вся современная
Одним из замечательных ученых этого периода был немец Иоганн Кеплер (1571 – 1630).
С 1600 г. он работал в Пражской обсерватории наблюдал за движением планет. Успехи Кеплера в расчете пройденного планетой пути по известной скорости движения стали первым шагом в новой науке – интегральном исчислении.
Слайд 31Рене Декарт
Другой великий математик – француз Рене
Двухсторонний «словарь» переводящий фразы одного из этих языков в равнозначные фразы другого языка, Декарт назвал аналитической геометрией.
Слайд 32Пьер Ферма
Большой вклад в создание аналитической
По основной профессии он был юрист, а математикой занимался на досуге. Ферма ни в одной области науки не был первым. В математический анализ он вошел вслед за Архимедом и Кеплером, в аналитическую геометрию - вслед за Декартом, в теорию вероятностей - вслед за Паскалем, в теорию чисел - вслед за Диофантом. Но в каждом случае Ферма добавлял в уже готовую или только рождающуюся науку столь важные открытия, что превзойти его результаты могли только гении - порою много десятилетий спустя.
Слайд 33Ньютонова революция в науке
Так математики и
Почти всех математиков того времени привлекала задача определения и вычисления мгновенных скоростей различных величин.
Независимо друг от друга решение этой задачи дали англичанин И.Ньютон и немец Готфрид Лейбниц. Они стали основоположниками методов математического анализа: дифференциального и интегрального исчисления.
Слайд 34Математика 18 века
18 век в математике стал
Главным методом познания природы становится составление и решение дифференциальных уравнений. Центрами математических исследований остаются Академии наук. Математики становятся профессионалами, любители почти исчезают со сцены.
C точки зрения математики, 18 век можно назвать веком Эйлера. Его гигантская фигура накладывает отпечаток на все математические достижения столетия. Именно он сделал из анализа совершенный инструмент исследования.
Слайд 35Леонард Эйлер (1707 -1783)
Почти полжизни Эйлер провёл в
Научное наследие Леонарда Эйлера колоссально. Эйлеру принадлежит знаменитый шеститомный курс математического анализа на котором учились многие поколения математиков всего мира. Подробнее.
Слайд 36Математика 19 века
В 19 веке объектами математического исследования всё больше становятся
Были созданы новые математические теории: теория вероятностей, теория чисел, теория пределов, теория множеств и другие.
Слайд 37Карл Гаусс (1777 – 1855)
Гаусса нередко называют наследником Эйлера. Они оба
Математический талант Гаусса проявился в раннем детстве и конечно, первым его увлечением стала арифметика. В 9 лет он открыл (во время школьного урока) формулу суммы арифметической прогрессии.
К. Гаусс создал основы теории чисел, развил арифметику комплексных чисел, и т. д.
Слайд 38Геометрия в 19 веке
Если 18 век был веком анализа, то 19-й
Слайд 39Современная математика
Если математику, известную до 1600, можно охарактеризовать как элементарную, то
Слайд 40 Назовите имя математика
1. Одна из легенд об этом математике рассказывает, что царь Птолемей обратился к нему с вопросом, нет ли более легкого пути к познанию его трудов, на что ученый гордо ответил: «К геометрии нет царской дороги!».
Кто он?
Ее знакомство с математикой произошло в 8 лет, так как стены ее комнаты были оклеены листами с записями лекций по математике профессора Островского. Кто она?
3. В 1700 г. Петром I он был учинен «российскому благородному юношеству» учителем математики. Им был создан первый русский учебник математики, который Ломоносов называл «вратами учености». В знак признательности царь Петр пожаловал ему другую фамилию. Кто он?
Слайд 41
4. «Пусть
5. Во время войны Франции с Испанией вся тайная переписка испанцев свободно читалась французами, так как этот математик всякий раз разгадывал испанский шифр, как бы его не запутывали вражеские шифровальщики. Не представляя себе могущества человеческого ума, испанцы думали, что французам помогает дьявол. Они даже жаловались римскому папе и просили его уничтожить эту “дьявольскую силу”. Кто он?
6. Труды этого русского математика не были признаны при его жизни, т.к. в них он подробно излагал геометрию, основанную на новой аксиоме о параллельных, согласно которой через точку, лежащую в данной плоскости вне данной прямой, можно провести по крайней мере две прямые, не пересекающие заданную прямую. Кто он?
Слайд 42 Тест по истории математики
В какой стране родился
[Египет; Древняя Греция; Древний Рим.]
2. Кто из математиков, родившись в Швейцарии, всю свою жизнь и талант отдал служению России? [Виет; Эйлер; Лейбниц.]
3. В каком древнегреческом городе занимался научной деятельностью Евклид? [Эфес; Александрия; Афины.]
4. Какой знаменитый ученый-математик впервые ввел переменную величину? [Лейбниц; Декарт; Ферма.]
5. Какой знаменитый человек, своеобразный «титан» эпохи Возрождения, фантастически разносторонняя и талантливая личность, ввел в математику знаки «+» и «–»?
[Дюрер; Леонардо да Винчи; Микеланджело.]
6. Какая геометрическая фигура обязана своим названием греческому столику для еды? [Трапеция; ромб; квадрат.]
7. Какое геометрическое тело обязано своим названием лесной шишке?
[Пирамида; конус; шар.]
8. Какой русский писатель любил сочинять задачи для маленьких детей?
[Н. Гоголь; Л. Толстой; М. Лермонтов.]
Слайд 43
9.. Кто из великих древнегреческих математиков вычислил отношение длины окружности к
[Архимед; Пифагор; Евклид.]
10. Кто из великих математиков ввел правило нахождения экстремума с помощью производной? [Эйлер; Ферма; Лобачевский.]
11. Кто из знаменитых математиков впервые ввел понятие «функция»?
[Лейбниц; Гаусс; Лиувилль.]
12. Кто из ученых-математиков впервые в XVI в. ввел формулу для решения кубического уравнения? [Гаусс; Виет; Тарталья.]
13. Математик, давший доказательство основной теоремы алгебры (всякое алгебраическое уравнение с действительными коэффициентами имеет корень). [Гаусс; Кардано; Галуа.]
14. Древнегреческий философ, являющийся одним из основателей логического метода рассуждения «от противного».
[Платон; Птолемей; Анаксагор.]
15. Русский математик и педагог, создатель учебной книги по математике, на которой воспитывалось не одно поколение школьников. [Осиповский; Ломоносов; Магницкий.]
16. Создатель неевклидовой геометрии. [Лобачевский; Фалес; Эйлер.]
Слайд 44Назовите термин
Это термин происходит от латинских слов «дважды» и «секу». О
Этот термин ввел Франсуа Виет, в переводе с латинского он означает «спица колеса». Что это?
Этот термин ввели пифагорейцы, а название произошло от греческого слова, означающего в переводе «игральная кость». Что это?
Этот термин в переводится с греческого, как «натянутая тетива». Назовите его.
Это понятие было в большом почете у пифагорейцев, с ним они связывали мысли о порядке и красоте в природе. Оно применяется не только в математике, но и в искусстве, архитектуре. Что это?
Считалось, что формы этих платоновых тел, присущи элементам первооснов бытия, а именно: огню, земле, воздуху, воде, вселенной. О чем идет речь?
Ответы.
Слайд 52От имени ученого – Аль-Хорезми произошло слово алгоритм; от названия его работы
Слайд 54Леонард Эйлер
Эйлер положил основания теории функций комплексного переменного, теории обыкновенных дифференциальных
Эйлер внес большой вклад в алгебру и теорию чисел, где его результаты являются классическими и известны в науке под названием формул и теорем Эйлера.
Используя специально подобранную символику, Эйлер облегчил язык математики, сделал ее более обозримой и более доступной. Он, например, ввел сокращенные обозначения тригонометрических функций угла х: tg x, ctg x, sec x, cosec x (обозначения sin x и cos x : были введены И. Бернулли).
Эйлер установил современную точку зрения на тригонометрические функции как функции числового аргумента. В трудах Эйлера тригонометрия приняла тот вид, который она имеет в настоящее время.
Математические методы Эйлер распространил и на другие науки (оптика, теория музыки, баллистика, морская наука, страховое дело и т. д.).
Характерной особенностью всех трудов Эйлера является конкретная постановка математических проблем и задач, требующих развития новых методов, стремление получить решение задач в виде законченных формул, по которым желаемый ответ находится с любой степенью точности.
Лаплас назвал Эйлера общим учителем всех математиков второй половины XVIII века. К этому надо добавить, что Эйлер явился идейным предшественником многих математиков XIX и XX веков.
Слайд 55
Первой среди научных и философских школ древней Греции была ионийская (VI
Представителем новой формы рационального мышления в математике, основателем ионийской школы считается Фалес Милетский (640 - 548 г.г. до н.э.). Во время путешествий он посетил Египет, где и познакомился с астрономией и геометрией. Легенда рассказывает о том, что Фалес привел в изумление египетского царя Амазиса, измерив высоту одной из пирамид по величине отбрасываемой ею тени (рис. 6). Задача. Измерить высоту пирамиды по отбрасываемой ею тени. (Размеры даны в локтях; 1 локоть = 7 ладоням = 466 мм.) В геометрии ему приписывают ряд утверждений. Вот первое из них: "Диаметр делит окружность (круг) пополам". Доказательством служил рисунок - круг, разделенный на равные секторы. Он обосновал также и другие: "Углы при основании равнобедренного треугольника равны", второй признак равенства треугольников. Фалес мыслил углы не как величины, а как фигуры, имеющие некоторую форму.
В этой школе был введен процесс обоснования как необходимый компонент математической деятельности, что являлось отличительной чертой их математики. Свое существование школа прекратила после падения Милета, завоеванного персами в 494 году до н. э. Дальнейшее развитие математики происходило в другой древнегреческой школе, основателем которой был легендарный Пифагор (564-473 г.г. до н. э.).
Слайд 56
Другим великим греком, с чьим именем связывают развитие математики, был Пифагор
Из простых геометрических конфигураций возникали некоторые свойства целых чисел. Например, пифагорейцы обнаружили, что сумма двух последовательных треугольных чисел всегда равна некоторому квадратному числу. Они открыли, что если (в современных обозначениях) n2 – квадратное число, то n2 + 2n +1 = (n + 1)2. Число, равное сумме всех своих собственных делителей, кроме самого этого числа, пифагорейцы называли совершенным. Примерами совершенных чисел могут служить такие целые числа, как 6, 28 и 496. Два числа пифагорейцы называли дружественными, если каждое из чисел равно сумме делителей другого; например, 220 и 284 – дружественные числа (и здесь само число исключается из собственных делителей).
Слайд 57
Одним из самых выдающихся пифагорейцев был Платон (ок. 427–347 до н.э.).
Величайшим из греческих математиков классического периода, уступавшим по значимости полученных результатов только Архимеду, был Евдокс (ок. 408–355 до н.э.). Именно он ввел понятие величины для таких объектов, как отрезки прямых и углы. Располагая понятием величины, Евдокс логически строго обосновал пифагорейский метод обращения с иррациональными числами.
Работы Евдокса позволили установить дедуктивную структуру математики на основе явно формулируемых аксиом. Ему же принадлежит и первый шаг в создании математического анализа, поскольку именно он изобрел метод вычисления площадей и объемов, получивший название «метода исчерпывания». Этот метод состоит в построении вписанных и описанных плоских фигур или пространственных тел, которые заполняют («исчерпывают») площадь или объем той фигуры или того тела, которое является предметом исследования. Евдоксу же принадлежит и первая астрономическая теория, объясняющая наблюдаемое движение планет. Предложенная Евдоксом теория была чисто математической; она показывала, каким образом комбинации вращающихся сфер с различными радиусами и осями вращения могут объяснить кажущиеся нерегулярными движения Солнца, Луны и планет.
Слайд 58
В 1508 году по приглашению папы Юлия II Рафаэль отправляется в
Фреска «Афинская школа» воплощает величие философии и науки. Ее основная идея — возможность гармонического согласия между различными направлениями философии и науки — принадлежит к числу важнейших идей гуманистов. Под сводами величественного здания расположились группами древнегреческие философы и ученые.
В центре композиции находятся Платон и Аристотель, олицетворяющие античную мудрость и представляющие две школы философии. Платон указывает пальцем на небо, Аристотель простирает руку над землей. Воин в шлеме — Александр Македонский, он внимательно слушает Сократа, который, что-то доказывая, загибает пальцы. Слева, у подножия лестницы, Пифагор, в окружении учеников, занят разработкой математических проблем. Человек в венке из виноградных листьев — Эпикур. Человек, сидящий в задумчивой позе, опершись на куб, — Микеланджело в образе Гераклита. На ступеньках лестницы расположился Диоген. Справа Евклид, склонясь над доской, измеряет циркулем геометрический чертеж. Ступени лестницы символизируют этапы овладения истиной. Рядом с Евклидом стоят Птолемей (держит в руках земной шар) и, вероятно, пророк Зороастр (держит небесный глобус). Чуть правее стоит сам художник (смотрит прямо на зрителя). Хотя на фреске представлено свыше 50 фигур, свойственное Рафаэлю чувство пропорций и ритма создает впечатление удивительной легкости и простора.
Слайд 60Ответы к слайду «Назовите математика»
Евклид
Софья Ковалевская
Леонардо да Винчи
Франсуа Виет
Николай Лобачевский
Леонтий Магницкий
Слайд 61Ответы к слайду «Назовите термин»
Биссектриса
Радиус
Куб
Гипотенуза
Пропорция
Правильные многогранники: тетраэдр, гексаэдр, октаэдр, икосаэдр, додекаэдр.
Слайд 62Высказывания о математике
Математику уже затем учить надо, что она ум в
Математика представляет искуснейшие изобретения, способные удовлетворить любознательность, облегчить ремесла и уменьшить труд людей. Декарт Р.
Математика – первая из всех наук и полезна, и необходима для них. Бэкон Р.
Математика – царица наук, арифметика – царица математики. К. Гаусс
Математику нельзя изучать, наблюдая, как это делает сосед! А. Нивен
Слайд 63Задачи индийских математиков
В древней Индии были распространены публичные соревнования в решении
Слайд 64Задачи индийского ученого 12 века Бхаскары
Обезьянок резвых стая
Всласть поевши развлекалась
Их в
На поляне забавлялась.
А двенадцать по лианам…
Стали прыгать, повисая.
Сколько было обезьянок,
Ты скажи мне, в этой стае?
(Задача на составление квадратного уравнения)
Ответ.
Слайд 65Задача о лотосе
Из множества чистых цветков лотоса были
Четвертую долю получил Бхавани, а остальные шесть цветков получил уважаемый учитель. Сколько было цветков?
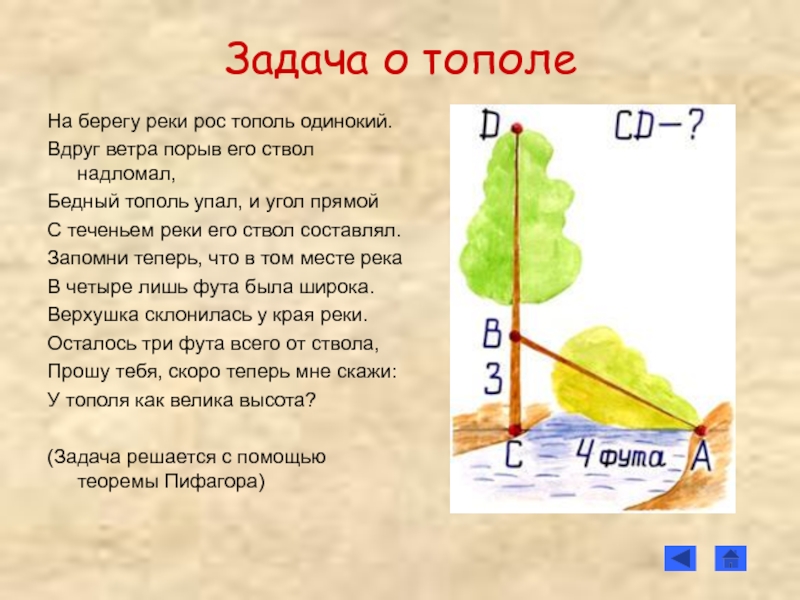
Слайд 66Задача о тополе
На берегу реки рос тополь одинокий.
Вдруг ветра порыв его
Бедный тополь упал, и угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
(Задача решается с помощью теоремы Пифагора)
Слайд 67Первый русский учебник арифметики
В 1701 году по приказу ПетраI в Москве
Одним из преподавателей в этой школе был Леонтий Филиппович Магницкий, который в 1703 году опубликовал книгу «Арифметика сиречь наука числительная».
Эта книга является первым фундаментальным трудом в истории русской математики, на ней училось и воспитывалось не одно поколение россиян.
Слайд 68Задачи из «Арифметики» Магницкого
Случися некоему человеку к стене лествицу
Слайд 69Задача про учеников
Отец решил отдать сына
Слайд 70Задача о плотнике
Некий господин позвал плотника и велел