- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике: Проценты
Содержание
- 1. Презентация по математике: Проценты
- 2. Опережающее обучениеПонять- значит, привыкнуть и
- 3. Как сделать понятным тот или иной материал?
- 4. Именно привыкания к пользованию часто не хватает
- 5. Десятичные дроби начинаем изучать в феврале, а
- 6. Во многих школьных учебниках десятичные дроби излагаются
- 7. Десятичные меры длины.Метр- единицаДециметр-десятаяСантиметр- сотаяМиллиметр-тысячная
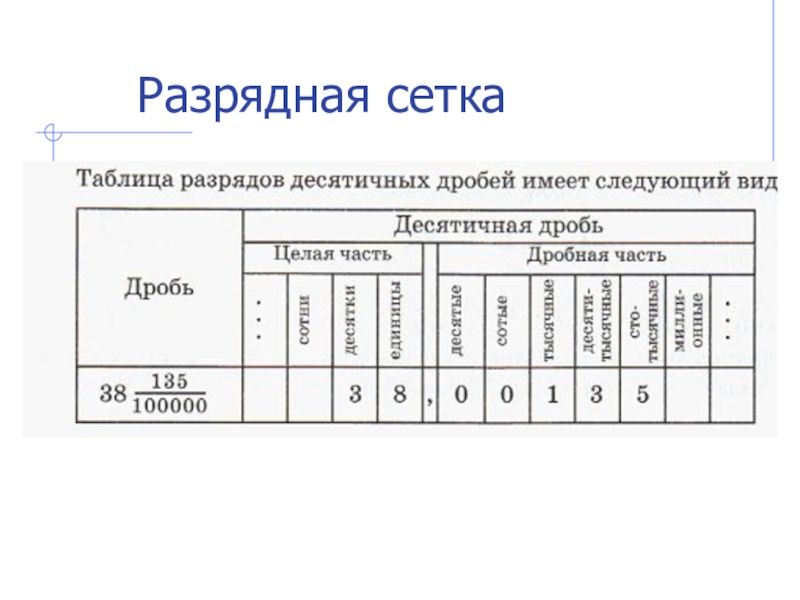
- 8. Разрядная сетка
- 9. Важные свойства разрядной сетки: цифра, стоящая в
- 10. Работаем мы в одном и том же
- 11. Задача №1 В этой таблице записаны результаты измерения веревки. Запишите длину этой веревки в миллиметрах.
- 12. Задача №2Длина ленты 2м 4дм 3см 5мм. Запишите эти данные в таблицу:
- 13. Задача № 18Десятичные дроби складываются так же,
- 14. Решите числовые ребусыЗадача №29.УДА,Р +УДА,Р = ДРАК,А
- 15. Понятие процентаЯ процент, - раздался крик, - Заявляю сразу:В школе каждый ученикЗнать меня обязан!
- 16. Процент…Процент –
- 17. Задача №1Один процент от числа – это
- 18. Виды рассматриваемых задач:1.Задачи на нахождение процента от
- 19. Задачи на простыепроцентыНахождение процентов от числа.Нахождение числа
- 20. Задача: Сколько процентов соли содержит раствор,
- 21. Закон сохранения массы сухого веществаВ задачах о
- 22. Задача.. Виноград содержит 90% влаги, а изюм
- 23. Виноград Х кгВлажность 90%Сухое вещество 10%Изюм 20 кгВлажность 5%Сухое вещество 95%20кг. –
- 24. Задача. Виноград содержит 90% влаги, а изюм
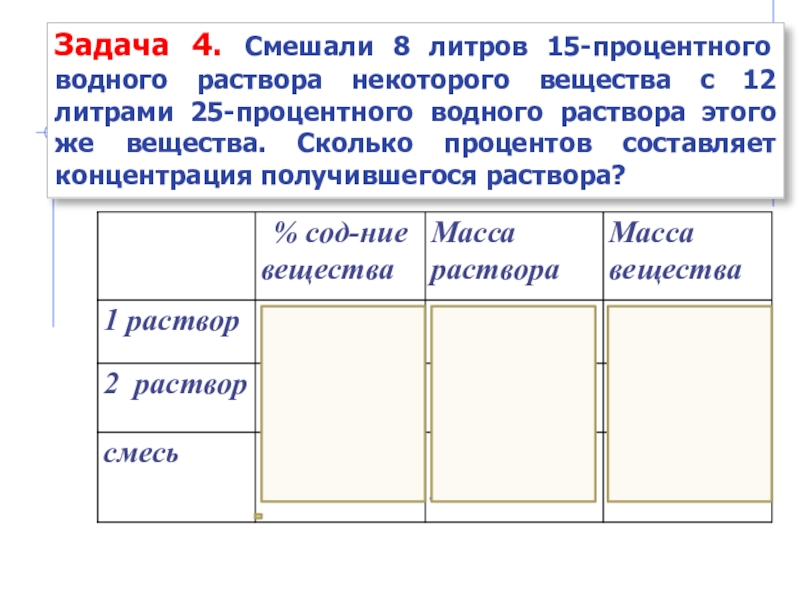
- 25. Задача 4. Смешали 8 литров 15-процентного водного
- 26. 20 x = 8 ▪ 0,15 +
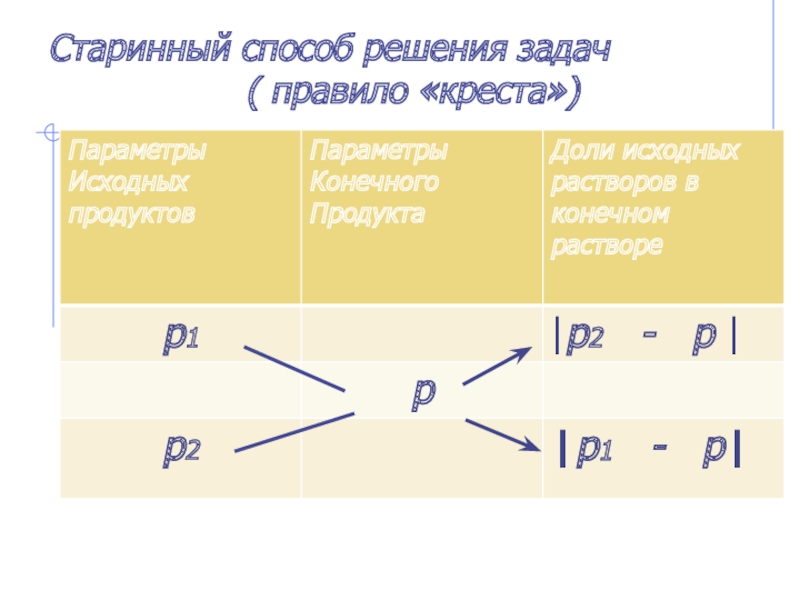
- 27. Старинный способ решения задач( правило «креста»)
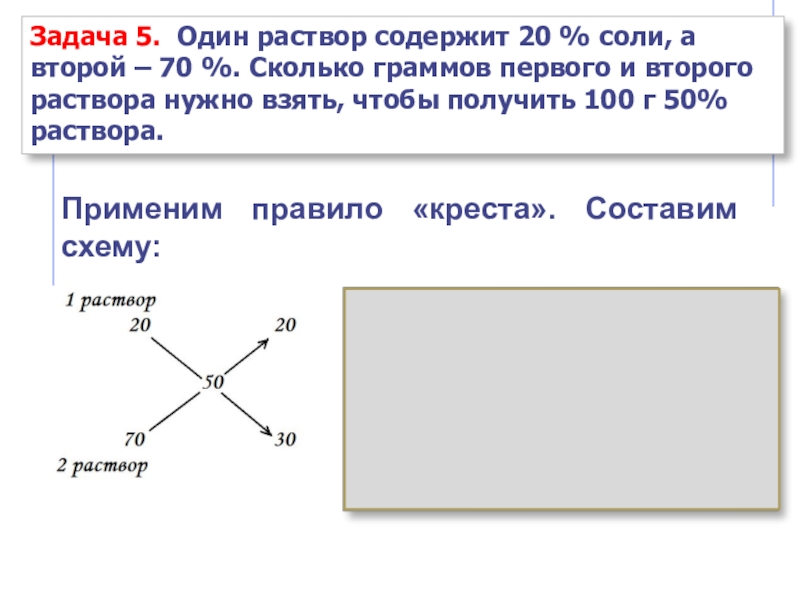
- 28. Задача 5. Один раствор содержит 20 %
- 29. Задача 6. Первый сплав содержит 10 %
- 30. х ∙ 0,1 + у ∙
- 31. х ∙ 0,1 + ( 3
- 32. 3 способ. Правило «креста»
- 33. 30 кг(30-x)кгХкг+=10%25% 20%10Х+(30-Х)=30*20Ответ : 1 сплав
- 34. Подготовка к ОГЭ и ЕГЭ
- 35. «Я могу только показать тебе дверь, войти
- 36. Простейшие задачи, связанные с понятием проценты. Простой процентный рост.
- 37. Слайд 37
- 38. Необходимо знать!
- 39. 1. Хр. – 100% Ур. –
- 40. По данным исследований в памяти человека остаётся
Слайд 3Как сделать понятным тот или иной материал? А вот так: сделать
Слайд 4Именно привыкания к пользованию часто не хватает нашему школьнику для понимания
Слайд 5Десятичные дроби начинаем изучать в феврале, а мае пишем по ним
Слайд 6Во многих школьных учебниках десятичные дроби излагаются в 5 классе во
Н.Я. Виленкина самом распространенном в России.
Слайд 9Важные свойства разрядной сетки:
цифра, стоящая в каком- либо ее столбце,
ее ограниченность справа при неограниченности слева.
Слайд 10Работаем мы в одном и том же режиме: в течение каждой
Слайд 11Задача №1
В этой таблице записаны результаты измерения веревки. Запишите
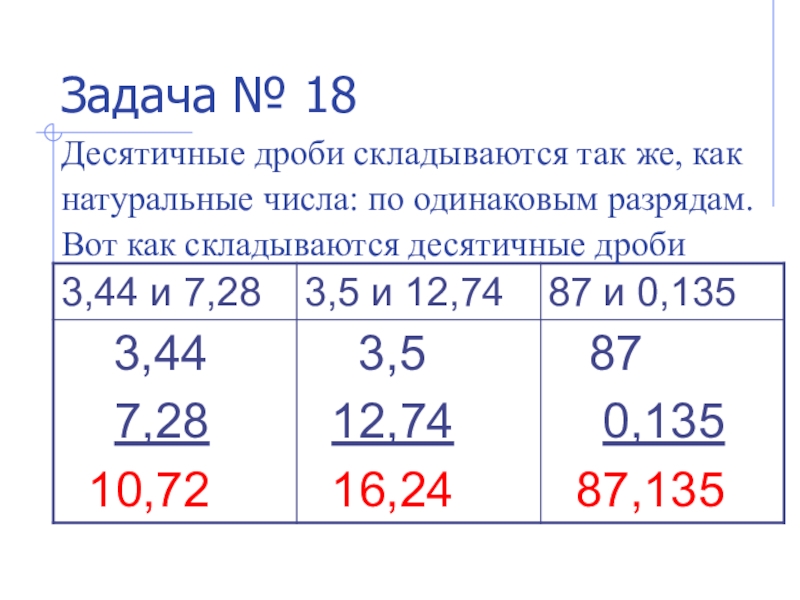
Слайд 13Задача № 18
Десятичные дроби складываются так же, как натуральные числа: по
Слайд 15Понятие процента
Я процент, - раздался крик, -
Заявляю сразу:
В школе каждый
Знать меня обязан!
Слайд 16 Процент…
Процент – это сотая часть любой
пути, массы, площади, количества, объёма …
Сотая часть метра – это … сантиметр
Сотая часть рубля … копейка
Сотая часть центнера … килограмм
Слайд 17Задача №1
Один процент от числа – это сотая часть. Например, один
Слайд 18Виды рассматриваемых задач:
1.Задачи на нахождение процента от числа;
2.Задачи на нахождение числа
3.Задачи на нахождение процентного отношения двух чисел.
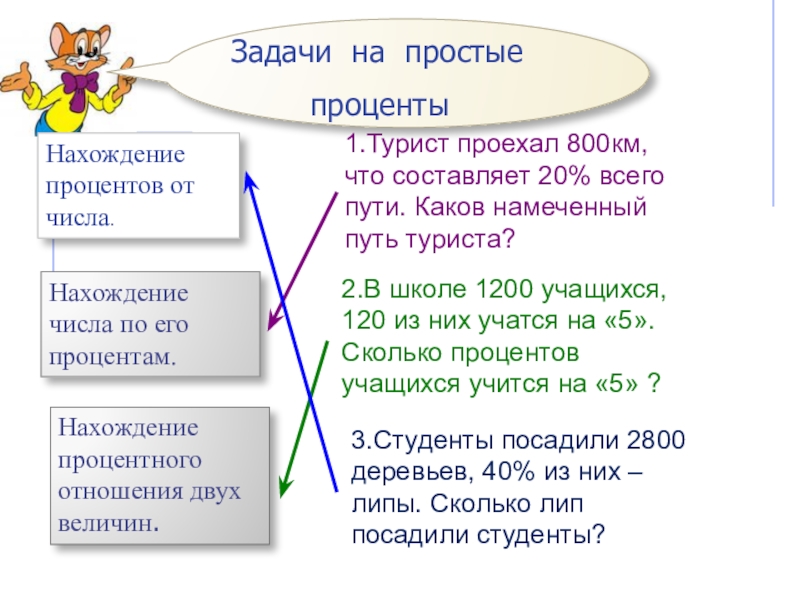
Слайд 19Задачи на простые
проценты
Нахождение процентов от числа.
Нахождение числа по его процентам.
Нахождение процентного
3.Студенты посадили 2800 деревьев, 40% из них – липы. Сколько лип посадили студенты?
1.Турист проехал 800км, что составляет 20% всего пути. Каков намеченный путь туриста?
2.В школе 1200 учащихся, 120 из них учатся на «5».
Сколько процентов учащихся учится на «5» ?
Слайд 20Задача: Сколько процентов соли содержит раствор, приготовленный из 35 г
Решение:
1)165 + 35 = 200 г – масса всего раствора
2) 200г - 100%
35г - ?
200 : 100 = 2г в 1%
35 : 2 = 17,5%
35г от 200г составляет 35 / 200.
35 / 200 *100= 35 : 200 *100 = 0,175 *100 = 17,5%
Ответ: 17,5%
1-й способ:
2-й способ:
Смеси, растворы, сплавы
Слайд 21Закон сохранения массы сухого вещества
В задачах о просушивании зерна, травы в
Концентрацию воды в этом продукте называют влажностью.
Ключевым моментом решения подобной задачи является использование закона сохранения массы сухого вещества в процессе просушивания рассматриваемого продукта.
В процессе просушивания продукта влажность изменяется, а сухое вещество остается прежним.
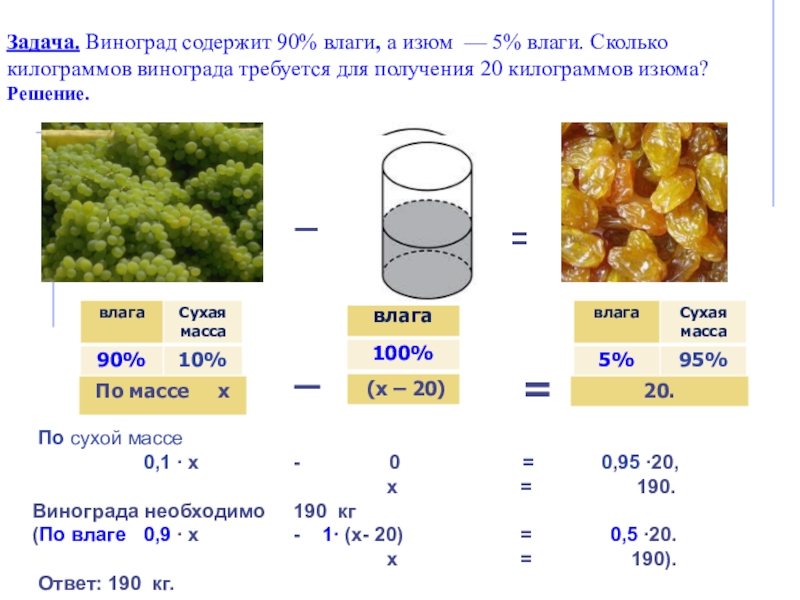
Слайд 22Задача.. Виноград содержит 90% влаги, а изюм — 5% влаги. Сколько
1.100-5=95(%) процентное содержание «сухого вещества» в изюме.
2. 20 :100•95=19(кг) масса «сухого вещества» в изюме
3. 100-90=10(%)процентное содержание «сухого вещества» в винограде
4. 19:10•100= 190 (кг) масса винограда
Ответ: 190 (кг) масса винограда
Слайд 23Виноград Х кг
Влажность 90%
Сухое вещество 10%
Изюм 20 кг
Влажность 5%
Сухое вещество 95%
20кг. – 100%:
У кг . -
У= 19 кг – сухого вещества содержится в 20 кг. изюма
2. Xкг. – 100%
19кг. – 10%
Х=190 кг
Ответ : для получения 20 кг. изюма требуется 190 кг винограда
Задача.. Виноград содержит 90% влаги, а изюм — 5% влаги. Сколько килограммов винограда требуется для получения 20 килограммов изюма?
Слайд 24Задача. Виноград содержит 90% влаги, а изюм — 5% влаги. Сколько
Решение.
_
=
_
=
По сухой массе
0,1 ∙ х - 0 = 0,95 ∙20,
х = 190.
Винограда необходимо 190 кг
(По влаге 0,9 ∙ х - 1∙ (х- 20) = 0,5 ∙20.
х = 190).
Ответ: 190 кг.
Слайд 25Задача 4. Смешали 8 литров 15-процентного водного раствора некоторого вещества с
Слайд 28Задача 5. Один раствор содержит 20 % соли, а второй –
.
100 г смеси составляют 20 + 30 = 50 частей.
100 : ( 20 + 30 ) = 2 г - на 1 часть.
2 ∙ 20 = 40 г – 20% раствора
2 ∙ 30 = 60 г – 70 % раствора
Ответ: 40 г- 20 % раствора; 60 г- 70 % раствора
Применим правило «креста». Составим схему:
Слайд 29Задача 6. Первый сплав содержит 10 % меди, второй -
Решить с помощью системы
Решить с помощью уравнения
Решить с помощью «креста»
Решить с помощью метода «стаканчиков»
Слайд 30
х ∙ 0,1 + у ∙ 0,25 = 3 *
х + у = 30
( 3 – у ) ∙ 0,1 + у ∙ 0,25 = 0,6
0,15 у = 0,3
у = 2 , значит х = 1.
Ответ : 1 сплав – 1 кг, 2 сплав – 2 кг.
( 3 – у ) ∙ 0,1 + у ∙ 0,25 = 0,6
х = 3 - у
Слайд 31
х ∙ 0,1 + ( 3 - х ) ∙
х ∙ 0,1 + 0,75 - х ∙ 0,25 = 0,6
- 0,15 х = - 0,15
х = 1, значит 3 – 1 = 2.
Ответ: 1 сплав – 1 кг, 2 сплав – 2 кг
Слайд 323 способ. Правило «креста»
5 + 10 = 15 частей в 3 кг
3 : 15 = 0,2 кг – в 1 части.
На 5 частей – 0,2 ∙ 5 = 1 кг
На 10 частей - 0, 2∙10 = 2 кг
Ответ : 1 сплав – 1 кг,
2 сплав – 2 кг.
Слайд 3330 кг
(30-x)кг
Хкг
+
=
10%
25%
20%
10Х+(30-Х)=30*20
Ответ : 1 сплав – 1 кг,
4 способ. Метод «стаканчиков»
Слайд 391. Хр. – 100%
Ур. – (100 + t)%
в понедельник
2. 0,01Х * (100 +t)р. – 100%
Zр. - (100-t)%
Z = 0,0001Х *(10000- t2)р. – стоят акции во вторник
3. Хр. – 100%
0,0001Х *(10000- t2)р. – 96%
96 Х = 0,01Х * (10000- t2)
9600 = 10000 - t2
t = 20
Ответ : акции подорожали в понедельник на 20%
№ 99566 В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Слайд 40По данным исследований в памяти человека остаётся
¼ часть услышанного материала,
½ часть увиденного и услышанного,
¾ части материала, если ученик привлечён в активные действия в процессе обучения.