- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике (профиль) на тему Модуль. Решение уравнений с модулем
Содержание
- 1. Презентация по математике (профиль) на тему Модуль. Решение уравнений с модулем
- 2. Метод интервалов Найдём нули подмодульных выражений: х=-5,
- 3. Метод интервалов|х+2 |+|х+3|=хРаспознавание: справа от знака равно
- 4. Метод возведения в квадрат
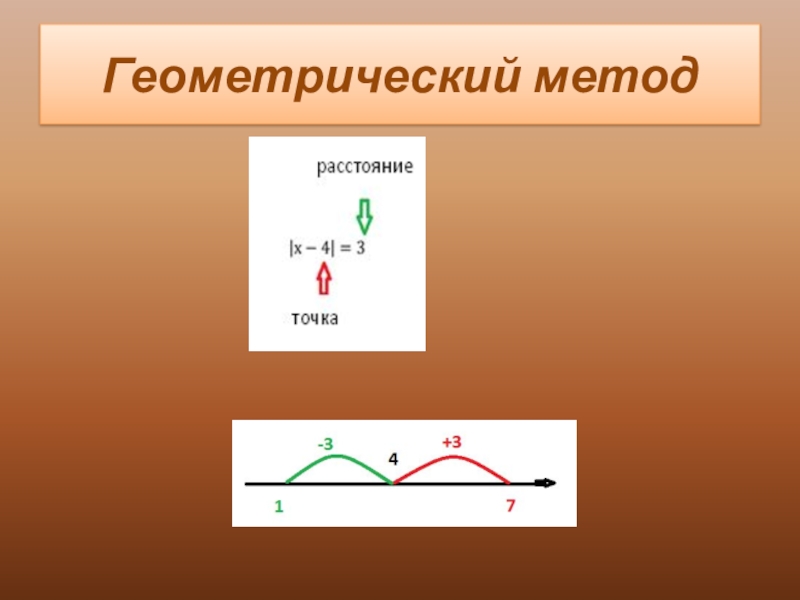
- 5. Геометрический метод
- 6. На основании ОДЗ модуля
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. На основании свойств модуляТо есть , если
- 11. Метод замены
Метод интервалов Найдём нули подмодульных выражений: х=-5, х=3Нанесём нули на координатную прямую и увидим , что она разбилась на три промежуткаНайдём знак каждого модуля на каждом из промежутков. Для этого выберем произвольно числа принадлежащие этим промежуткам
Слайд 2Метод интервалов
Найдём нули подмодульных выражений: х=-5, х=3
Нанесём нули на координатную
прямую и увидим , что она разбилась на три промежутка
Найдём знак каждого модуля на каждом из промежутков.
Для этого выберем произвольно числа принадлежащие этим промежуткам и подставим из в подмодульное выражение.
Знак полученного результата покажет нам , как будет раскрыт модуль
х<-5, пусть х=-6, тогда -6+6=-1, -6-3=-9 . оба модуля раскроются «по отрицательному типу»
-5≤х<3 пусть х=0, тогда 0+5=5, 0-3=-3. Первый модуль откроется «по отрицательному типу», второй «по положительному типу»
х≥3. Пусть х=4, тогда 4+5=9, 4-3=1. То есть оба модуля открываются «по положительному типу».
Запишем соответствующие уравнения на каждом промежутке.
Запомним ,что крайняя точка промежутка входит в промежуток , стоящий справа от неё.
Найдём знак каждого модуля на каждом из промежутков.
Для этого выберем произвольно числа принадлежащие этим промежуткам и подставим из в подмодульное выражение.
Знак полученного результата покажет нам , как будет раскрыт модуль
х<-5, пусть х=-6, тогда -6+6=-1, -6-3=-9 . оба модуля раскроются «по отрицательному типу»
-5≤х<3 пусть х=0, тогда 0+5=5, 0-3=-3. Первый модуль откроется «по отрицательному типу», второй «по положительному типу»
х≥3. Пусть х=4, тогда 4+5=9, 4-3=1. То есть оба модуля открываются «по положительному типу».
Запишем соответствующие уравнения на каждом промежутке.
Запомним ,что крайняя точка промежутка входит в промежуток , стоящий справа от неё.
Таким образом, решением данного уравнения стал промежуток х≥3.
Слайд 3Метод интервалов
|х+2 |+|х+3|=х
Распознавание: справа от знака равно переменная, а слева –
разность или сумма модулей.
Найдём нули подмодульных выражений: х=-2, х=-3. Переменная х не стоит под модулем , и её нуль находить не нужно
Для удобства решения перепишем уравнение по ходу увеличения корня. Поскольку от перемены мест слагаемых сумма не изменяется, то уравнение примет вид |х+3|+|х+2|=х
Нанесём нули на координатную прямую и увидим , что она разбилась на три промежутка
Найдём знак каждого модуля на каждом из промежутков. Для этого выберем произвольно числа принадлежащие этим промежуткам и подставим из в подмодульное выражение. Знак полученного результата покажет нам , как будет раскрыт модуль
х<-3, пусть х=-5, тогда -5+2=-3, -5-3=-8 . оба модуля раскроются «по отрицательному типу»
-3≤х<-2 пусть х=-2.5, тогда первый модуль откроется «по отрицательному типу», второй «по положительному типу»
х≥-2. Пусть х=4, тогда оба модуля открываются «по положительному типу».
Найдём нули подмодульных выражений: х=-2, х=-3. Переменная х не стоит под модулем , и её нуль находить не нужно
Для удобства решения перепишем уравнение по ходу увеличения корня. Поскольку от перемены мест слагаемых сумма не изменяется, то уравнение примет вид |х+3|+|х+2|=х
Нанесём нули на координатную прямую и увидим , что она разбилась на три промежутка
Найдём знак каждого модуля на каждом из промежутков. Для этого выберем произвольно числа принадлежащие этим промежуткам и подставим из в подмодульное выражение. Знак полученного результата покажет нам , как будет раскрыт модуль
х<-3, пусть х=-5, тогда -5+2=-3, -5-3=-8 . оба модуля раскроются «по отрицательному типу»
-3≤х<-2 пусть х=-2.5, тогда первый модуль откроется «по отрицательному типу», второй «по положительному типу»
х≥-2. Пусть х=4, тогда оба модуля открываются «по положительному типу».
Слайд 10На основании свойств модуля
То есть , если равенство выполняется, то его
можно заменить произведением.
Метод используется когда в подмодульных выражениях переменная стоит в степени