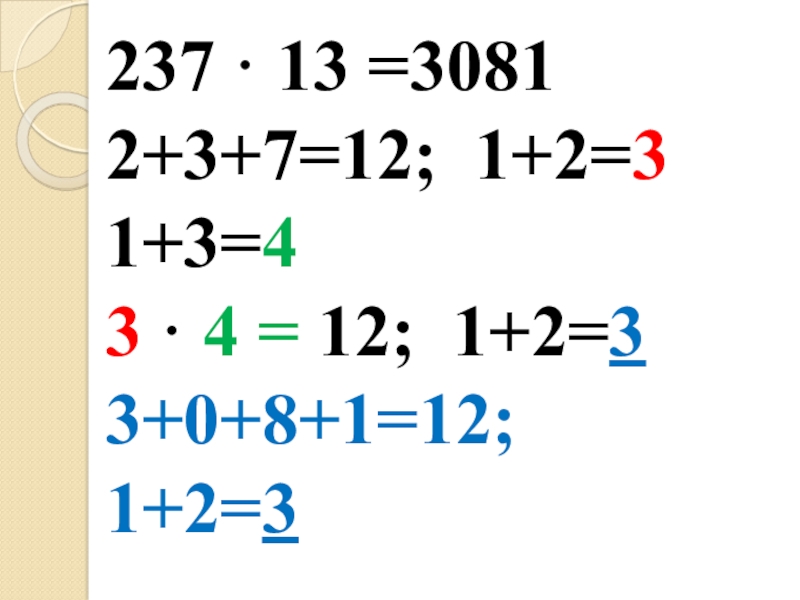- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Приёмы устного счёта
Содержание
- 1. Презентация по математике Приёмы устного счёта
- 2. Проблема: На контрольных и самостоятельных работах большая
- 3. Цель: Найти и освоить приёмы, позволяющие выполнить
- 4. Введение У́стный счёт — математические вычисления, осуществляемые человеком
- 5. Если углубиться в историю, можно заметить,что и
- 6. Феномен особых способностей в
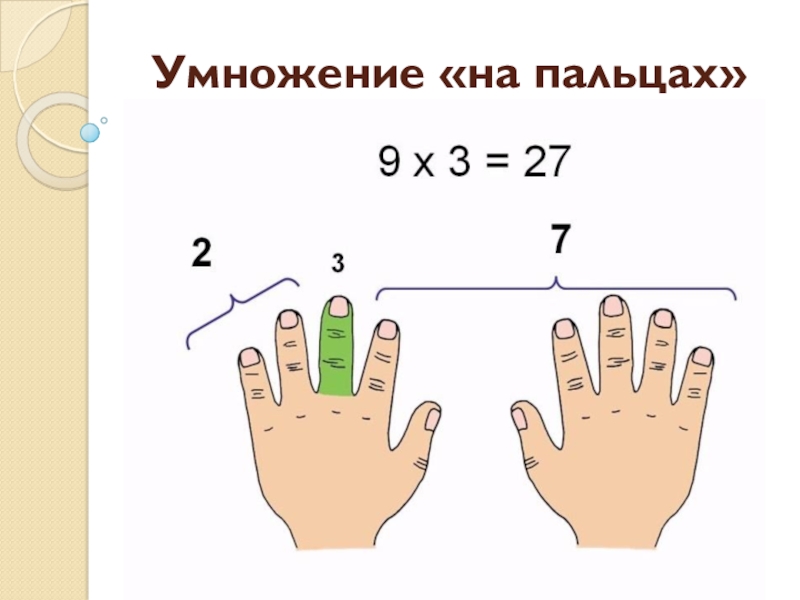
- 7. Умножение «на пальцах»
- 8. Слайд 8
- 9. Приёмы устного счёта Умножение на 11. Первую
- 10. 2 случай: сумма цифр двузначного числа больше
- 11. Умножение на 111, 1111 и т.д.Чтобы число
- 12. А если число не двузначное? Правило: Добавь
- 13. Умножение на 5. Для того что
- 14. Умножение на 4. Для того что
- 15. Умножение на 101. Чтобы умножить двузначное число
- 16. Умножение на 9. Чтобы устно умножить число
- 17. Деление на 4.Для того что бы
- 18. Деление. Часто удобно выполнять деление, увеличив или
- 19. Умножение на 1,5 Чтобы умножить число
- 20. Умножение на 15.Чтобы число умножить на
- 21. Умножение на 2,5 . Аналогично умножаем на
- 22. Умножение на 25 . Чтобы умножить
- 23. Для проверки умножения я должен найти три
- 24. 237 · 13 =30812+3+7=12; 1+2=31+3=4 3 · 4 = 12; 1+2=33+0+8+1=12; 1+2=3
- 25. Спасибо за внимание!
Проблема: На контрольных и самостоятельных работах большая часть времени уходит на вычисления, и, тем не менее, не редки вычислительные ошибки. Актуальность: Необходимость устного счёта возникает повсеместно: на уроках (и не только математики), при сдаче ОГЭ и
Слайд 1Приемы устного счета
Работу выполнили
ученики 6 «Б» класса
МАОУ СШ№145
Руководитель – Коркина Н.Г.
Слайд 2Проблема: На контрольных и самостоятельных работах большая часть времени уходит на
вычисления, и, тем не менее, не редки вычислительные ошибки.
Актуальность: Необходимость устного счёта возникает повсеместно: на уроках (и не только математики), при сдаче ОГЭ и ЕГЭ, в повседневной жизни. На уроках нас знакомили с приёмами устного счёта, но некоторые из них уже позабылись. Никакого единого справочника по приёмам устного счёта мне найти не удалось.
Актуальность: Необходимость устного счёта возникает повсеместно: на уроках (и не только математики), при сдаче ОГЭ и ЕГЭ, в повседневной жизни. На уроках нас знакомили с приёмами устного счёта, но некоторые из них уже позабылись. Никакого единого справочника по приёмам устного счёта мне найти не удалось.
Слайд 3Цель: Найти и освоить приёмы, позволяющие выполнить действия с числами устно,
быстро и безошибочно.
Задачи:
1. Выяснить, пользуются ли учащиеся нашей параллели при выполнении работ по математике приёмами устного счёта.
2. Изучить литературу по соответствующему вопросу.
3. Систематизировать изученный мной материал, выбрать наиболее интересные и часто необходимые приёмы устного счёта.
4. Обосновать принцип работы приёмов устного счёта.
5. Составить справочник-презентацию на данную тему.
6. Познакомить одноклассников с результатами своей работы.
Задачи:
1. Выяснить, пользуются ли учащиеся нашей параллели при выполнении работ по математике приёмами устного счёта.
2. Изучить литературу по соответствующему вопросу.
3. Систематизировать изученный мной материал, выбрать наиболее интересные и часто необходимые приёмы устного счёта.
4. Обосновать принцип работы приёмов устного счёта.
5. Составить справочник-презентацию на данную тему.
6. Познакомить одноклассников с результатами своей работы.
Слайд 4Введение
У́стный счёт — математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер,
калькулятор, счеты и т. п.) и часто без приспособлений ( ручка, карандаш, бумага и т. п.).
Слайд 5Если углубиться в историю, можно заметить,что и в прошлые века устный
счет был одним из главных компонентов урока. В XIX веке художник Н.П.Богданов- Бельский написал картину «Усный счет»(1895г.). На ней изображен фрагмент урока математики в школе села Татево Смоленской губернии, которую основал и в которой работал С.А.Рачинский – учитель художника, автор ряда книг по занимаельной математике: «1001 задача для устного счета», «Арифметические забавы», «Геометрические забавы».
Слайд 6 Феномен особых способностей в устном счёте встречается с
давних пор. Как известно, ими обладали многие учёные, в частности, Андре Ампер и Карл Гаусс. Однако, умение быстро считать было присуще и многим людям, чья профессия была далека от математики и науки в целом.
Хотя некоторые специалисты уверяли, что дело во врождённых способностях, другие аргументированно доказывали обратное: «дело не только и не столько в каких-то исключительных, «феноменальных» способностях, а в знании некоторых математических законов, позволяющих быстро производить вычисления» и охотно раскрывали эти законы.
Попробуем и мы познакомится хотя бы с некоторыми из этих законов.
Хотя некоторые специалисты уверяли, что дело во врождённых способностях, другие аргументированно доказывали обратное: «дело не только и не столько в каких-то исключительных, «феноменальных» способностях, а в знании некоторых математических законов, позволяющих быстро производить вычисления» и охотно раскрывали эти законы.
Попробуем и мы познакомится хотя бы с некоторыми из этих законов.
Слайд 9Приёмы устного счёта
Умножение на 11. Первую и последнюю цифры оставьте без
изменения, а между ними запишите их сумму.
Например:
17·11=1(1+7)7=187
Упражнения для закрепления: 18∙11= 23∙11=
27∙11= 52∙11=
36∙11= 61∙11=
17∙11= 43∙11=
Например:
17·11=1(1+7)7=187
Упражнения для закрепления: 18∙11= 23∙11=
27∙11= 52∙11=
36∙11= 61∙11=
17∙11= 43∙11=
Слайд 102 случай: сумма цифр двузначного числа больше или равна 10.
надо мысленно
раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю оставить без изменений.
Например:
39 · 11 = 3 (3 +9) 9 = 429
Упражнения для закрепления: 48∙11= 67∙11=
29∙11= 86∙11=
38∙11= 97∙11=
47∙11= 69 ∙11=
Например:
39 · 11 = 3 (3 +9) 9 = 429
Упражнения для закрепления: 48∙11= 67∙11=
29∙11= 86∙11=
38∙11= 97∙11=
47∙11= 69 ∙11=
Слайд 11Умножение на 111, 1111 и т.д.Чтобы число умножить на 11, 111.
и т. д., надо мысленно цифры этого числа раздвинуть на два, три и т. д. шагов, сложить цифры и записать между раздвинутыми цифрами.
Например:
24 · 111 = 2 (2+4) (2+4) 4 = 2664;
36 ·111 = 3 (3+6) (3+6) 6 = 3996;
17 · 1111 = 1 (1+7) (1+7) (1+7) 7 = 18887.
Упражнения для закрепления: 18∙111= 62∙1111=
35∙111= 21∙1111=
45∙111= 34∙1111=
32∙111= 43∙1111=
Например:
24 · 111 = 2 (2+4) (2+4) 4 = 2664;
36 ·111 = 3 (3+6) (3+6) 6 = 3996;
17 · 1111 = 1 (1+7) (1+7) (1+7) 7 = 18887.
Упражнения для закрепления: 18∙111= 62∙1111=
35∙111= 21∙1111=
45∙111= 34∙1111=
32∙111= 43∙1111=
Слайд 12А если число не двузначное?
Правило: Добавь цифру к ее соседу.
(Под соседом подразумевается цифра справа.)
Например: 1452 ·11=15972
0,3425 × 11 = 3,7675
0,3425 × 11 = (0+3), (3+4)(4+2)(2+5)(5+0) = 3,7675
Упражнения для закрепления: 324∙11= 153∙11=
256∙11= 132∙11=
1234∙11= 3523∙11=
743∙11= 433∙11=
Например: 1452 ·11=15972
0,3425 × 11 = 3,7675
0,3425 × 11 = (0+3), (3+4)(4+2)(2+5)(5+0) = 3,7675
Упражнения для закрепления: 324∙11= 153∙11=
256∙11= 132∙11=
1234∙11= 3523∙11=
743∙11= 433∙11=
Слайд 13
Умножение на 5. Для того что бы умножить число на
5 надо его умножить на 10 и поделить на 2 или сначала поделить на 2, а затем умножить на 10.
Например: 5·97=97·10:2=485
126 ·5=126:2·10=630
(умножение на 50: делить на 2 умножить на 100)
Упражнения для закрепления:37·5= 23·5=
46·5= 62·5=
74·5= 38·5=
39·5= 43·5=
Например: 5·97=97·10:2=485
126 ·5=126:2·10=630
(умножение на 50: делить на 2 умножить на 100)
Упражнения для закрепления:37·5= 23·5=
46·5= 62·5=
74·5= 38·5=
39·5= 43·5=
Слайд 14 Умножение на 4. Для того что бы умножить число на
4 его надо дважды удвоить
Например:4·20=(2·20)+(2·20)=80
Упражнения для закрепления:
36 · 4 = 48 · 4 =
84 · 4 = 2,7 · 4 =
123 · 4 = 72 · 4 =
38·4= 67 · 4=
Например:4·20=(2·20)+(2·20)=80
Упражнения для закрепления:
36 · 4 = 48 · 4 =
84 · 4 = 2,7 · 4 =
123 · 4 = 72 · 4 =
38·4= 67 · 4=
Слайд 15Умножение на 101. Чтобы умножить двузначное число на 101 надо к
этому числу приписать справа тоже число.
Например:32·101=3232
Упражнения для закрепления:48·101= 215·101=
57·101= 79·101=
63·101= 86·101=
38·101= 78·101=
Например:32·101=3232
Упражнения для закрепления:48·101= 215·101=
57·101= 79·101=
63·101= 86·101=
38·101= 78·101=
Слайд 16Умножение на 9. Чтобы устно умножить число на 9, приписывают к
нему ноль и отнимают множимое.
Например:9·15=15·10-15=150-15=135
Упражнения для закрепления: 29·9= 43·9=
47·9= 39·9=
53·9= 84·9=
69·9= 73·9=
Например:9·15=15·10-15=150-15=135
Упражнения для закрепления: 29·9= 43·9=
47·9= 39·9=
53·9= 84·9=
69·9= 73·9=
Слайд 17 Деление на 4.Для того что бы число разделить на 4
надо его дважды разделить на 2.
Например:56:4=56:2:2=6
Упражнения для закрепления:68:4= 86:4=
72:4= 96:4=
62:4= 126:4=
98:4= 148:4=
Например:56:4=56:2:2=6
Упражнения для закрепления:68:4= 86:4=
72:4= 96:4=
62:4= 126:4=
98:4= 148:4=
Слайд 18Деление. Часто удобно выполнять деление, увеличив или уменьшив и делимое и
делитель в одно и то же количество раз:
a : b = (a : c) : (b : c)
Например: 32 : 40=8 : 10=0,8
49 : 14=7 : 2=3,5
36 : 15=12 : 5=24 : 10=2,4
Упражнения для закрепления: 64:16= 54:27=
81:36= 24:16=
45:30= 48:32=
88:48= 32:24=
a : b = (a : c) : (b : c)
Например: 32 : 40=8 : 10=0,8
49 : 14=7 : 2=3,5
36 : 15=12 : 5=24 : 10=2,4
Упражнения для закрепления: 64:16= 54:27=
81:36= 24:16=
45:30= 48:32=
88:48= 32:24=
Слайд 19 Умножение на 1,5 Чтобы умножить число на 1,5, прибавьте к
числу (множимому) его половину.
Например: 28 · 1,5 = 28 + 28:2 = 28 + 14= 42
Обоснование: 28 ·1,5 = 28 ·(1 +0,5) = 28·1 + 28 ·0,5 = 28 + 28 : 2 = 28 +14 = 42
Упражнения для закрепления: 26·1,5= 44·1,5=
42·1,5= 56·1,5=
38·1,5= 82·1,5=
86·1,5= 78·1,5=
Например: 28 · 1,5 = 28 + 28:2 = 28 + 14= 42
Обоснование: 28 ·1,5 = 28 ·(1 +0,5) = 28·1 + 28 ·0,5 = 28 + 28 : 2 = 28 +14 = 42
Упражнения для закрепления: 26·1,5= 44·1,5=
42·1,5= 56·1,5=
38·1,5= 82·1,5=
86·1,5= 78·1,5=
Слайд 20 Умножение на 15.Чтобы число умножить на 15, можно его умножить
на 1,5 воспользовавшись предыдущим приёмом), а затем умножить на 10.
Например: 28 · 15 = 28 · 1,5 · 10 = (28 + 28:2) · 10 = (28 + 14) · 10 = 420
Обоснование: a · 15 = a · (1,5 · 10) = (a ·1,5) ·10
Упражнения для закрепления: 26·15= 44·15=
42·15= 56·15=
38·15= 82·15=
64·15= 88·15=
Например: 28 · 15 = 28 · 1,5 · 10 = (28 + 28:2) · 10 = (28 + 14) · 10 = 420
Обоснование: a · 15 = a · (1,5 · 10) = (a ·1,5) ·10
Упражнения для закрепления: 26·15= 44·15=
42·15= 56·15=
38·15= 82·15=
64·15= 88·15=
Слайд 21Умножение на 2,5 . Аналогично умножаем на 2,5: к удвоенному числу
прибавляем половину множимого.
Например: 38 · 2,5 = 38 · 2,5 + · 38 = 76 + 19 = =95
Упражнения для закрепления: 34∙2,5= 48∙2,5=
49∙2,5= 82∙2,5=
54∙2,5= 22∙2,5=
72·2,5= 58·2,5=
Например: 38 · 2,5 = 38 · 2,5 + · 38 = 76 + 19 = =95
Упражнения для закрепления: 34∙2,5= 48∙2,5=
49∙2,5= 82∙2,5=
54∙2,5= 22∙2,5=
72·2,5= 58·2,5=
Слайд 22 Умножение на 25 . Чтобы умножить число на 25, надо
его разделить на 4, затем умножить на 100 (аналогично, чтобы умножить число на 25, надо его разделить на 4 , а затем умножить на 1000
Например:100 · 25 =100 : 4=25·100=2500
Обоснование: a·25=a·(100:4)=(a:4) ·100
Упражнения для закрепления: 2,8·25 = 1.6·25=
48·25= 2,4·25=
36·25= 3,6·25=
62·25= 1,2·25=
Например:100 · 25 =100 : 4=25·100=2500
Обоснование: a·25=a·(100:4)=(a:4) ·100
Упражнения для закрепления: 2,8·25 = 1.6·25=
48·25= 2,4·25=
36·25= 3,6·25=
62·25= 1,2·25=
Слайд 23Для проверки умножения я должен найти три суммы цифр:
сумму цифр
первого множителя, сумму цифр второго множителя и сумму цифр произведения.
Например, я решил пример 237•42=9954 и хочу проверить результат.
Нахожу сумму цифр первого множителя, пока не получу однозначное число (237) 2+3+7=12, 1+2=3
Нахожу сумму цифр второго множителя (42) 4+2=6.
Нахожу сумму цифр произведения (9954) 9+9+5+4=18 , 1+8=9
Правило для проверки вычисления таково:
Перемножьте суммы цифр первого и второго множителя, то есть 3•6=18.
Найти сумму цифр полученного произведения. 1+8=9
Сравнить полученную сумму цифр с суммой цифр результата.
Если они не равны, значит, где-то сделана ошибка. В моем случае сумма цифр результата 1+8=9 и сумма цифр произведения 1+8=6. Это говорит о том, что пример я решил правильно.
Например, я решил пример 237•42=9954 и хочу проверить результат.
Нахожу сумму цифр первого множителя, пока не получу однозначное число (237) 2+3+7=12, 1+2=3
Нахожу сумму цифр второго множителя (42) 4+2=6.
Нахожу сумму цифр произведения (9954) 9+9+5+4=18 , 1+8=9
Правило для проверки вычисления таково:
Перемножьте суммы цифр первого и второго множителя, то есть 3•6=18.
Найти сумму цифр полученного произведения. 1+8=9
Сравнить полученную сумму цифр с суммой цифр результата.
Если они не равны, значит, где-то сделана ошибка. В моем случае сумма цифр результата 1+8=9 и сумма цифр произведения 1+8=6. Это говорит о том, что пример я решил правильно.