- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Практическое применение теоремы Пифагора
Содержание
- 1. Презентация по математике Практическое применение теоремы Пифагора
- 2. В конце девятнадцатого века высказывались разнообразные предположения
- 3. Цель исследования – выяснить области применения теоремы Пифагора.
- 4. Предмет исследования: применение Теоремы Пифагора при решении практических задач.
- 5. Гипотеза исследования - с помощью теоремы Пифагора можно решать не только математические задачи.
- 6. Задачи исследования :Собрать информацию о практическом применении
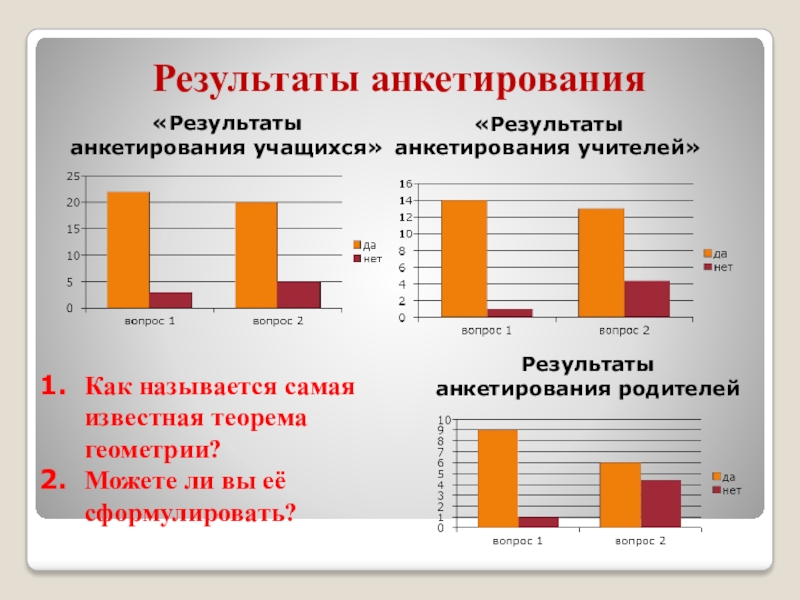
- 7. Результаты анкетирования«Результаты анкетирования учащихся»«Результаты анкетирования учителей»Результаты анкетирования
- 8. Пифагор – самая загадочная личность, человек-символ, философ,
- 9. Пифагор Самосский (ок. 580 - ок.
- 10. История теоремыИсторический обзор начнем с древнего Китая.
- 11. Кантор (крупнейший немецкий историк математики) считает, что
- 12. Несколько больше известно о теореме Пифагора у
- 13. Теорема Пифагора в древних практических задачах Над
- 14. Из учебника"Арифметика" на Руси. Случися некоему
- 15. Задача индийского математика XII века Бхаскары На
- 16. СтроительствоОкноВ зданиях готического и ромaнского стиля верхние
- 17. Слайд 17
- 18. В доме задумано построить двускатную крышу (форма
- 19. Установка вертикальной мачты ВС =Задача 1. Вертикальная
- 20. МолниеотводМолниеотвод защищает от молнии все предметы, расстояние
- 21. Модель молниеотвода для крыши моей времянкиВ нашей
- 22. Я измерил высоту и ширину крыши. Известно,
- 23. Астрономия 12 апреля 1961
- 24. Путь светового лучаНа этом рисунке показаны точки
- 25. На этом
- 26. Треугольник ABC
- 27. В армии Задача. Параллельно стенду на расстоянии
- 28. Задача 1. Вычислите высоту слоя воды над
- 29. В сельском хозяйствеЗадача. В дождевальной установке дождеватели
- 30. В стереометрии
- 31. Слайд 31
- 32. Считать эти приложения
- 33. Работы по озеленению школы
- 34. АВС Осенью мы возле
- 35. Заключение Теорема Пифагора
- 36. Очень интересна и биография
- 37. Память
Слайд 1Практическое применение теоремы Пифагора
Работа ученика 9 класса
МОУ «Горская сош»
Мотченко Руслана
Руководитель: Токорева
Слайд 2В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса
Слайд 5Гипотеза исследования - с помощью теоремы Пифагора можно решать не только
Слайд 6Задачи исследования :
Собрать информацию о практическом применении теоремы Пифагора в различных
Изучить некоторые исторические сведения о Пифагоре и о его теореме.
Показать применение теоремы при решении исторических задач.
Решить прикладные задачи по укреплению елок и туй на школьной территории и молниеотвода.
Слайд 7Результаты анкетирования
«Результаты анкетирования учащихся»
«Результаты анкетирования учителей»
Результаты анкетирования родителей
Как называется самая известная
Можете ли вы её сформулировать?
Слайд 8Пифагор – самая загадочная личность, человек-символ, философ, пророк
Пифагор – едва ли
Слайд 9 Пифагор Самосский (ок. 580 - ок. 500 до н. э.)
Слайд 10История теоремы
Исторический обзор начнем с древнего Китая. Здесь особое внимание привлекает
"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Слайд 11Кантор (крупнейший немецкий историк математики) считает, что равенство 32 + 42
э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого . Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра.
Слайд 12Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте,
Ван-дер-Варден (голландский математик) сделал следующий вывод: "Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку."
Геометрия у индусов, как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.
Слайд 13Теорема Пифагора в древних практических задачах
Над озером тихим,
С
Он рос одиноко. И ветер порывом
Отнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока.( 3 3/4 фута)
Слайд 14 Из учебника"Арифметика" на Руси.
Случися некоему человеку к стене
Слайд 15Задача индийского математика XII века Бхаскары
На берегу реки рос
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота? (3+5 футов)
Слайд 16Строительство
Окно
В зданиях готического и ромaнского стиля верхние части окон расчленяются каменными
Слайд 18В доме задумано построить двускатную крышу (форма в сечении). Какой длины
А) Из треугольника DBC: DB=2,5м
Б) Из треугольника ABF:
Крыша
Слайд 19Установка вертикальной мачты
ВС =
Задача 1. Вертикальная мачта поддерживается четырьмя канатами,
каната потребовалось для укрепления мачты, если на узлы пошло 10 м?
Решение: По теореме Пифагора из
ВАС :
=20 м.
Учитывая, что всего 4 каната и на узлы пошло 10 м, всего потребуется 90 м каната.
Слайд 20Молниеотвод
Молниеотвод защищает от молнии все предметы, расстояние до которых от его
Решение: По теореме Пифагора h2 ≥ a2+b2, значит,
h≥ Ответ: h ≥
Слайд 21Модель молниеотвода для крыши моей времянки
В нашей местности летом часто бывают
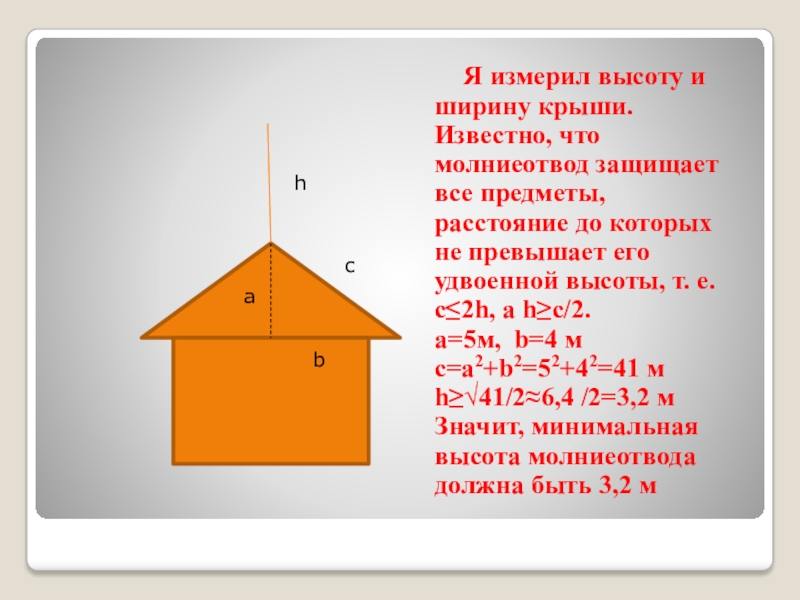
Слайд 22Я измерил высоту и ширину крыши. Известно, что молниеотвод защищает все
а=5м, b=4 м
с=a2+b2=52+42=41 м
h≥√41/2≈6,4 /2=3,2 м
Значит, минимальная высота молниеотвода должна быть 3,2 м
h
c
a
b
Слайд 23Астрономия
12 апреля 1961 года советский гражданин Ю.
расстоянии от корабля находились в это время наиболее удаленные от него и видимые космонавтом участки поверхности Земли? (Радиус Земли считать равным 6400 км.)
Слайд 24Путь светового луча
На этом рисунке показаны точки A и B и
Какой путь проходит луч? Поскольку свет идет туда и обратно одинаковый путь, спросим сразу: чему равна половина пути, который проходит луч? Если обозначить отрезок AB символом l, половину времени как t, а также обозначив скорость движения света буквой c, то наше уравнение примет вид
c * t = l
Слайд 25 На этом рисунке показан путь светового
Теперь рассмотрим треугольник ABC. Это равнобедренный треугольник, высота которого равна l. Да-да, тому самому l, которое мы ввели при рассмотрении процесса с неподвижной точки зрения. Поскольку движение происходит перпендикулярно l, то оно не могло повлиять не нее.
Слайд 26 Треугольник ABC составлен из двух половинок
s2 = l2 + d2
Это ведь просто теорема Пифагора, верно?
Слайд 27В армии
Задача. Параллельно стенду на расстоянии 500 м от него
Решение: Пусть АВ – расстояние между крайними стрелками, т.е. АВ=120 м, АК=ВЕ=500 м, AD=BC=2800 м. Из треугольника AKD по теореме Пифагора следует, что DK =
2755 м, откуда DC=2DK+AB=
5630 м.
Слайд 28Задача 1. Вычислите высоту слоя воды над линией, соединяющей две противоположные
Решение: Из
Тогда DC=0,159
В географии
Слайд 29В сельском хозяйстве
Задача. В дождевальной установке дождеватели расположены по так называемой
При каком максимальном расстоянии d между дождевателями установка будет орошать все поле, если один дождеватель орошает круг радиуса r?
Решение: На рисунке расстояние слишком велико. Расположим дождеватели так, как показано на следующем рисунке. Это наилучший вариант , поскольку при малейшем удалении дождевателей друг от друга образуются неорошаемые участки, т.е. 2d2=(2r2), откуда d=r
.