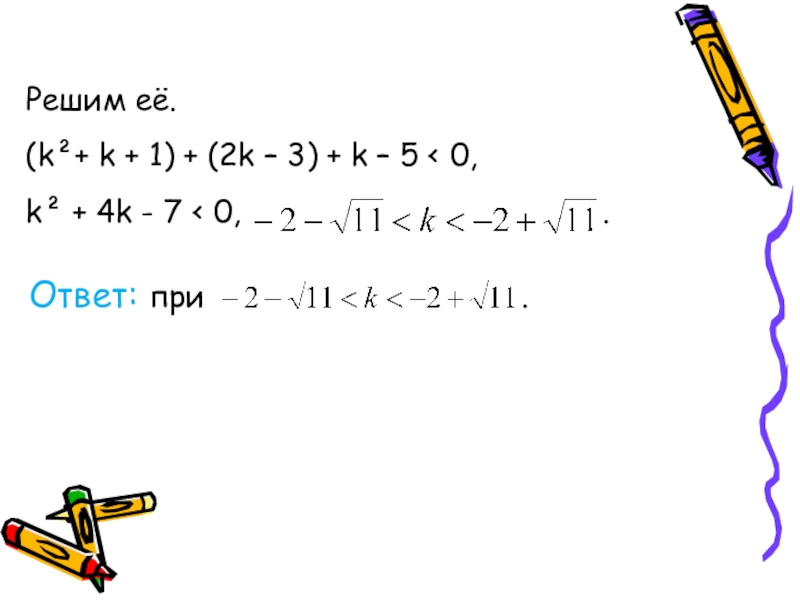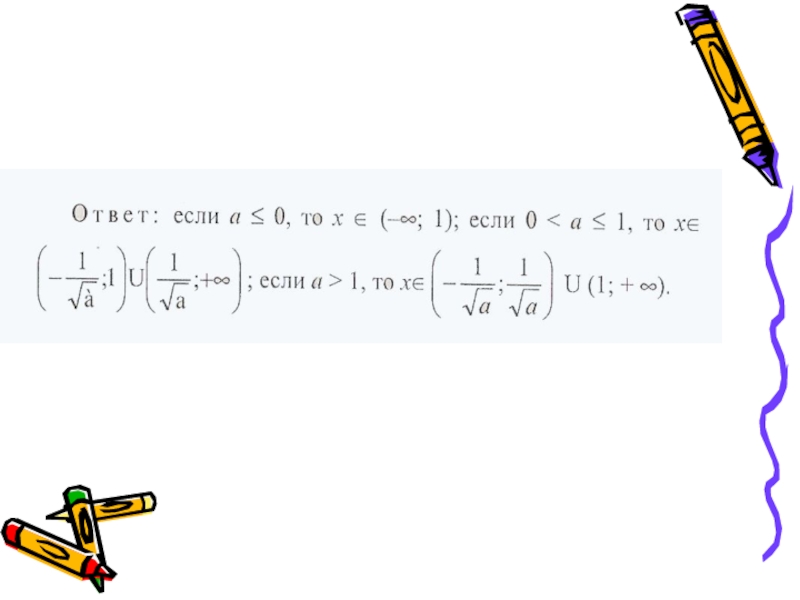- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике по теме:Подготовка 9-х классов к ОГЭ по математике по темеЗадания с параметром
Содержание
- 1. Презентация по математике по теме:Подготовка 9-х классов к ОГЭ по математике по темеЗадания с параметром
- 2. Что за прелесть эти задачи с параметрами!
- 3. Решить уравнение с параметром
- 4. Контрольные значения параметра-
- 5. Типы задач
- 6. Тип 1. Уравнения, неравенства, их системы
- 7. Способы решения задач с
- 8. Пример 1. В уравнении (α –
- 9. Пример 2. При каких значениях m
- 10. Пример 3. При каких значениях
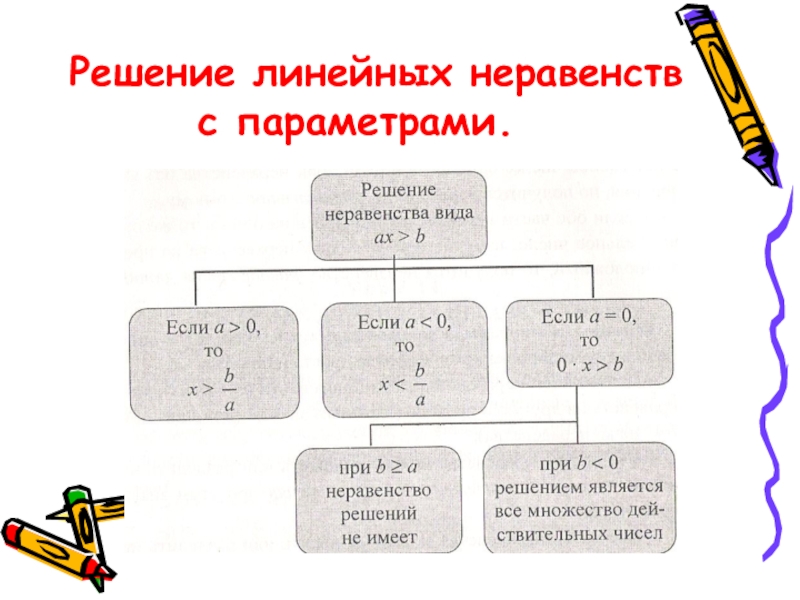
- 11. Решение линейных уравнений
- 12. При решении
- 13. Пример 1. Решить уравнение
- 14. ; 1)
- 15. Пример 2. Решить уравнение
- 16. При α = 1, заданное уравнение принимает
- 17. Задания для закрепление рассмотренного выше материала.
- 18. Ответы: 1)
- 19. . 5) при α = 0,
- 20. Решение линейных уравнений с параметрами при наличии дополнительных условий (ограничений) к корням уравнений
- 21. . Пример 1. Найти значение параметра α,
- 22. Решение линейных
- 23. Пример 1. Решить относительно x
- 24. Далее по схеме имеем: при m
- 25. Пример 2.
- 26. ..Значит, надо рассмотреть пять случаев: 1)
- 27. 4) При 0 < а < 2,
- 28. РАСПОЛОЖЕНИЕ КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ В ЗАВИСИМОСТИ ОТ ПАРАМЕТРА.
- 29. Расположение корней
- 30. Теорема 2. Для того чтобы один
- 31. Теорема 3. Для
- 32. Следствие 1.
- 33. Следствие 2. Для
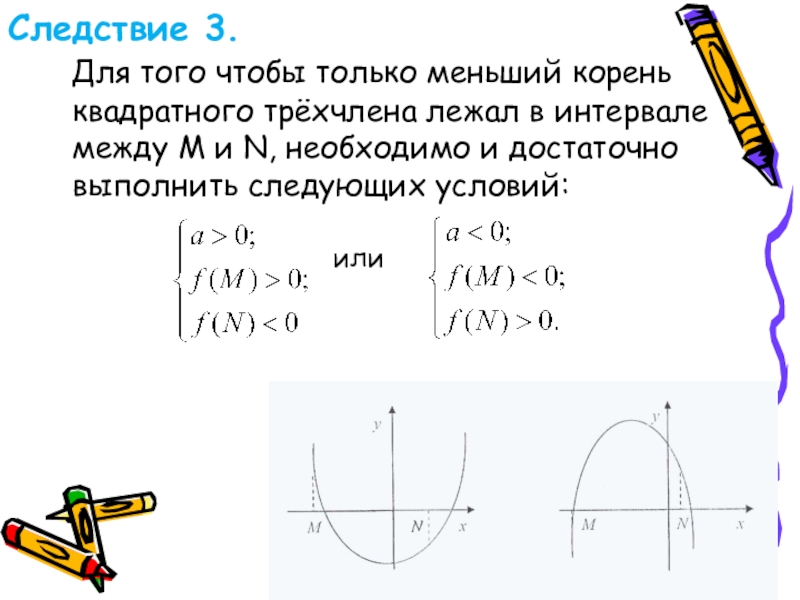
- 34. Следствие 3. Для того чтобы
- 35. Следствие 4.
- 36. Контрoльные значения параметра:
- 37. Пример 1. Найдите все значения
- 38. График функции ƒ(х)
- 39. Решим её: то есть c > 1.
- 40. Пример 2. При каких действительных значениях k
- 41. Первым двум им соответствует система: Двум другим:
- 42. Получим совокупность следующих систему:Решением которых является
- 43. Примечание.
- 44. Пример 3. При каких α корни уравнения
- 45. Заметим, что знак коэффициента α совпадает со
- 46. Пример4. При каких
- 47. Решим её. (k²+ k + 1)
- 48. Пример 5. Решить неравенство
- 49. Если D < 0,
- 50. Решение неравенств методом интервалов
- 51. Слайд 51
- 52. Слайд 52
- 53. Слайд 53
- 54. Слайд 54
- 55. Слайд 55
- 56. Слайд 56
- 57. Слайд 57
- 58. Слайд 58
- 59. Слайд 59
Слайд 2Что за прелесть эти задачи с параметрами! Каждая из них -
Слайд 3
Решить уравнение с параметром
ƒ(
уравнений, получающихся из
уравнения ƒ( x; α) = 0 при любых
действительных значениях
параметра.
Слайд 4 Контрольные значения параметра-
это те значения параметра,
которых или при переходе через
которые происходит качественное
изменения уравнения.
Слайд 6 Тип 1. Уравнения, неравенства, их системы и совокупности,
параметра (параметров), либо для значения параметра,
принадлежащих заранее оговоренному множеству.
Тип 2. Уравнения, неравенства, их системы и совокупности, для
которых требуется определить количество решений в зависимости
от значения параметра (параметров).
Тип 3. Уравнения, неравенства, их системы и совокупности, для
которых требуется найти все те значения параметра, при которых
указанные уравнения, неравенства, их системы и совокупности
имеют заданное число решений ( в частности, не имеют или имеют
бесконечное множества решений ).
Тип 4. Уравнения, неравенства, их системы и совокупности, для
которых при искомых значениях параметра множество решений
удовлетворяет заданным условиям в области
определения.
Слайд 7Способы решения задач с параметром:
Способ 1: аналитический.
Способ 3: решение
относительно параметра.
Слайд 8 Пример 1. В уравнении (α – 1) x = α
определить α так, чтобы число 3
было его корнем.
Решение.
Если число 3 является корнем уравнения,
то оно обращает его в верное равенство.
Подставим x = 3 в уравнение и решим его
относительно α: (α – 1) · 3 = α – 2;
3α – α = 3 – 2;
α = 0,5.
Итак, при α = 0,5 число 3 является корнем
уравнения (α – 1)x = α – 2.
Ответ: при α = 0,5.
Слайд 9 Пример 2. При каких значениях m
x² - 2x + 2m – 3 = 0 равен нулю.
Решение. Если x = 0, то имеем:
0² - 2·0 + 2m – 3 = 0;
2m = 3;
m = 1,5.
Поверим, не равняется ли второй корень
уравнения нулю x²- 2x = 0,
х = 0 ν х = 2.
Ответ: при m = 1,5.
Слайд 10
Пример 3.
При каких значениях параметра α
αx = 12 и 3x = α имеют общие корни?
Решение.Решим каждое уравнение при α ≠ 0
(если а =0, то первое уравнение не имеет
решения, что противоречит условию).
αx = 12, x = 12/а;
3x = α, x = а/3. Приравниваем полученные
корни 12/a = a/3, α² = 36, и получаем,
что а = 6,а = - 6.
Ответ: при a = 6, a = - 6.
.
Слайд 12 При решении линейных уравнений с
уравнения происходит при переходе
коэффициента а через нуль. То есть
контрольными значениями будут те значения
коэффициента при переменной x, при
которых он обращается в нуль, так как при
таких значениях невозможно деление на
коэффициент при x.
Слайд 13 Пример 1. Решить уравнение
Решение. Это уравнение является линейным
относительно переменой x. Контрольными будут
те значения параметра, при которых
коэффициент при x обращается в 0.
Рассмотрим случаи:
α (α – 2) = 0 и α (α – 2) ≠ 0.
Слайд 14
;
1) При α =
2)При α = 2 уравнение принимает вид: 0·x = 0,
этому уравнению удовлетворяют любые значения
переменной x. Если же параметр выбирается
не равным 0 и 2, то коэффициент при x отличен от
нуля и, следовательно, на этот коэффициент можно
разделить обе части уравнения.
Получим: x = , x = .
Ответ : при а = 0, нет корней;
при a = 2, x – любое;
при a ≠ 0, α ≠ 2, x = .
Слайд 15 Пример 2. Решить уравнение
Решение. Это уравнение является линейным
относительно переменной x. Контрольными
будут те значения параметра, при которых
коэффициент при x обращается в 0.
Рассмотрим случаи α² - 1 = 0 и α²- 1 ≠ 0.
Удобно разложить обе части уравнения на
множители: (α – 1)(α + 1)x = (α – 1)(α – 2).
Слайд 16При α = 1, заданное уравнение принимает
При α = -1, заданное уравнение принимает вид:
0 · x = 2, значит уравнение корней не имеет.
При α ≠ ± 1, можно разделить обе части уравнения
на α² - 1 ≠ 0: x = ; x = .
Ответ: при α = 1, x – любое;
при α = -1, нет корней;
при α ≠ ±1, x = .
.
Слайд 17 Задания для закрепление
рассмотренного выше материала.
Решить уравнения:
2) (α - 3) x = 6; 6) αx = α² - α;
3) (α - 3) x = α - 6; 7) (α² - 5α) x = α²-25;
4) αx = α; 8) αx - 4 = x;
9) (α²- 25)x = α² - 7α + 10.
Слайд 18
Ответы:
1) при α = 0,
при α ≠ 0, x = .
2) при α = 3, нет решения;
при α ≠ 3, x = .
3) при α = 3, нет решения;
при α ≠ 3, x = .
4) при α = 0, х – любое;
при α ≠ 0, x = 1.
Слайд 19.
5) при α = 0, х – любое; при
при.α ≠ 0 и α ≠ 1, x = .
6) при α = 0, x - любое; при α ≠ 0, x = α -1 .
7) при α = 0, нет решений;
при α = 5, x – любое ,при .α ≠ 0 α ≠ 5, х=
8) при α = 1, нет решений;
при α ≠ 1, x = .
9) при α = 5, х - любое;
при α = -5, нет решений;
при α ≠ ±5, х = .
Слайд 20Решение линейных уравнений с параметрами при наличии дополнительных условий (ограничений)
Слайд 21.
Пример 1. Найти значение параметра α,
при
имеет единственный отрицательный корень.
Решение. Данное уравнение равносильно следующему:
α(α + 3)х = (3 – α)α. Если α(α + 3) ≠ 0, то есть α ≠ 0, α ≠ -3,
то уравнение имеет единственный корень х = ,
х < 0, если < 0. Решив это неравенство методом
интервалов, имеет: α < -3 или α > 3.
Итак, данное уравнение имеет единственное
отрицательное решение при α < -3 или α > 3.
Ответ: при α < -3 или α > 3.
Слайд 23Пример 1. Решить относительно x
Решение. Данное неравенство равносильно
следующему: mx – 2х > -2 – 1 ;
(m – 2)x > -3.
Данное неравенство является линейным,
поэтому контрольным значением для него
будет m -2 = 0.
Слайд 24
Далее по схеме имеем:
при m - 2 >
при m – 2 < 0, то есть m < 2, х < ;
при m = 2 неравенство принимает вид 0 · x > - 3,
здесь x - любое действительное число.
Ответ: при m > 2, х > ;
при m < 2, x < ;
при m = 2, х - любое действительное
число.
Слайд 25 Пример 2.
Решить
Решение. Данное неравенства является линейным относительно переменной x.
Контрольными будут те значения параметра,
при которых коэффициент α(α – 2) при х обращается в 0. Нули коэффициента α = 0, α = 2 разбивают множества действительных чисел на
три промежутка: (- ∞;0) U (0;2) U (2;+∞).
Слайд 26.
.
Значит, надо рассмотреть пять случаев:
1) а = 0; 2)
1) При α = 0, неравенство принимает вид
0 · х > -2, т. е. х-любое действительное число.
2) При α = 2, неравенство принимает вид
0 · х > 0, т. е. не имеет решений.
3) При α < 0, коэффициент α(α – 2) > 0
(определим методом интервалов знаки
многочлена p(α) = α (α - 2)),
Поэтому x > , x > .
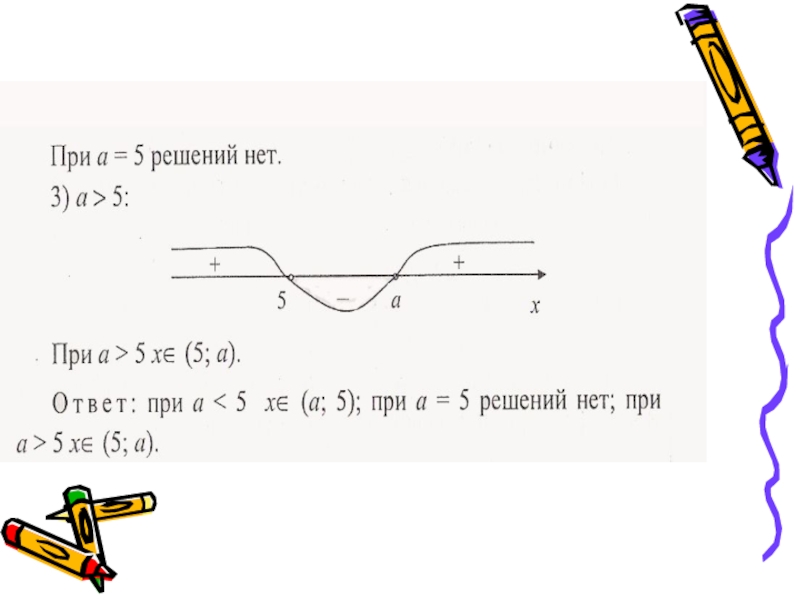
Слайд 274) При 0 < а < 2, коэффициент
5) При α > 2, коэффициент α (α – 2 ) > 0,
значит, x > .
Ответ: при α = 0, x – любое;
при α = 2, решение нет;
при 0 < α < 2, х < ;
при α < 0 или α > 2: х > .
Слайд 29
Расположение корней квадратного
уравнения в зависимости
Теорема 1. Для того чтобы оба корня
квадратного трёхчлена были меньше, чем
число М, (то есть лежали на числовой оси
левее, чем точка М), необходимо и достаточно
выполнение следующих условий:
или
Слайд 30Теорема 2.
Для того чтобы один из корней квадратного
трёхчлена был меньше, чем число М,
а другой больше, чем М (то есть точка М
лежала бы между корнями), необходимо и
достаточно выполнить следующих условий:
или
Эти две системы можно заменить формулой
а ·ƒ(М) < 0.
Слайд 31Теорема 3.
Для того чтобы оба корня
трёхчлена были больше, чем число М
(т. е. лежали на числовой оси правее, чем
точка М), необходимо и достаточно
выполнить следующие условия:
или
Слайд 32 Следствие 1.
Для того чтобы оба
трёхчлена были меньше, чем число М, но
больше числа N, то есть лежали в
интервале между М и N, необходимо и
достаточно выполнить следующих
условий:
или
Слайд 33 Следствие 2.
Для того чтобы больший
квадратного трёхчлена лежал в интервале
между М и N, необходимо и достаточно
выполнение следующих условий:
или
При этом меньший корень лежит в отрезке MN.
Слайд 34Следствие 3.
Для того чтобы только меньший корень
между М и N, необходимо и достаточно
выполнить следующих условий:
или
Слайд 35 Следствие 4.
Для того чтобы один
квадратного трёхчлена был меньше, чем
число М, а другое больше, чем N, то есть
отрезок MN лежал внутри интервала между
корнями, необходимо и достаточно
выполнение следующих условий:
или
Слайд 36
Контрoльные значения параметра:
направление ветвей параболы, знаки
значений ƒ(М), ƒ(N), расположение
вершины параболы (а все остальное
записывается по графической
иллюстрации).
Слайд 37
Пример 1. Найдите все значения
квадратного уравнения
x² + 4cx + (1 – 2с + 4с²) = 0 различны
и меньше, чем -1.
Решение.
Нашему заданию соответствует следующая
графическая иллюстрация.
Слайд 38
График функции ƒ(х) = х²+4сх +
представляет собой параболу, ветви которой
направлены вверх.
По условию эта парабола должна пересекать ось
х, причём отрезок [ х1 ; х2] должен быть левее -1.
Следовательно, значение функции при х = -1
должно быть положительным, а вершина – быть
расположена левее -1. Итак, получаем систему:
Слайд 39
Решим её:
то есть c > 1.
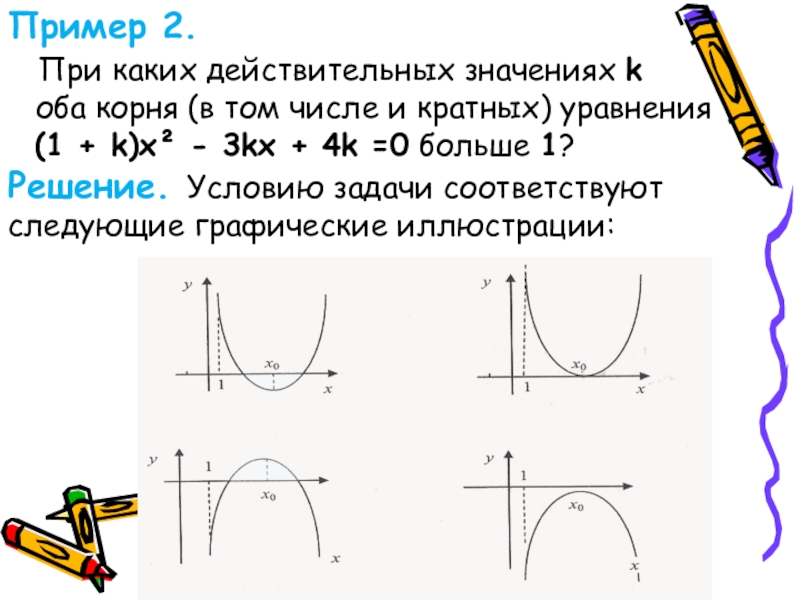
Пример 2. При каких действительных значениях k оба корня (в том числе и кратных) уравнения (1 + k)х² - 3kx + 4k =0 больше 1?
Решение. Условию задачи соответствуют следующие графические иллюстрации:
Слайд 40Пример 2.
При каких действительных значениях k
оба корня
(1 + k)х² - 3kx + 4k =0 больше 1?
Решение. Условию задачи соответствуют следующие графические иллюстрации:
Слайд 43
Примечание.
Полученная
равносильна системе
что облегчает решение задачи.
В следующем примере воспользуемся этой системой.
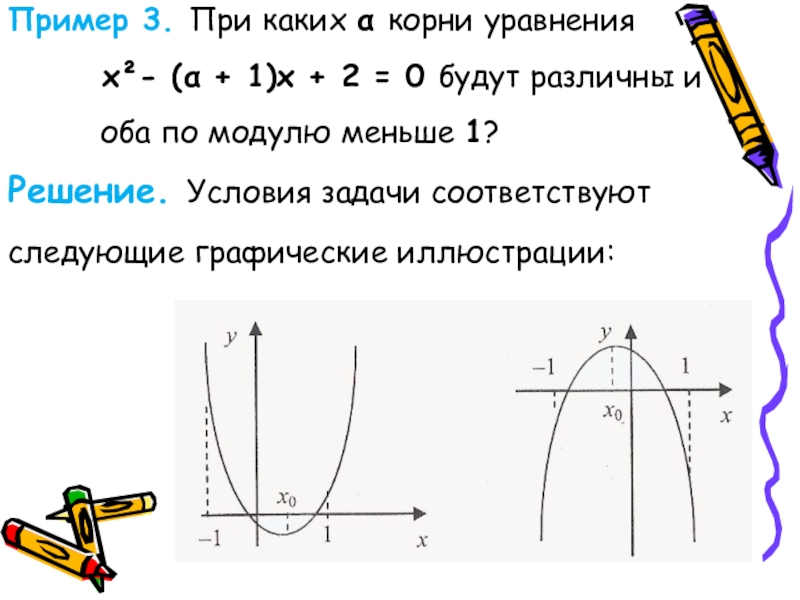
Слайд 44Пример 3. При каких α корни уравнения
оба по модулю меньше 1?
Решение. Условия задачи соответствуют следующие графические иллюстрации:
Слайд 45
Заметим, что знак коэффициента α совпадает со знаком ƒ(1), ƒ(-1), а
Решим её:
Отсюда, α > 3 + 2
Ответ : α > 3 + 2
Слайд 46 Пример4.
При каких значениях k один из
уравнения (k² + k +1)x² + (2k - 3)x + k -5=0
больше 1, а другой меньше 1?
Решение.
Так как k² + k + 1 > 0 при любых k, то по условию задачи предстает следующая
графическая иллюстрация,
которая соответствует
неравенству ƒ(1) < 0:
Слайд 48
Пример 5. Решить неравенство
Решение.
Так как старший коэффициент перед x
не равен нулю, то данное неравенство
при любых значениях α является
квадратным.
Найдём корни трёхчлена ƒ(х) = х² +αх +1.
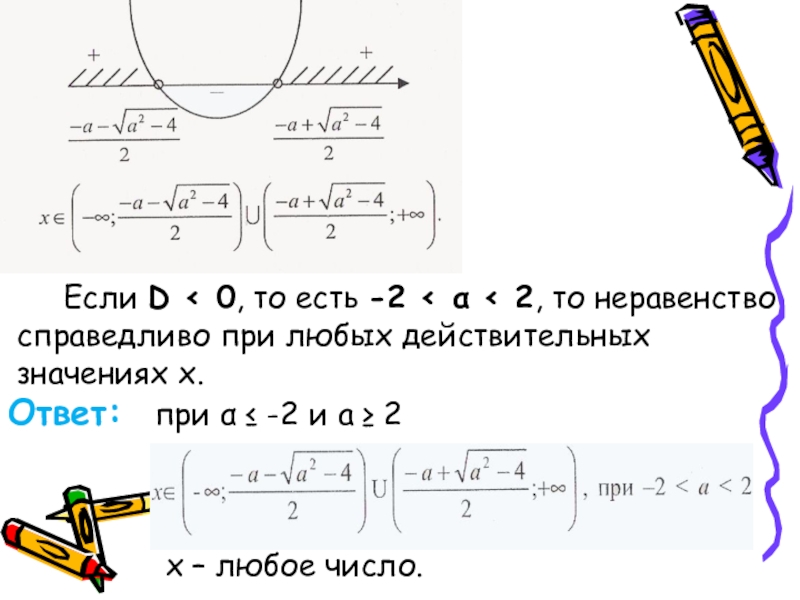
D=α²-4. Если D ≥ 0, то α ≤ -2 и а ≥ 2, то
решением неравенства будет:
Слайд 49 Если D < 0, то есть -2
справедливо при любых действительных
значениях х.
Ответ: при α ≤ -2 и а ≥ 2
х – любое число.