Научный руководитель:
Егорова Нурия Талгатовна,
учитель математики МАОУ №58 г. Уфа
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике по теме Задача Наполеона
Содержание
- 1. Презентация по математике по теме Задача Наполеона
- 2. Наполеоне Буонапарте (1769—1821)
- 3. Цель работы:Изучить задачи Наполеона и найти способ
- 4. Задачи:1) Изучить соответствующую историческую и математическую литературу.
- 5. В своей работе мы выдвинули следующее предположение:
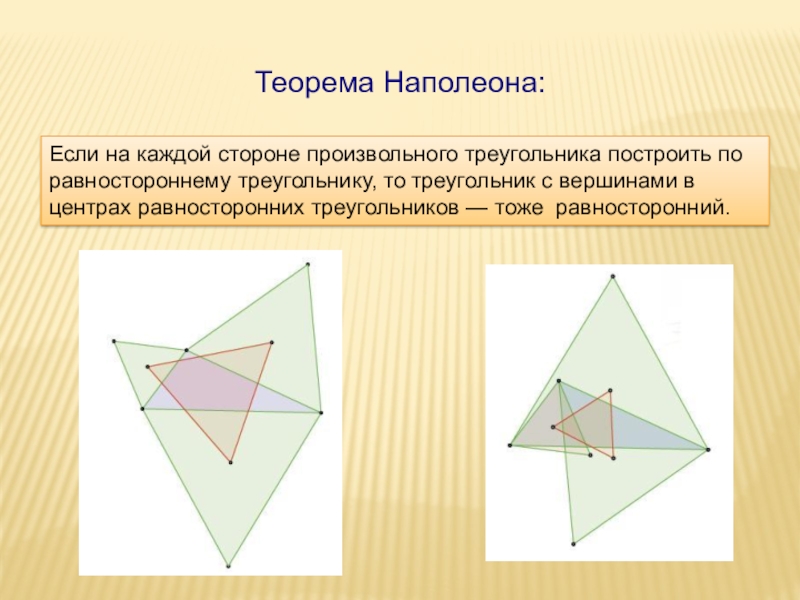
- 6. Если на каждой стороне произвольного треугольника построить
- 7. На сторонах треугольника построим во внешнюю его сторону равносторонние треугольники.Вот как это выглядит в движении.
- 8. Центры равносторонних треугольников.Вот как это выглядит в движении.
- 9. Центры равносторонних треугольников равноудалены друг от друга.Зеленый треугольник всегда равносторонний.
- 10. Слайд 10
- 11. ∠AO1С = ∠BO2А = ∠СО3В = 120°
- 12. Выделим шестиугольник АO2ВO3СO1 ,а внешние к нему
- 13. Доказательство теоремы:Следовательно, треугольник O1O2O3 равносторонний, что и требовалось
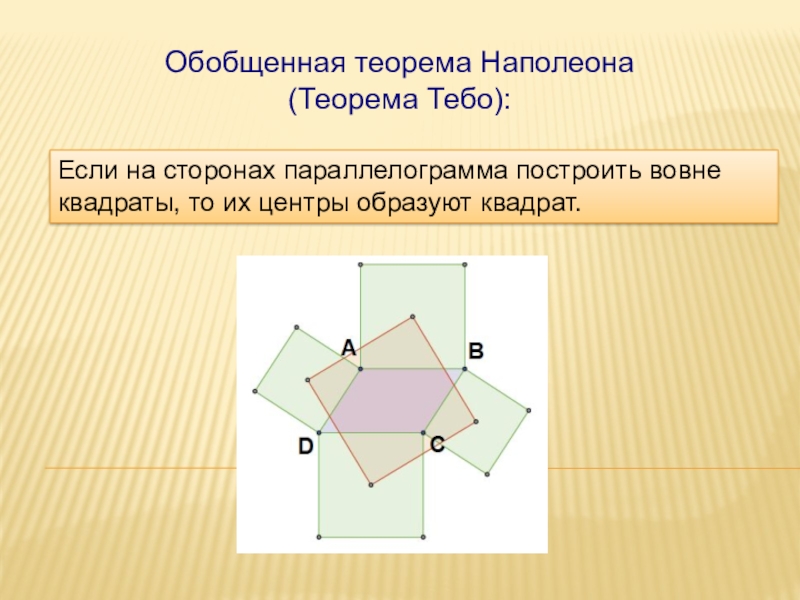
- 14. Если на сторонах параллелограмма построить вовне квадраты, то их центры образуют квадрат. Обобщенная теорема Наполеона(Теорема Тебо):
- 15. Флаг ИзраиляСледствие теоремы Наполеона:Звезда Давида — эмблема
- 16. Одно из 7 чудес света - египетские
- 17. Ответ: 2 метра 66 сантиметровДано:h 1 =
- 18. Одно из 7 чудес света - египетские
- 19. Ответ: 5 метра 32 сантиметраДано:h 1 =
- 20. Одно из 7 чудес света - египетские
- 21. Ответ: 57 метра 33 сантиметраДано:h 1 =
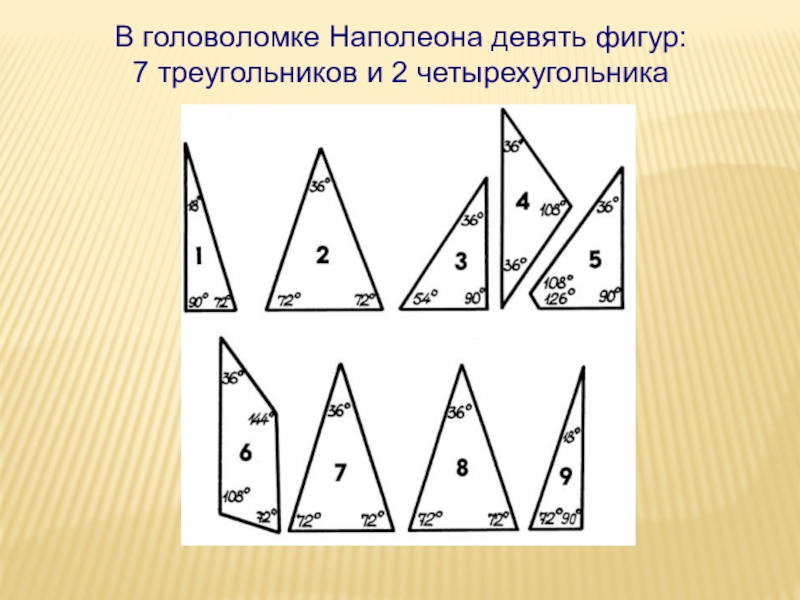
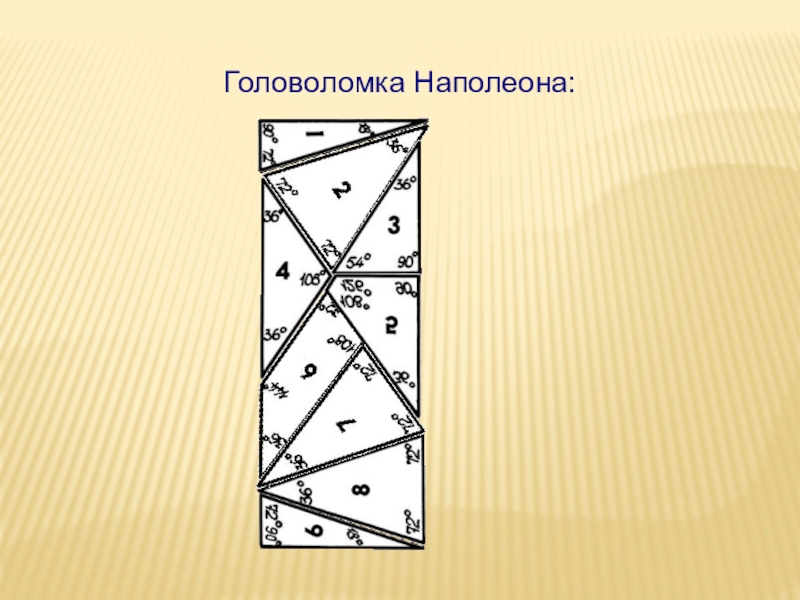
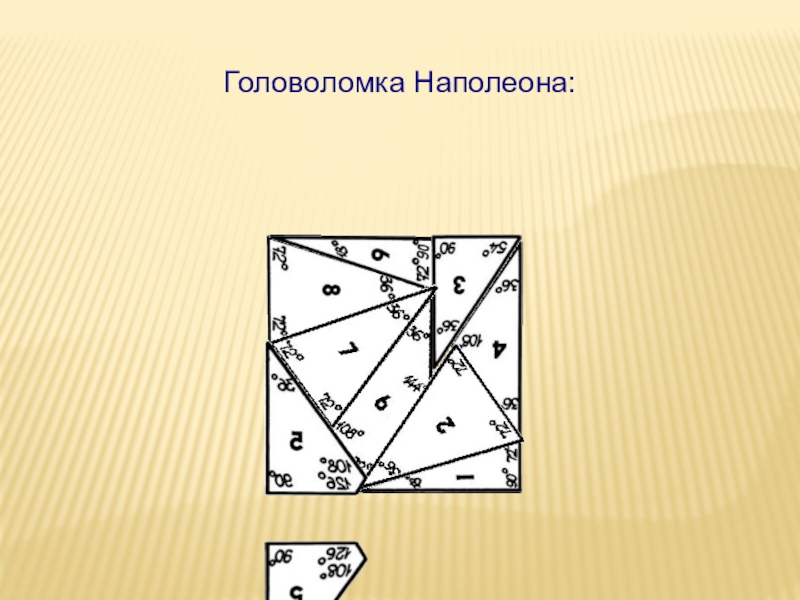
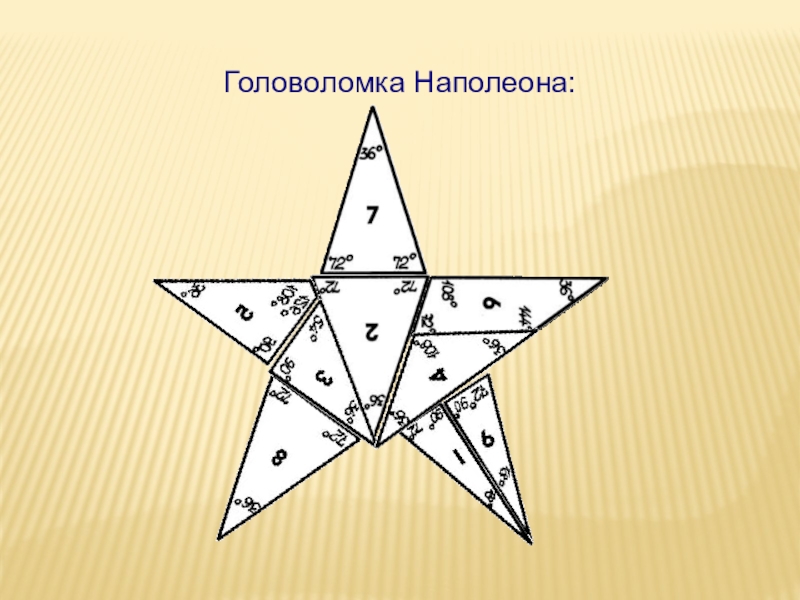
- 22. В головоломке Наполеона девять фигур:7 треугольников и 2 четырехугольника
- 23. Головоломка Наполеона:
- 24. Головоломка Наполеона:
- 25. Головоломка Наполеона:
- 26. По преданию Наполеон Бонапарт предложил итальянскому математику
- 27. По преданию Наполеон Бонапарт предложил итальянскому математику
- 28. По преданию Наполеон Бонапарт предложил итальянскому математику
- 29. Данную окружность разделить на четыре равные части, не прибегая к линейке. Положение центра окружности дано.Задача Наполеона:
- 30. 1) Анализ задачи.Разделить окружность на четыре части
- 31. 2) Построение.
- 32. 2) Построение.
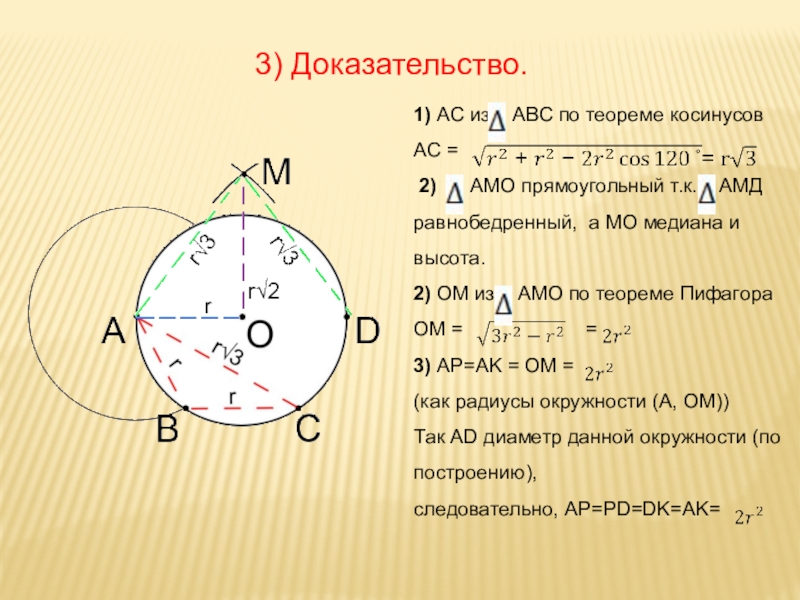
- 33. 1) АС из АВС по теореме
- 34. Так как окружность с центром в данной
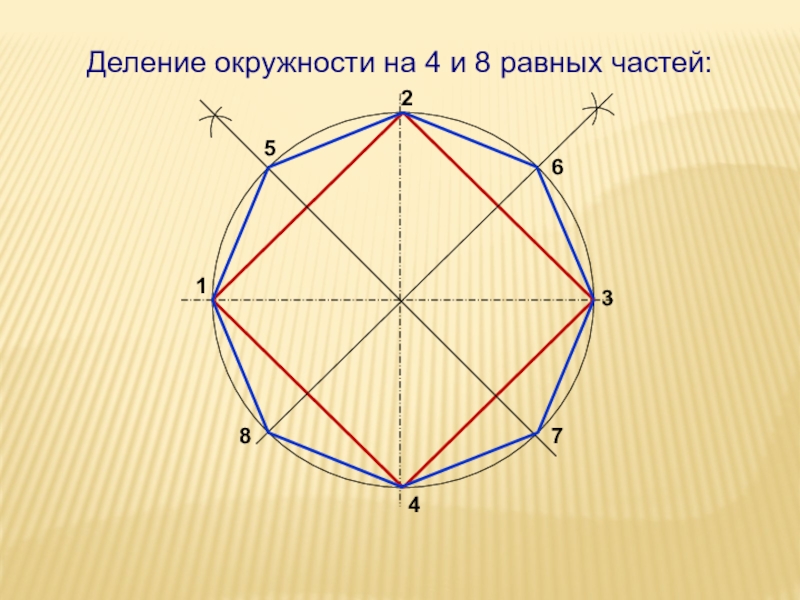
- 35. 12345678Деление окружности на 4 и 8 равных частей:
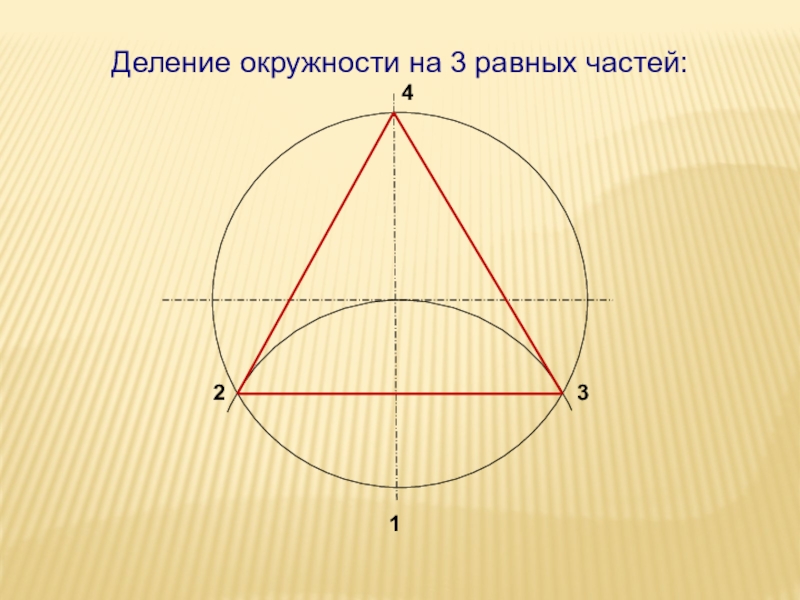
- 36. 1234Деление окружности на 3 равных частей:
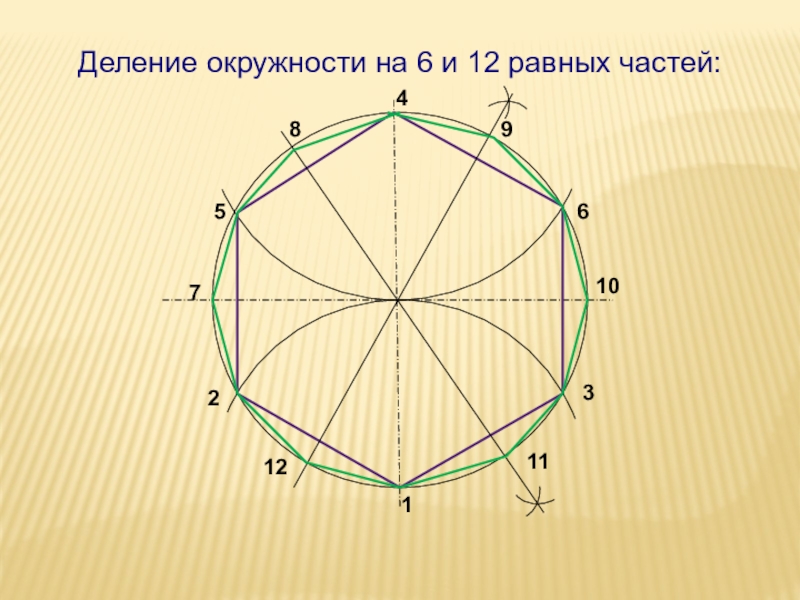
- 37. 132456789101112Деление окружности на 6 и 12 равных частей:
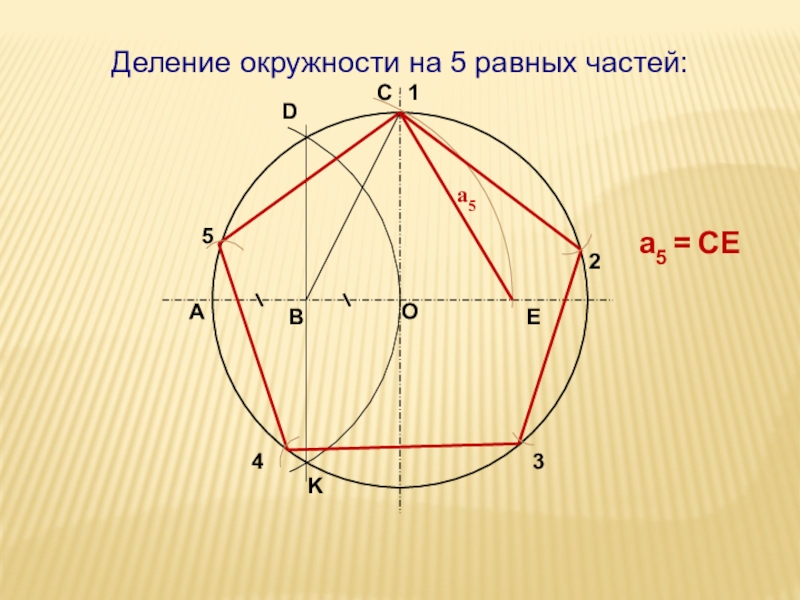
- 38. 1234ОАBС а5DЕа5 = СЕ K5Деление окружности на 5 равных частей:
- 39. 1234ОАВЕ5а10 = ОЕа10 Деление окружности на 10 равных частей:
- 40. 1234ОАВD5а7 = ВДа767Деление окружности на 7 равных частей:
- 41. Алгоритм деления окружности на любое количество равных
- 42. Алгоритм деления окружности на любое количество равных частей:
- 43. Алгоритм деления окружности на любое количество равных
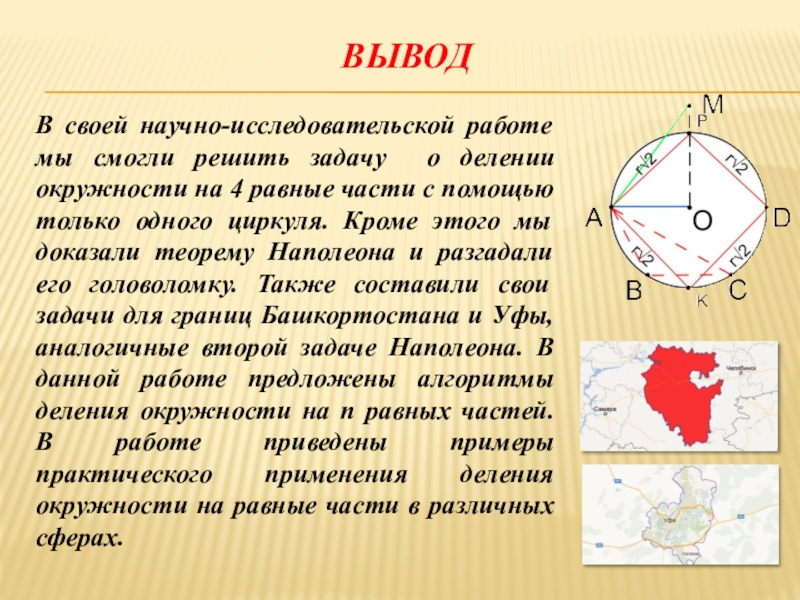
- 44. ВЫВОД В своей научно-исследовательской работе мы смогли
- 45. Практическое значение работы:Изучение задач Наполеона расширяет кругозор
- 46. ЗаключениеКарл Фридрих ГауссЗадача деление окружности эквивалентна решению
Наполеоне Буонапарте (1769—1821)
Слайд 1“Задачи Наполеона”
Гайсина Рита Рамилевна
Иванова Надежда Владимировна
МАОУ Лицей №58 г. Уфа
Слайд 3
Цель работы:
Изучить задачи Наполеона
и найти способ решения задачи о
делении
окружности на четыре
равные части с помощью
только одного циркуля
равные части с помощью
только одного циркуля
Слайд 4
Задачи:
1) Изучить соответствующую историческую и математическую литературу.
2) Изучить задачи и
головоломки Наполеона.
3) Решить задачу Наполеона о делении окружности на четыре равные части с помощью только одного циркуля.
4) Найти алгоритм деления окружности на равные части с помощью циркуля и линейки.
5) Показать практическое применение деления окружности на равные части.
3) Решить задачу Наполеона о делении окружности на четыре равные части с помощью только одного циркуля.
4) Найти алгоритм деления окружности на равные части с помощью циркуля и линейки.
5) Показать практическое применение деления окружности на равные части.
Слайд 5В своей работе мы выдвинули следующее предположение: можно ли разделить окружность
на четыре части не прибегая к линейке
(одна из задач Наполеона).
(одна из задач Наполеона).
Слайд 6Если на каждой стороне произвольного треугольника построить по равностороннему треугольнику, то
треугольник с вершинами в центрах равносторонних треугольников — тоже равносторонний.
Теорема Наполеона:
Слайд 7На сторонах треугольника построим во внешнюю его сторону равносторонние треугольники.
Вот как
это выглядит в движении.
Слайд 9Центры равносторонних треугольников равноудалены друг от друга.
Зеленый треугольник всегда равносторонний.
Слайд 11∠AO1С = ∠BO2А = ∠СО3В = 120°
∠O1СO3 + ∠О1АO2 + ∠O2ВO3 = 360°
O1,
O2 и O3 - центры равносторонних треугольников
AO1 = O1С, ВO3 = O3C, BО2 = O2А
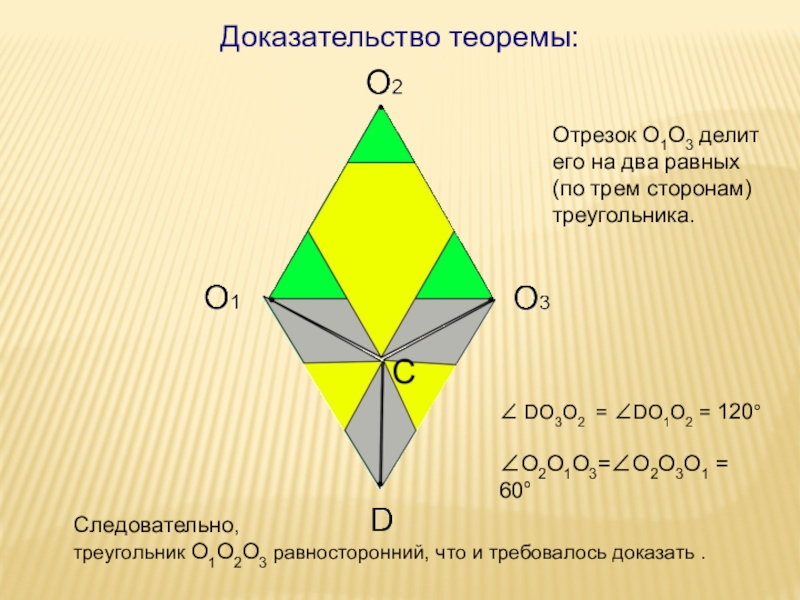
Доказательство теоремы:
Слайд 12Выделим шестиугольник АO2ВO3СO1 ,а внешние к нему невыпуклые четырехугольники отбросим
Отрезаем от
шестиугольника треугольники О2АО1 и O2ВO3, перемещая их в плоскости, получаем четырехугольник O2O1DO3.
Доказательство теоремы:
Слайд 13
Доказательство теоремы:
Следовательно,
треугольник O1O2O3 равносторонний, что и требовалось доказать .
∠ DO3O2 =
∠DO1O2 = 120°
∠O2O1O3=∠O2O3O1 = 60°
Отрезок O1O3 делит его на два равных (по трем сторонам) треугольника.
Слайд 14Если на сторонах параллелограмма построить вовне квадраты, то их центры образуют
квадрат.
Обобщенная теорема Наполеона
(Теорема Тебо):
Слайд 15Флаг Израиля
Следствие теоремы Наполеона:
Звезда Давида — эмблема в форме шестиконечной звезды
(гексаграммы), в которой два равносторонних треугольника наложены друг на друга: верхний — вершиной вверх, нижний — вершиной вниз, образуя структуру из шести равносторонних треугольников, присоединённых к сторонам шестиугольника.
Слайд 16Одно из 7 чудес света - египетские пирамиды. Самая знаменитая из
них - пирамида Хеопса высотой 147 м, в основании которой квадрат со стороной 233 м. Если из каменных блоков пирамиды возвести стену толщиной 20 см вокруг Франции, то какова будет высота этой стены?
Задача Наполеона о пирамиде Хеопса:
Слайд 17Ответ: 2 метра 66 сантиметров
Дано:
h 1 = 147 м
S = 233
м
h = 20 см
L = 5000 км
h = 20 см
L = 5000 км
Найти:
H - ?
СИ:
h = 0,2 м
L = 5.000.000 м
Решение:
V = 1/3*S*h
V = 1/3*233*233*147
= 2660161 м^3
H стены = V/Lh
H стены =
2660161/ 5.000.000 *0,2 = 2,66 м
Решение задачи Наполеона:
Слайд 18Одно из 7 чудес света - египетские пирамиды. Самая знаменитая из
них - пирамида Хеопса высотой 147 м, в основании которой квадрат со стороной 233 м. Если из каменных блоков пирамиды возвести стену толщиной 20 см вокруг Башкортостана, то какова будет высота этой стены?
Задача:
Слайд 19Ответ: 5 метра 32 сантиметра
Дано:
h 1 = 147 м
S = 233
м
h = 20 см
L = 2500 км
h = 20 см
L = 2500 км
Найти:
H - ?
СИ:
h = 0,2 м
L = 2.500.000 м
Решение:
V = 1/3*S*h
V = 1/3*233*233*147
= 2660161 м^3
H стены = V/Lh
H стены =
2660161/ 2.500.000 *0,2 = 5,32 м
Решение задачи:
Слайд 20Одно из 7 чудес света - египетские пирамиды. Самая знаменитая из
них - пирамида Хеопса высотой 147 м, в основании которой квадрат со стороной 233 м. Если из каменных блоков пирамиды возвести стену толщиной 20 см вокруг Уфы, то какова будет высота этой стены?
Задача:
Слайд 21Ответ: 57 метра 33 сантиметра
Дано:
h 1 = 147 м
S = 233
м
h = 20 см
L = 232 км
h = 20 см
L = 232 км
Найти:
H - ?
СИ:
h = 0,2 м
L =
232.000 м
Решение:
V = 1/3*S*h
V = 1/3*233*233*147
= 2660161 м^3
H стены = V/Lh
H стены =
2660161/ 232000*0,2 =57,33 м
Решение задачи:
Слайд 26По преданию Наполеон Бонапарт предложил итальянскому математику Лоренцо Маскерони задачу. Известно
также, что во время беседы с Лагранжем и Лапласом (знаменитыми французскими математи-ками) Наполеон поразил их. Он объяснил им некоторые из предложенных Маскерони решений следующей его задачи.
Слайд 27По преданию Наполеон Бонапарт предложил итальянскому математику Лоренцо Маскерони задачу. Известно
также, что во время беседы с Лагранжем и Лапласом (знаменитыми французскими математи-ками) Наполеон поразил их. Он объяснил им некоторые из предложенных Маскерони решений следующей его задачи.
Слайд 28По преданию Наполеон Бонапарт предложил итальянскому математику Лоренцо Маскерони задачу. Известно
также, что во время беседы с Лагранжем и Лапласом (знаменитыми французскими математи-ками) Наполеон поразил их. Он объяснил им некоторые из предложенных Маскерони решений следующей его задачи.
Слайд 29Данную окружность разделить на четыре равные части, не прибегая к линейке.
Положение центра окружности дано.
Задача Наполеона:
Слайд 301) Анализ задачи.
Разделить окружность на четыре части , значит вписать в
эту
окружность квадрат со стороной а =
окружность квадрат со стороной а =
Решение задачи:
.
Слайд 331) АС из АВС по теореме косинусов
АC =
2)
АМО прямоугольный т.к. АМД равнобедренный, а МО медиана и высота.
2) ОМ из АМО по теореме Пифагора
ОМ = =
3) AP=AK = ОМ =
(как радиусы окружности (А, ОМ))
Так AD диаметр данной окружности (по построению),
следовательно, AP=PD=DK=AK=
2) ОМ из АМО по теореме Пифагора
ОМ = =
3) AP=AK = ОМ =
(как радиусы окружности (А, ОМ))
Так AD диаметр данной окружности (по построению),
следовательно, AP=PD=DK=AK=
3) Доказательство.
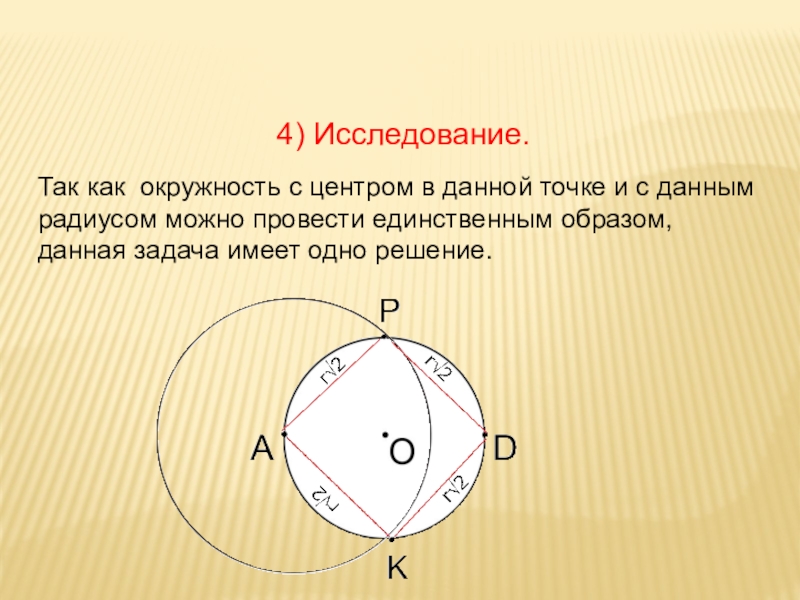
Слайд 34Так как окружность с центром в данной точке и с данным
радиусом можно провести единственным образом,
данная задача имеет одно решение.
4) Исследование.
Слайд 41
Алгоритм деления окружности
на любое количество равных частей:
Где k - коэффициент
длины хорды, которую циркулем откладывают на заданной окружности n раз;
D – диаметр.
D – диаметр.
Слайд 43
Алгоритм деления окружности
на любое количество равных частей:
program abc;
Var n,a,R:real;
begin
writeln('Введите число
n');
readln(n);
writeln('Введите радиус окружности R');
readln(R);
a:=2*R*sin(Pi/n);
writeln('Сторона правильного многоугольника равна ',a:3:1);
end.
readln(n);
writeln('Введите радиус окружности R');
readln(R);
a:=2*R*sin(Pi/n);
writeln('Сторона правильного многоугольника равна ',a:3:1);
end.
Слайд 44ВЫВОД
В своей научно-исследовательской работе мы смогли решить задачу о делении окружности
на 4 равные части с помощью только одного циркуля. Кроме этого мы доказали теорему Наполеона и разгадали его головоломку. Также составили свои задачи для границ Башкортостана и Уфы, аналогичные второй задаче Наполеона. В данной работе предложены алгоритмы деления окружности на n равных частей. В работе приведены примеры практического применения деления окружности на равные части в различных сферах.
Слайд 45Практическое значение работы:
Изучение задач Наполеона расширяет кругозор и развивает логическое мышление.
Алгоритмы деления окружности на n частей применяются на уроках черчения, начертательной геометрии в ВУЗах.
Слайд 46Заключение
Карл Фридрих Гаусс
Задача деление окружности эквивалентна решению двучленного уравнения:
xn — 1
= 0
Деление окружности при помощи циркуля и линейки возможно только тогда, когда все корни этого уравнения можно получить последовательным решением квадратных и линейных уравнений.
Деление окружности при помощи циркуля и линейки возможно только тогда, когда все корни этого уравнения можно получить последовательным решением квадратных и линейных уравнений.
