- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике по теме: Введение в комбинаторику
Содержание
- 1. Презентация по математике по теме: Введение в комбинаторику
- 2. Тип урока: урок изучения нового материала с
- 3. Ход урока: Организационный моментПостановочно – практическое задание.Историческая
- 4. КОМБИНАТОРИКА – РАЗДЕЛ МАТЕМАТИКИ, ИЗУЧАЮЩИЙ КОМБИНАЦИИ И ПЕРЕСТАНОВКИ ПРЕДМЕТОВ.
- 5. Историческая справка:
- 6. Христиа́н Гю́йгенс ван Зёйлихем (14 апреля 1629—
- 7. Пьер-Симо́н Лапла́с (23 марта 1749 — 5
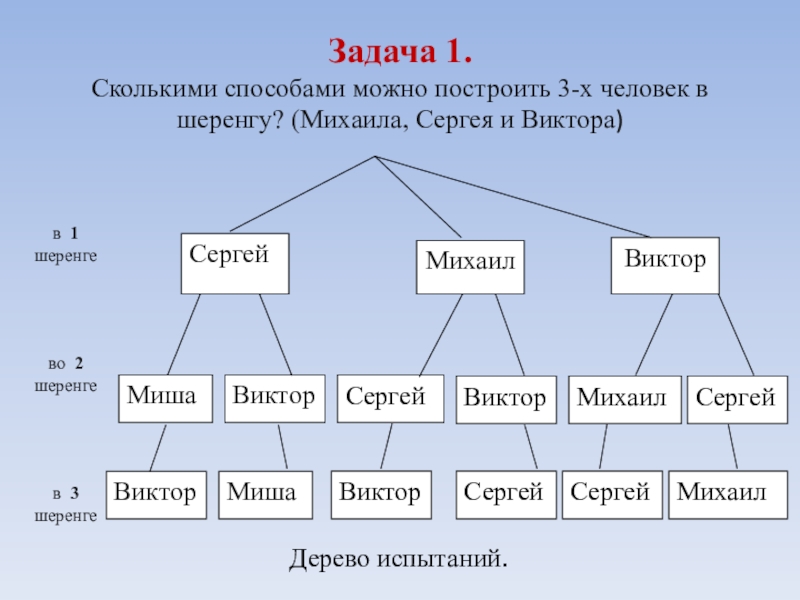
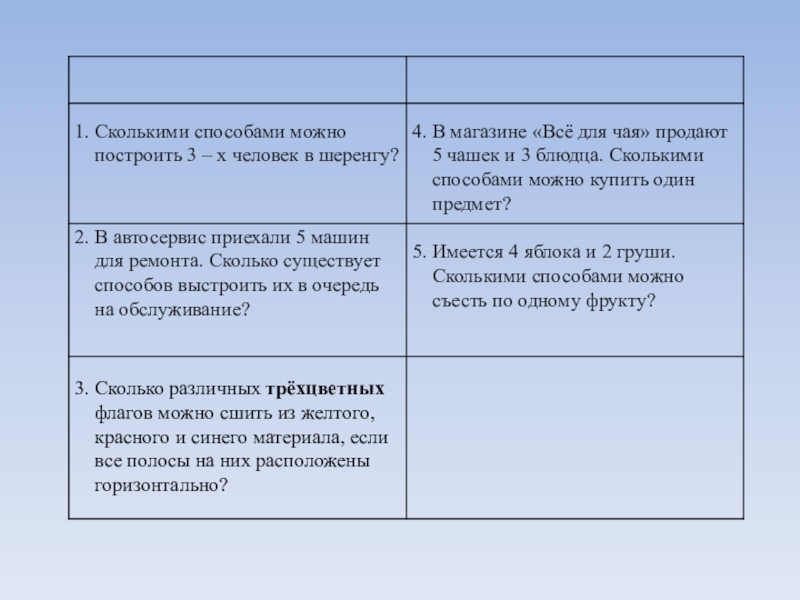
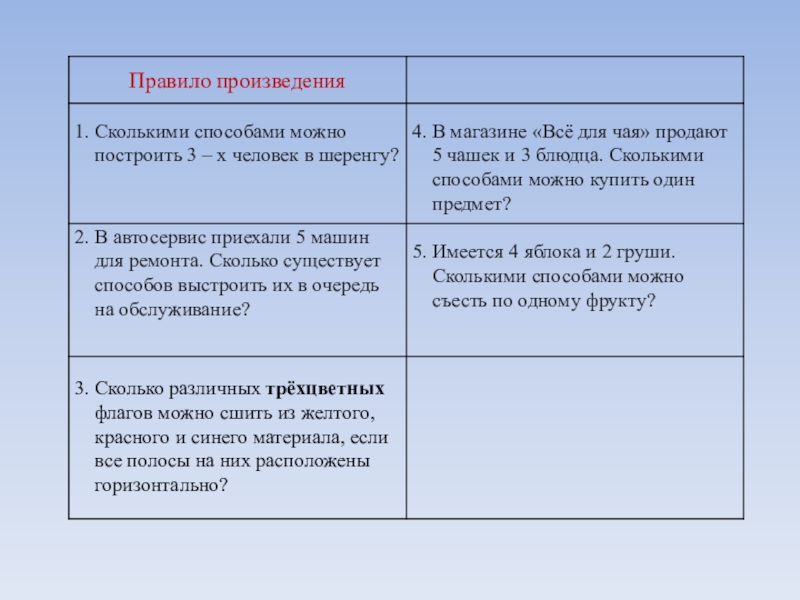
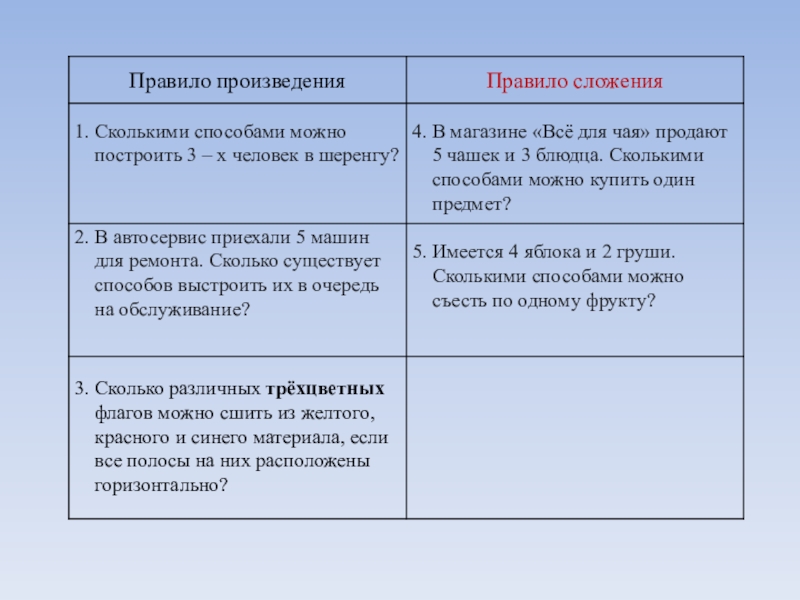
- 8. Задачи.Сколькими способами можно построить 3 – х
- 9. Слайд 9
- 10. 4. В магазине «Всё для чая»
- 11. в 1 шеренге во 2 шеренгев
- 12. Второй способ оформленияСпособы: М С ВМ В
- 13. Задача 2.В автосервис приехали 5 машин для
- 14. Сколько различных трёхцветных флагов можно сшить из
- 15. Задача 4.В магазине «Всё для чая» продают
- 16. Задача 5.Имеется 4 яблока и 2 груши.
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Китай XIX векСценка
- 21. Слайд 21
Слайд 2Тип урока: урок изучения нового материала с элементами игры и
Цели урока:
Образовательная:
создать условия для формирования понятия о науке «Комбинаторика»,
о истории ее возникновения.
Деятельностная:
обучающиеся получат возможность научится решать несложные комбинаторные задачи.
Задачи урока:
Образовательная:
дать понятие способов решения комбинаторных задач (дерево испытаний, перебор),
определить правило умножения и правило сложения.
Воспитательная:
воспитание трудолюбия;
создание условий для творческой самореализации личности.
Развивающая:
развитие познавательного интереса, логического мышления и внимания.
Оборудование:
Мультимедийное оборудование;
Демонстрационные файлы;
Раздаточный материал для работы в классе;
Раздаточный материал для домашнего задания.
Слайд 3Ход урока:
Организационный момент
Постановочно – практическое задание.
Историческая справка.
Практические задания:
Рассмотрение примеров
I вариант
Решить задачи по шаблонам;
II вариант
Решить задачу;
Составить условие задачи по схеме и решить её.
Домашнее задание (устный разбор задачи).
Подведение итогов урока.
Слайд 5Историческая справка:
Блез Паска́ль (19 июня 1623
Никколо Тарталья (1499—1557) составил таблицу, показывавшую, сколькими способами могут выпасть r костей. Однако при этом не учитывалось, что одна и та же сумма очков может быть получена разными способами.
Слайд 6
Христиа́н Гю́йгенс ван Зёйлихем (14 апреля 1629— 8 июля 1695)
Яков (Якоб) Бернулли (27.12.1654 — 16.08.1705)
Абрахам де Муавр (26 мая 1667—27 ноября 1754)
Слайд 7
Пьер-Симо́н Лапла́с (23 марта 1749 — 5 марта 1827)
(30 апреля 1777— 23 февраля 1855)
Слайд 8Задачи.
Сколькими способами можно построить 3 – х человек в шеренгу? (Михаила,
На первой полке в 2 раза больше книг, чем на второй. Когда с первой полки переставили на вторую 12 книг, на обеих полках стало поровну. Сколько книг было на каждой полке?
В автосервис приехали 5 машин для ремонта. Сколько существует способов выстроить их в очередь на обслуживание?
За 8 часов по течению лодка проходит расстояние, в 2 раза больше, чем за 5 часов против течения. Какова скорость течения, если собственная скорость лодки 13,5 км/ч?
Сколько различных трёхцветных флагов можно сшить из желтого, красного и синего материала, если все полосы на них расположены горизонтально?
Слайд 104. В магазине «Всё для чая»
продают 5
Сколькими способами можно
купить один предмет?
5. Имеется 4 яблока и 2 груши.
Сколькими способами
можно съесть по одному фрукту?
Слайд 11
в 1 шеренге
во 2 шеренге
в 3 шеренге
Задача 1.
Сколькими способами
Дерево испытаний.
Слайд 12Второй способ оформления
Способы:
М С В
М В С
С В М
С М
В С М
В М С
6 способов: 3∙2∙1=6
Перебор
Задача 1.
Слайд 13Задача 2.
В автосервис приехали 5 машин для ремонта. Сколько существует способов
Решение:
5∙4∙3∙2∙1=120
Ответ:
120 способов
Слайд 14Сколько различных трёхцветных флагов можно сшить из желтого, красного и синего
Ответ:
Задача 3.
Слайд 15Задача 4.
В магазине «Всё для чая» продают 5 чашек и 3
Решение:
Чашку – 5
Блюдце – 3
5 + 3 = 8(способов)
Ответ: 8
Слайд 16Задача 5.
Имеется 4 яблока и 2 груши. Сколькими способами можно съесть
Решение:
Яблоко – 4
Грушу – 2
4 + 2 = 6 (способов)
Ответ: 6