- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике по теме Устный счет ПРОСТО!
Содержание
- 1. Презентация по математике по теме Устный счет ПРОСТО!
- 2. ПланПризнаки делимостиХитрости сложного умноженияМатематические фокусыУмножение на 11Умножение
- 3. М.В. Ломоносов "Математику уже затем учить следует, что она ум в порядок приводит "
- 4. 1. Признаки делимости. Чтобы понять,
- 5. Признак делимости на 2. Число делится
- 6. Признак делимости на 4. Число делится
- 7. Признак делимости на 9.Признак делимости на 8. Число
- 8. Признак делимости на 11.Число делится на 11,
- 9. В истории математики известно много
- 10. Умножение двузначного числа на 11. Пусть,
- 11. Умножение
- 12. Легкое
- 13. Умножение
- 14. Умножение
- 15. Возведение в квадрат числа, оканчивающегося на цифру
- 16. 3 Фокусы УГАДАННЫЙ ДЕНЬ РОЖДЕНИЯНаписать на бумажке
- 17. УГАДАННЫЙ ВОЗРАСТУмножить число своих лет на 10.
- 18. Волшебная таблицаЗадумать любое число из таблицы.Указать, в
Слайд 2План
Признаки делимости
Хитрости сложного умножения
Математические фокусы
Умножение на 11
Умножение на 111 двузначного числа
На 9 (легкий способ)
На 9, 99, 999
На 101 двузначного числа
Возведение в квадрат числа, оканчивающегося на цифру 5
На 2
На 3
На 5
На 6
На 8
На 9
На 11
Угаданный день рождения
Угаданный возраст
Волшебная таблица
Слайд 41. Признаки делимости.
Чтобы понять, делится ли одно число
Слайд 5Признак делимости на 2.
Число делится на 2, если его
делится на 2 или является нулём (то есть число четное).
Признак делимости на 3.
Число делится на 3, если сумма всех его цифр
делится на 3.
Слайд 6Признак делимости на 4.
Число делится на 5, если его
Признак делимости на 5.
Число делится на 4, если две его последние цифры нули или образуют число, делящееся на 4.
Признак делимости на 6.
Число делится на 6, если оно делится одновременно на 2 и на 3.
Слайд 7Признак делимости на 9.
Признак делимости на 8.
Число делится на 8, если
Число делится на 9, если сумма всех его цифр делится на 9.
Слайд 8Признак делимости на 11.
Число делится на 11, если сумма цифр, которые
четных местах равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11.
В самом деле, признак делимости на 11
очень интересен, попробуем разобраться
на примере:
Проверим, делится ли 671 на 11.
Итак, цифры которые стоят на нечетных местах, это 6 (стоит на первом месте) и 1 (стоит на третьем месте). Цифра, которая стоит на четном месте, это 7 (стоит на втором месте). 6 + 1 = 7. Сумма цифр стоящих на нечетном месте равна сумме цифр на четном месте, значит, 671 делится на 11.
Слайд 9 В истории математики известно много способов умножения, отличающихся либо
2. Хитрости сложного умножения.
Слайд 10Умножение двузначного числа на 11.
Пусть, надо умножить 27 •
Достаточно сложить эти две цифры 2 + 7 = 9, поставить итог между ними, и мы получим ответ: 27 • 11 = 297. При сложении, разумеется, может получиться начинающееся
с 1 двузначное число.
Тогда эту единицу надо прибавить к цифре десятков, а в середину вставлять только цифру единиц суммы.
34•11=374
85•11=935
Слайд 11
Умножение на 111 двузначного числа с суммой цифр меньше 10.
52•111= 5 (между цифрами дважды вставляем сумму 5+2=7) 2 =5772.
Слайд 12
Легкое умножение на 9
однозначного числа .
Положите обе руки
Пусть каждый палец по порядку означает соответствующее число: первый слева – 1, второй за ним – 2, третий – 3 и т.д. до десятого, который означает 10. Требуется теперь умножить любое из первых десяти чисел на 9. Для этого вам стоит только, не сдвигая рук со стола, приподнять вверх тот палец, который обозначает множимое. Тогда остальные пальцы, лежащие налево от поднятого пальца, дадут в сумме число десятков, а пальцы направо – число единиц.
Слайд 13
Умножение на 9, 99, 999.
Для того, чтобы найти произведение
8•9=72
46•99=4554
137•999=136863
Слайд 14
Умножение двузначного числа на 101.
Нужно мысленно приписать
Пример:
52•101= 5252.
74•101= 7474.
Слайд 15Возведение в квадрат числа, оканчивающегося на цифру 5
35•35=1225
Число десятков умножают на
45•45=2025
75•75=5625
Слайд 163 Фокусы
УГАДАННЫЙ ДЕНЬ РОЖДЕНИЯ
Написать на бумажке секретно число своего дня рождения.
Умножить
Сложить получившееся произведение и число 5.
Умножить на 50 полученную сумму.
К этому результату необходимо прибавить номер месяца рождения (июль — 7, январь — 1).
Вслух назвать полученное число.
Через секунду фокусник называет день и месяц рождения зрителя.
Слайд 17УГАДАННЫЙ ВОЗРАСТ
Умножить число своих лет на 10.
Любое однозначное число умножить
Из первого произведения вычесть второе и сообщить полученную разность.
Через секунду фокусник называет возраст зрителя.
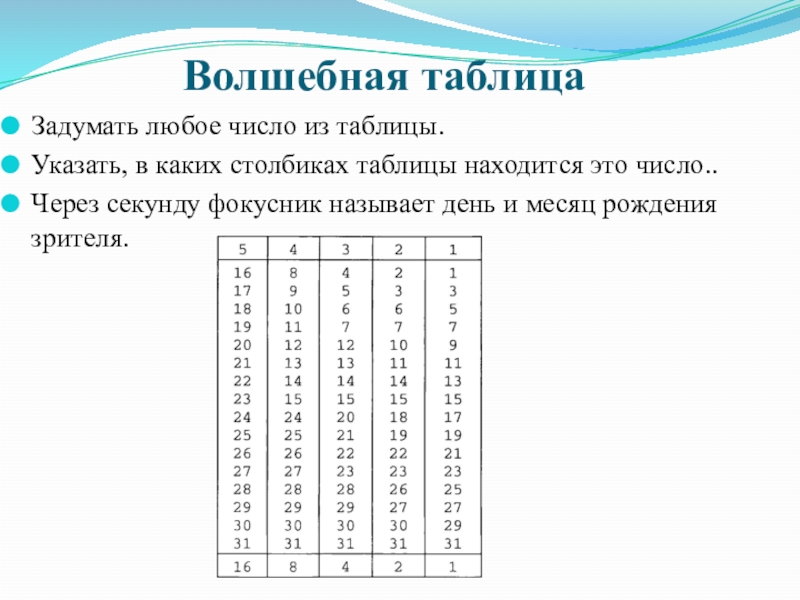
Слайд 18Волшебная таблица
Задумать любое число из таблицы.
Указать, в каких столбиках таблицы находится
Через секунду фокусник называет день и месяц рождения зрителя.