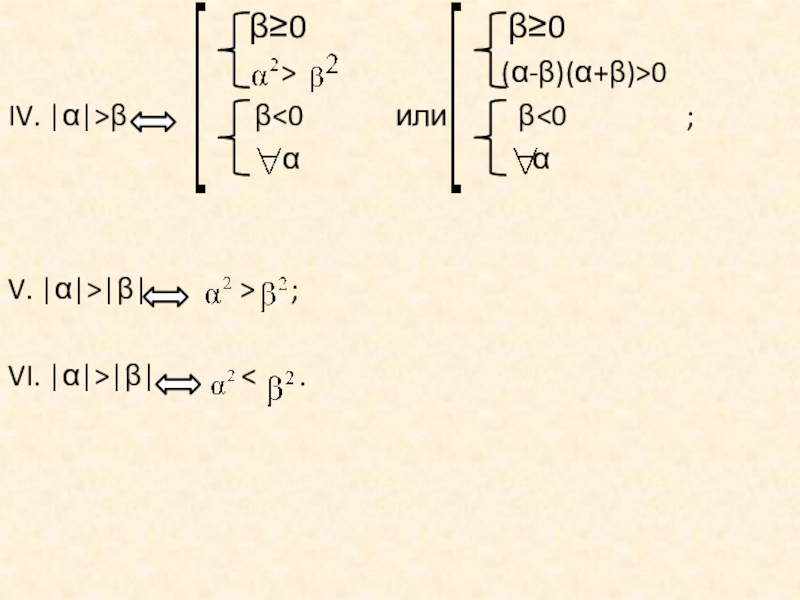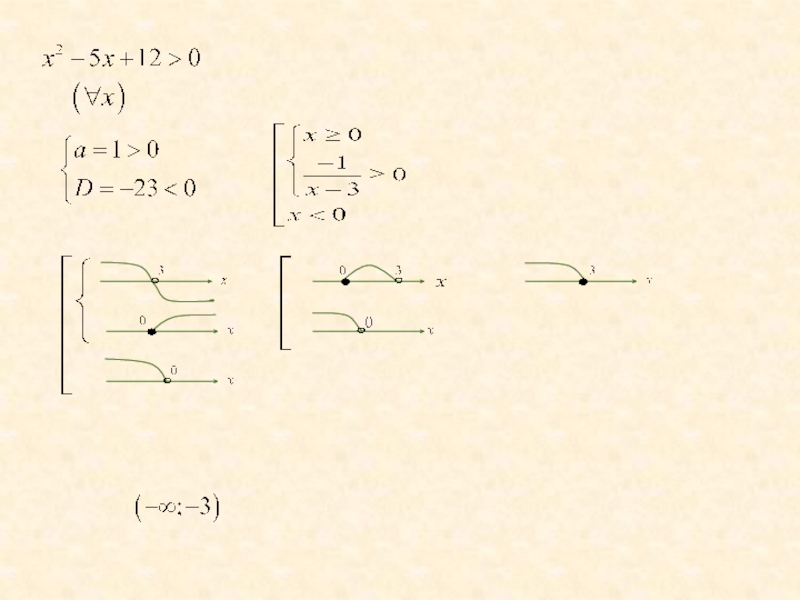- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике по теме Модуль
Содержание
- 1. Презентация по математике по теме Модуль
- 2. Введение Работа «модуль» предназначена для
- 3. Цель работы: На основе коррекции базовых
- 4. З а д а ч иАкцентировать внимание
- 5. Определение модуля.Свойства модульныхнеравенств
- 6. 1. Модулем (абсолютной величиной) действительного числа α
- 7. Свойства модульных неравенств
- 8. Слайд 8
- 9. Применение определения модуля и свойств модульных неравенств
- 10. Иррациональные выражения с модулем 1
- 11. Функции с модулем Найдите сумму всех
- 12. Практикум по решению модульных неравенств
- 13. Решение иррациональных выражений с модулемПример 1:
- 14. Решение иррациональных выражений с модулемПример 2Преобразуем подкоренные выражения:
- 15. Решение иррациональных выражений с модулемПример 3:
- 16. Решение иррациональных уравнений с модулямиПример 4:Представим выражение
- 17. Функции с модулемПример 1.Решение:
- 18. Функции с модулемПример 2Решение:Преобразуем неравенство и применим свойство:
- 19. Функции с модулемПример 3Решение:Преобразуем неравенство и применим свойство:
- 20. Построение графиков функцииПример 1. Построить график функции
- 21. Если
- 22. Построение графиков функцийПример 2. Построить график функцииРешение:
- 23. Решение практикума модульных неравенствРассмотрим на примерах, как используются свойства:12
- 24. Решение практикума модульных неравенствРассмотрим на примерах, как
- 25. Решение практикума модульных неравенствРассмотрим на примерах, как
- 26. Решение практикума модульных неравенствРассмотрим на примерах, как
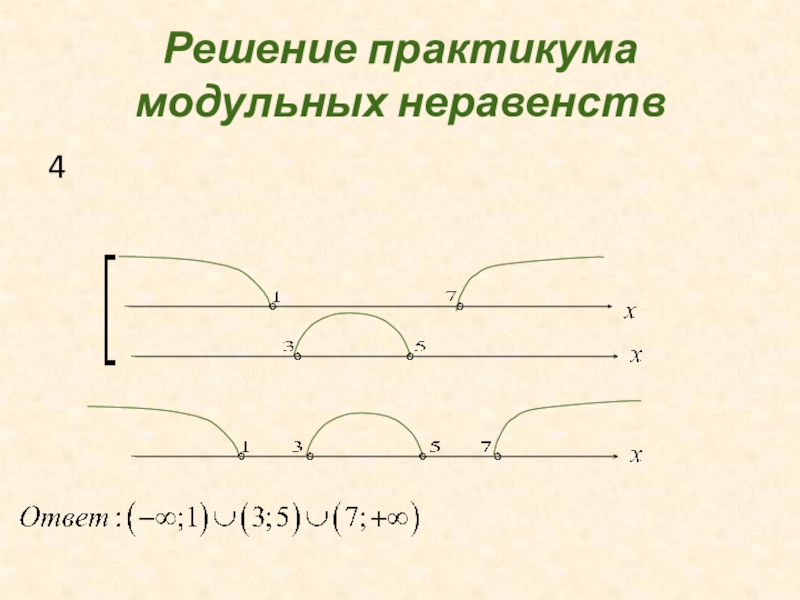
- 27. Решение практикума модульных неравенств4
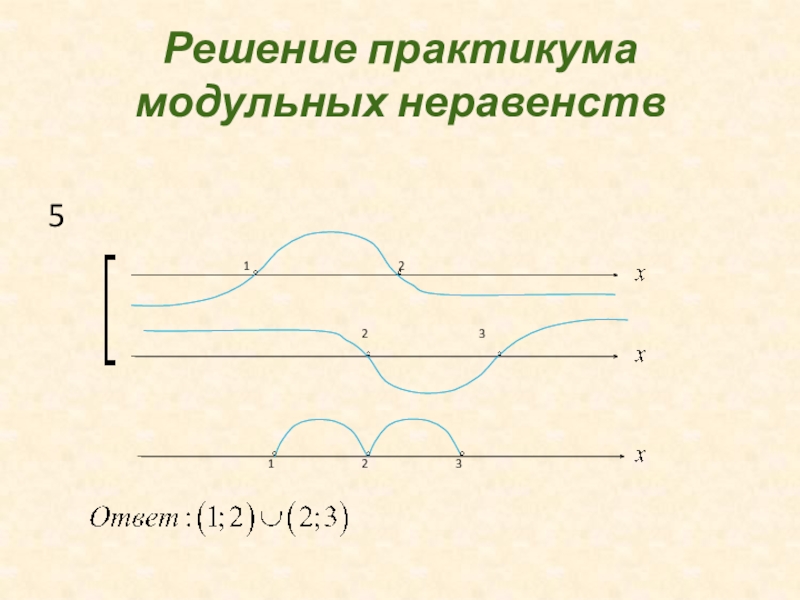
- 28. Решение практикума модульных неравенствРассмотрим на примерах, как используются свойства:5
- 29. Решение практикума модульных неравенств5
- 30. Решение практикума модульных неравенствРассмотрим на примерах, как используются свойства:6
- 31. Решение практикума модульных неравенствРассмотрим на примерах, как
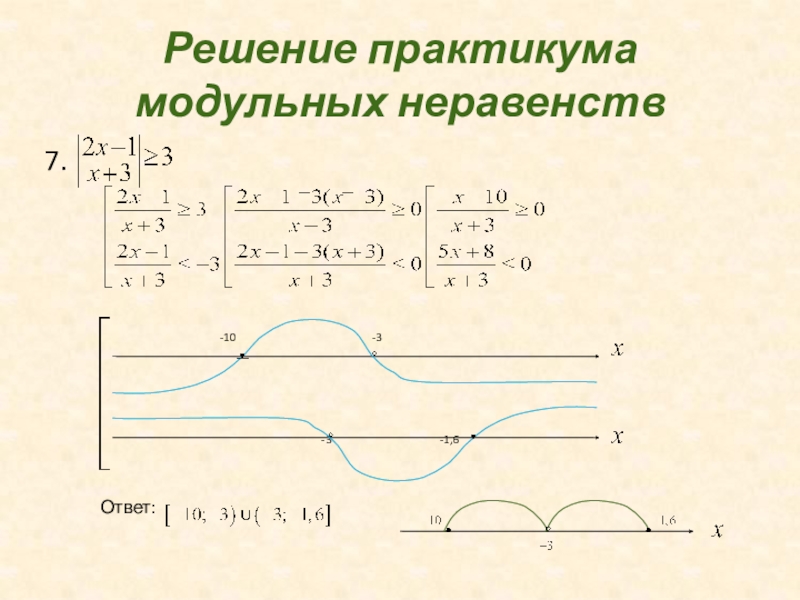
- 32. Решение практикума модульных неравенств7.
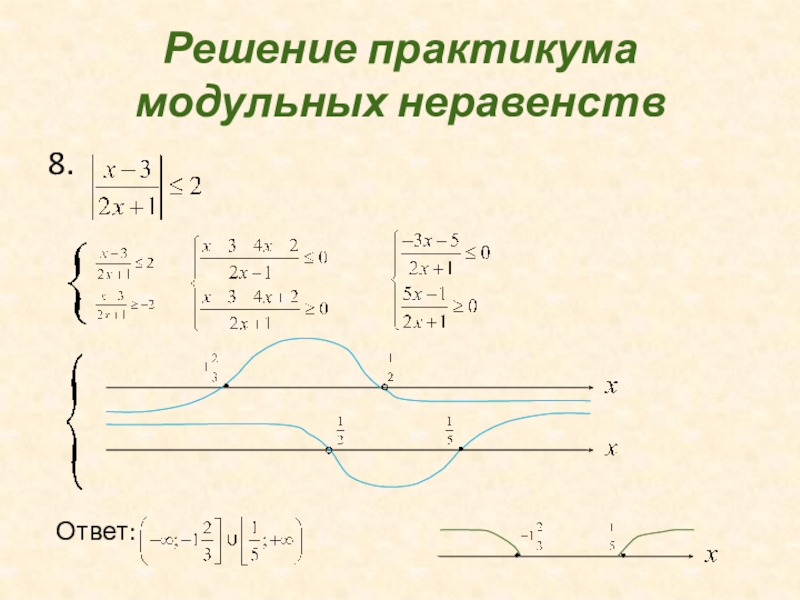
- 33. Решение практикума модульных неравенств8.
- 34. Решение практикума модульных неравенств9.По определению:
- 35. Слайд 35
- 36. Решение практикума модульных неравенств
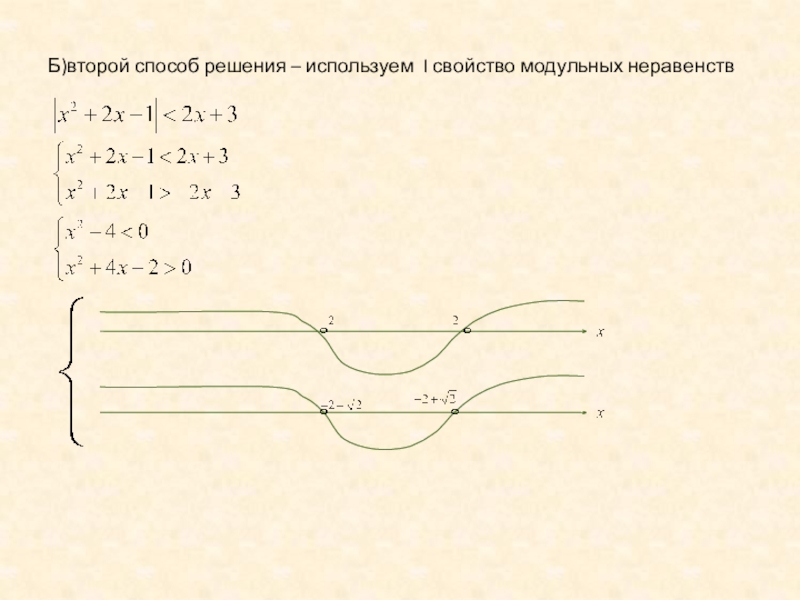
- 37. Б)второй способ решения – используем I свойство модульных неравенств
- 38. Б)второй способ решения – используем I свойство модульных неравенств
- 39. Решение практикума модульных неравенств1 1.а)
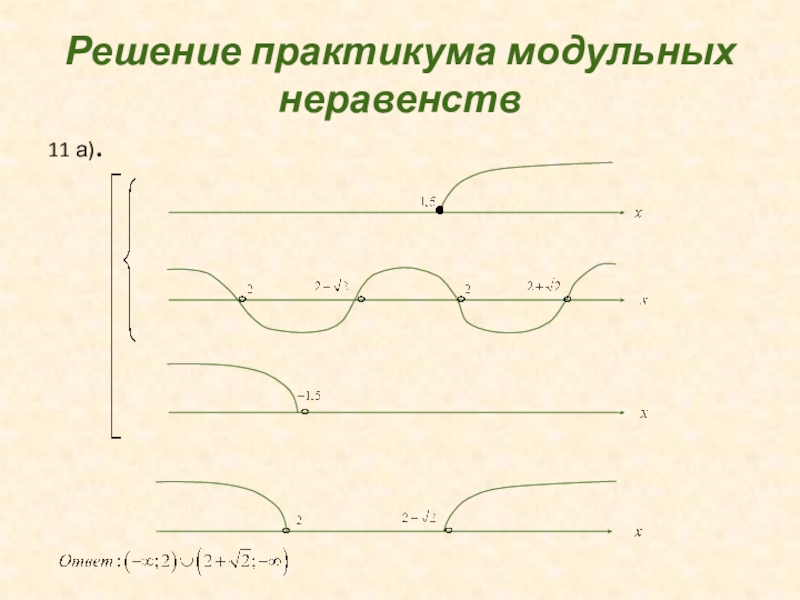
- 40. Решение практикума модульных неравенств11 а).
- 41. Решение практикума модульных неравенств
- 42. Решение практикума модульных неравенств12.Найдем корни модулей:Для решения
- 43. Решение практикума модульных неравенств12.Б)
- 44. Решение практикума модульных неравенств12.В)Ответ:
- 45. Решение практикума модульных неравенств12 г)Объединяя все решения, имеем
- 46. Решение модульных неравенств
- 47. Решение практикума модульных неравенств13 б)
- 48. Слайд 48
- 49. Литература:1.
Введение Работа «модуль» предназначена для повышения эффективности подготовки учащихся 10-11 классов к итоговой аттестации (ЕГЭ) по алгебре и началам анализа за курс полной средней школы и предусматривает их подготовку к дальнейшему математическому образованию.
Слайд 2Введение
Работа «модуль» предназначена для повышения эффективности подготовки учащихся
10-11 классов к итоговой аттестации (ЕГЭ) по алгебре и началам анализа за курс полной средней школы и предусматривает их подготовку к дальнейшему математическому образованию.
Результаты ЕГЭ показывают, что у большинства выпускников школ
по теме «Модуль» пробелы в знаниях. У этого явления вполне объяснимые причины, главные из которых:
понятие модуля изучается в 6 классе, причем вводится только через координатную прямую;
определение модуля не отрабатывается на конкретных заданиях на протяжении курса математики и алгебры 6 – 8 классов, встречается только в теме «Арифметический корень» (8класс).
Задачи на применения определения модуля встречаются во многих темах , поэтому не воспринимается учащимися, как отдельная математическая модель.
Результаты ЕГЭ показывают, что у большинства выпускников школ
по теме «Модуль» пробелы в знаниях. У этого явления вполне объяснимые причины, главные из которых:
понятие модуля изучается в 6 классе, причем вводится только через координатную прямую;
определение модуля не отрабатывается на конкретных заданиях на протяжении курса математики и алгебры 6 – 8 классов, встречается только в теме «Арифметический корень» (8класс).
Задачи на применения определения модуля встречаются во многих темах , поэтому не воспринимается учащимися, как отдельная математическая модель.
Слайд 3Цель работы:
На основе коррекции базовых математических знаний учащихся за
курс 6 – 11 классов совершенствовать математическую культуру и творческие способности учащихся.
Слайд 4З а д а ч и
Акцентировать внимание учащихся на единых требованиях
к правилам оформления различных видов заданий с модулем, включаемых в ЕГЭ.
Научить наглядно представлять процессы, происходящие в заданиях.
Экономить учебное время на оформлении условия и записи пояснений к решению.
Без затруднения применять определение модуля действительного числа.
Уметь пользоваться свойствами модульных неравенств и применять нужное свойство к конкретному условию.
Научить наглядно представлять процессы, происходящие в заданиях.
Экономить учебное время на оформлении условия и записи пояснений к решению.
Без затруднения применять определение модуля действительного числа.
Уметь пользоваться свойствами модульных неравенств и применять нужное свойство к конкретному условию.
Слайд 61. Модулем (абсолютной величиной) действительного числа α называется само это число,
если α≥0, и противоположное число – α, если α<0. Модуль α обозначается |α|. Итак,
α, если α≥0,
|α| =
(-1)∙α, если α<0.
2. Геометрически |α| означает расстояние на координатной прямой от точки, изображающей число α, до начала отсчета.
3. Модуль нуля равен нулю.
4. Если α≠0, то на координатной прямой существуют две точки α и -α, равноудаленные от нуля, модули которых равны.
-α 0 α
α, если α≥0,
|α| =
(-1)∙α, если α<0.
2. Геометрически |α| означает расстояние на координатной прямой от точки, изображающей число α, до начала отсчета.
3. Модуль нуля равен нулю.
4. Если α≠0, то на координатной прямой существуют две точки α и -α, равноудаленные от нуля, модули которых равны.
-α 0 α
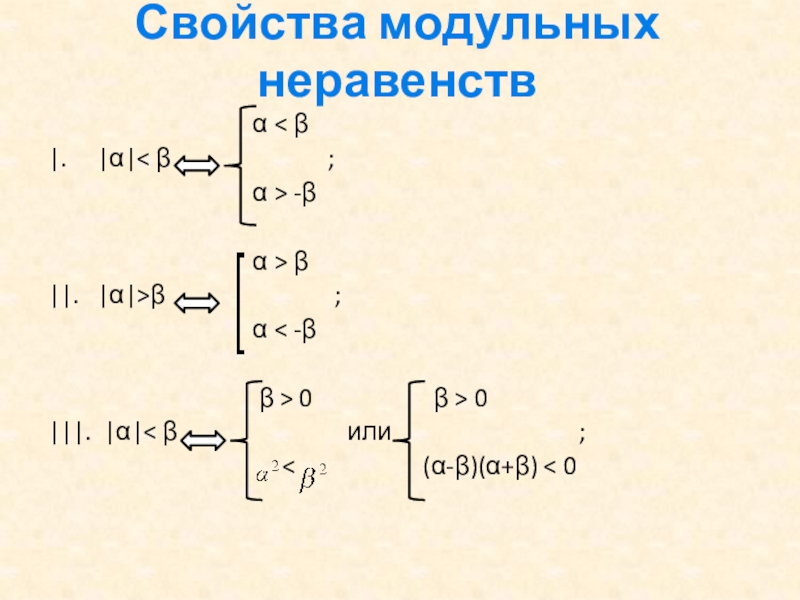
Слайд 7Свойства модульных неравенств
α < β
|. |α|< β ;
α > -β
α > β
||. |α|>β ;
α < -β
β > 0 β > 0
|||. |α|< β или ;
< (α-β)(α+β) < 0
|. |α|< β ;
α > -β
α > β
||. |α|>β ;
α < -β
β > 0 β > 0
|||. |α|< β или ;
< (α-β)(α+β) < 0
Слайд 11Функции с модулем
Найдите сумму всех целых чисел, входящих в
область определения функции:
Построить график функции:
Построить график функции:
Слайд 13Решение иррациональных выражений с модулем
Пример 1:
Представим подкоренное выражение
в виде полного квадрата. В данном случае это возможно:
в условии выражения можно преобразовать следующим образом:
Учитывая, что
и потому получаем:
Ответ: 4.
в условии выражения можно преобразовать следующим образом:
Учитывая, что
и потому получаем:
Ответ: 4.
Слайд 15Решение иррациональных выражений с модулем
Пример 3:
Представим выражение в
виде,
или
Выражение, стоящее под первым знаком, больше 0 при всех допустимых . При значение больше 4, поэтому . Значит и второй знак модуля можно опустить.
Получим: при
Ответ: 4
или
Выражение, стоящее под первым знаком, больше 0 при всех допустимых . При значение больше 4, поэтому . Значит и второй знак модуля можно опустить.
Получим: при
Ответ: 4
Слайд 20Построение графиков функции
Пример 1. Построить график функции
Решение. Перепишем функцию в
таком виде:
, так как .
Если , то функция примет вид:
Если , то функция примет вид:
, так как .
Если , то функция примет вид:
Если , то функция примет вид:
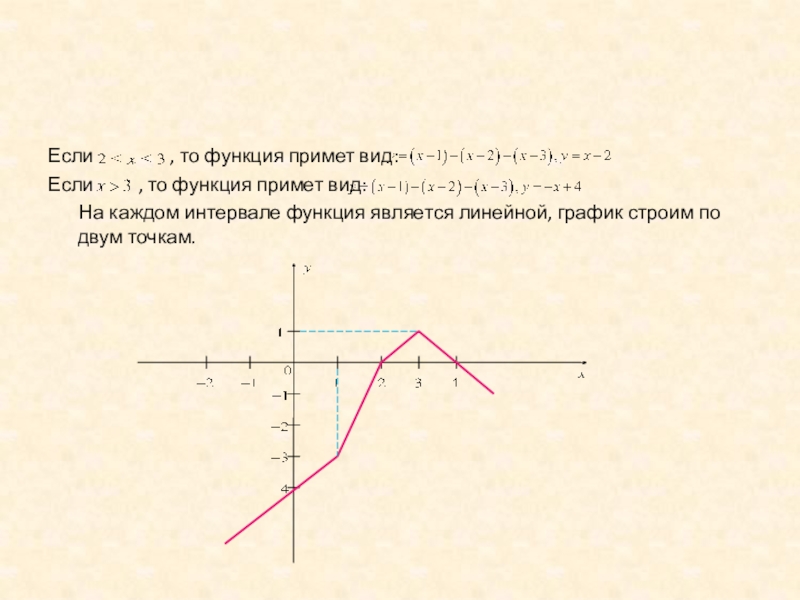
Слайд 21Если , то
функция примет вид:
Если , то функция примет вид:
На каждом интервале функция является линейной, график строим по двум точкам.
Если , то функция примет вид:
На каждом интервале функция является линейной, график строим по двум точкам.
Слайд 22Построение графиков функций
Пример 2. Построить график функции
Решение:
Функция определена
на всей числовой прямой. Графиком является ломаная линия с вершинами в точках, абсциссы которых х = 0, х = 1, а ординаты у(0) = 1, у(1) = 2. Возьмем еще две дополнительные точки
(-1;2), (2;5). Далее строим график функции.
(-1;2), (2;5). Далее строим график функции.
Слайд 24Решение практикума модульных неравенств
Рассмотрим на примерах, как используются свойства:
3
Вначале используем
I свойство
а затем I и II свойства
а затем I и II свойства
Слайд 25Решение практикума модульных неравенств
Рассмотрим на примерах, как используются свойства:
3
-7 -1
X
-5 -3
X
-7 -5 -3 -1
X
X
-5 -3
X
-7 -5 -3 -1
X
Слайд 26Решение практикума модульных неравенств
Рассмотрим на примерах, как используются свойства:
4
Сначала используем
II свойство
Используем свойства I и II
Используем свойства I и II
Слайд 31Решение практикума модульных неравенств
Рассмотрим на примерах, как используются свойства:
6 неравенство можно
решить иначе.
так как обе части неравенства неотрицательны, можно возвести их в квадрат, не нарушая равносильности.
так как обе части неравенства неотрицательны, можно возвести их в квадрат, не нарушая равносильности.
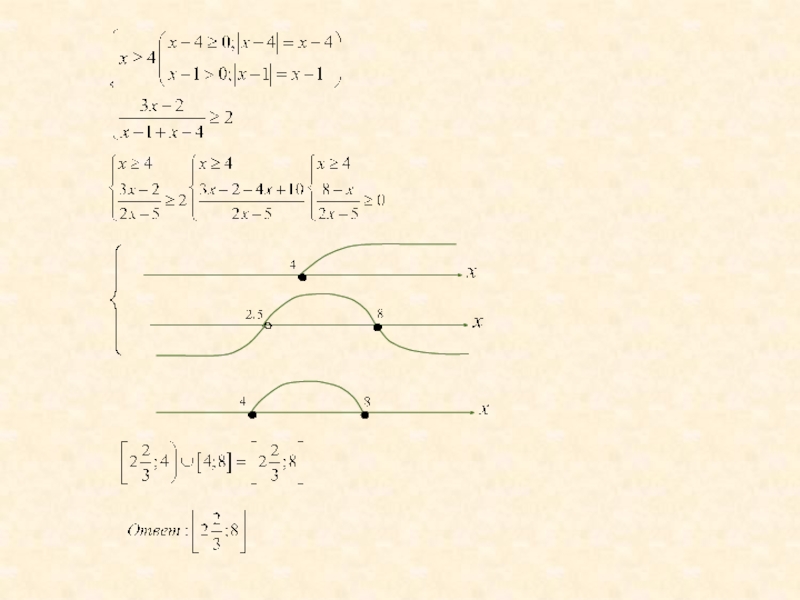
Слайд 42Решение практикума модульных неравенств
12.
Найдем корни модулей:
Для решения такого неравенства рассмотрим его
на каждом интервале отдельно. Корни модулей разбивают числовую ось на интервалы. Учитывая значения подмодульных выражений, раскроем значения модулей на каждом интервале.
А)
А)