«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПРОМЫШЛЕННО-ГУМАНИТАРНЫЙ КОЛЛЕДЖ»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему:Пирамиды (1 курс)
Содержание
- 1. Презентация по математике на тему:Пирамиды (1 курс)
- 2. ОпределениеПирамида – многогранник, составленный из n -
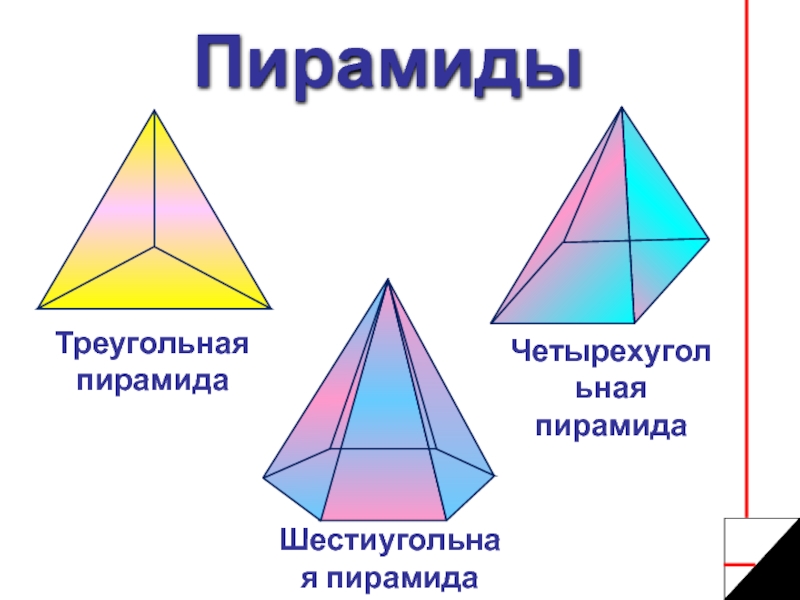
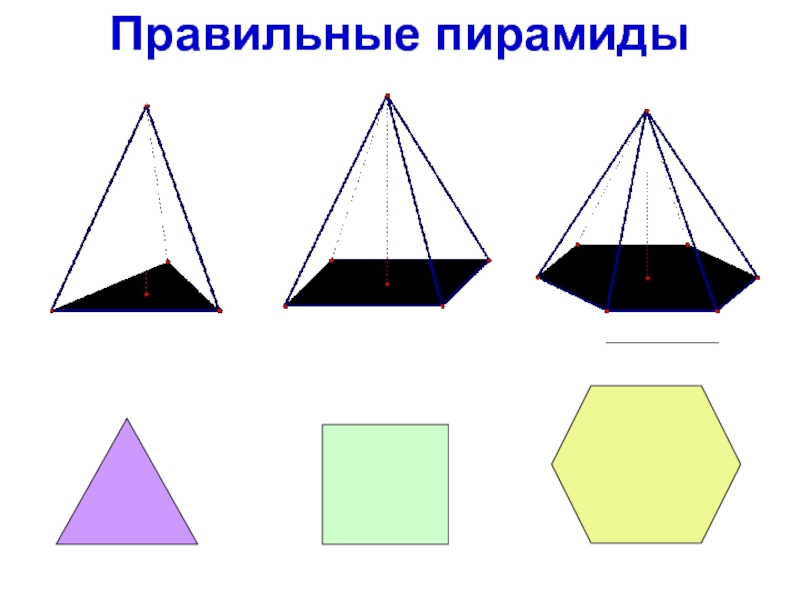
- 3. ПирамидыТреугольная пирамида Шестиугольная пирамидаЧетырехугольная пирамида
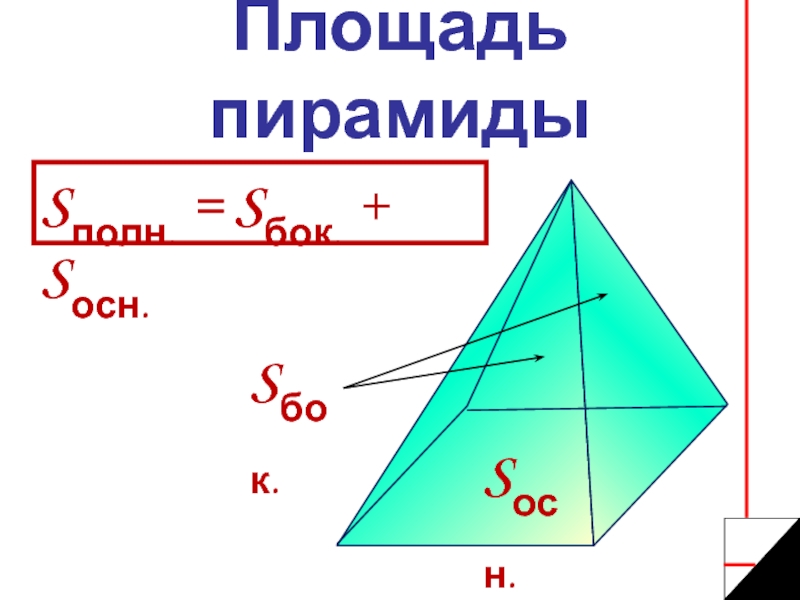
- 4. Площадь пирамидыSполн. = Sбок. + Sосн. Sбок.Sосн.
- 5. Правильная пирамидаПирамида, у которой в основании
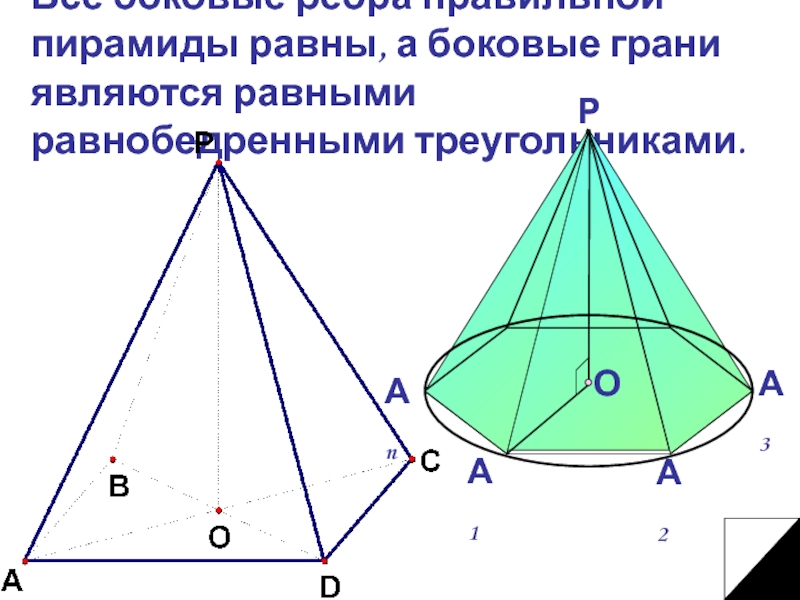
- 6. Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
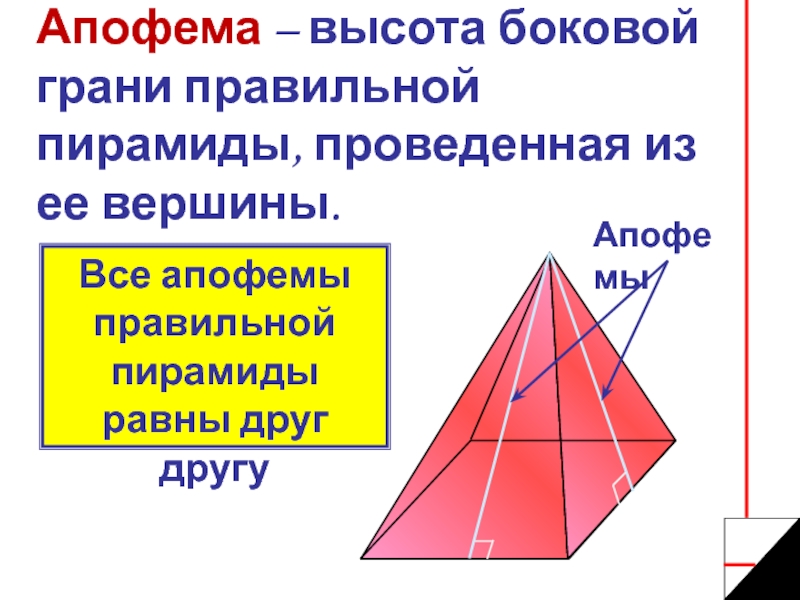
- 7. Апофема – высота боковой грани правильной пирамиды,
- 8. Теорема о площади боковой поверхности правильной
- 9. Правильные пирамиды
- 10. Слайд 10
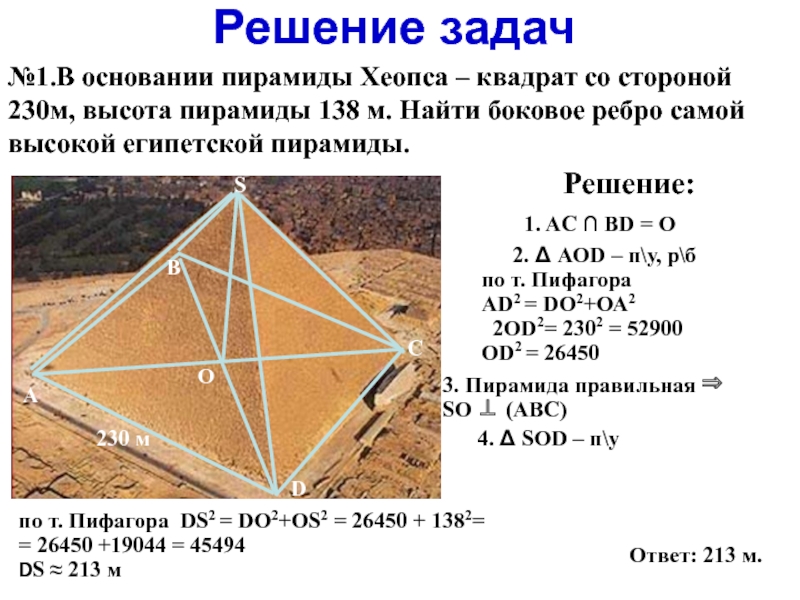
- 11. Решение задачАВСD SО230 м№1.В основании пирамиды Хеопса
- 12. №2. Чему равна площадь поверхности правильного тетраэдра
- 13. 3. (устно) Боковое ребро правильной пирамиды вдвое
- 14. Немного истории Первым из
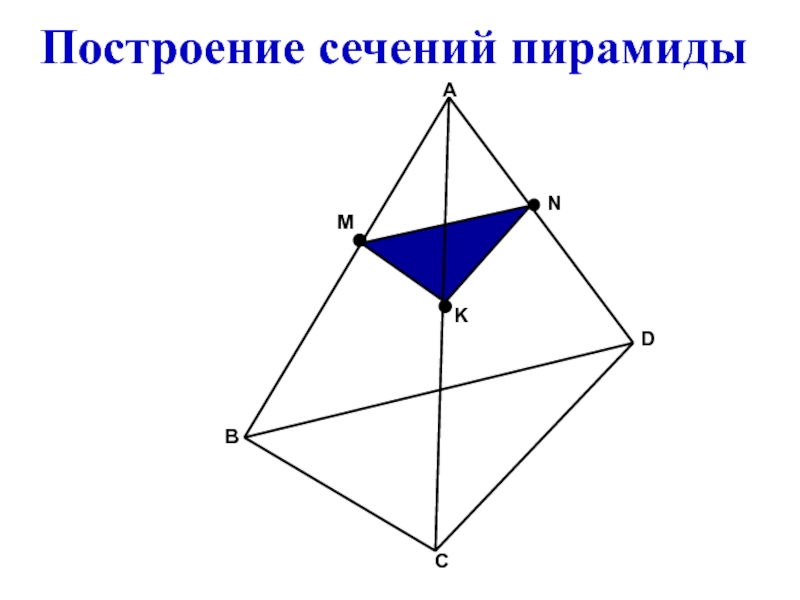
- 15. Построение сечений пирамидыKMNBDCA
- 16. Построение сечения пирамиды1.Построить сечение, проходящее через вершину
- 17. 2. Постройте сечение пирамиды, плоскостью, проходящей через
- 18. Постройте сечение пирамиды, плоскостью, проходящей через заданные
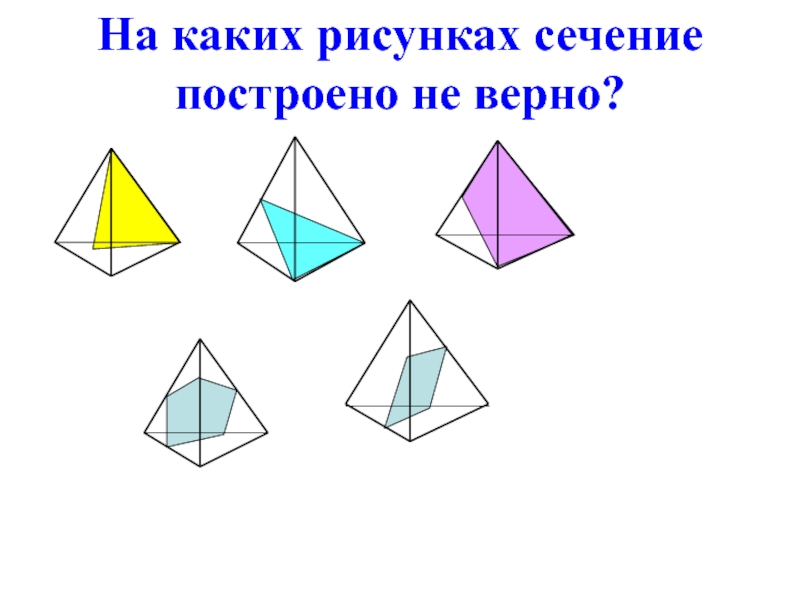
- 19. На каких рисунках сечение построено не верно?
- 20. Самостоятельная работа 1 вариант1.Сделайте рисунок четырехугольной пирамиды,
- 21. Домашняя работа §2; п.32;33Задача №239
- 22. Спасибо за урок!!!В истории черпаем мы мудрость,
ОпределениеПирамида – многогранник, составленный из n - угольника А1А2…Аn и n треугольниковВысота – перпендикуляр, проведенный из вершины пирамиды к плоскости основанияБоковые ребра
Слайд 1
ПИРАМИДА
Преподаватель: Косян Анаит Георгиевна
Богучар -2016 год
ПРЕДМЕТ «МАТЕМАТИКА»
ПРЕЗЕНТАЦИЯ ОТКРЫТОГО УРОКА
ГБПОУ ВО
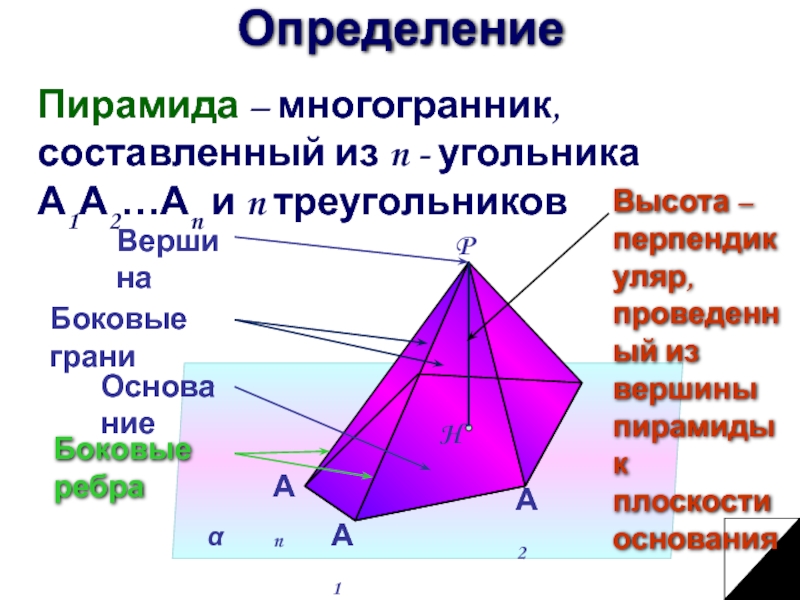
Слайд 2Определение
Пирамида – многогранник, составленный из n - угольника А1А2…Аn и n
треугольников
Высота – перпендикуляр, проведенный из вершины пирамиды к плоскости основания
Боковые ребра
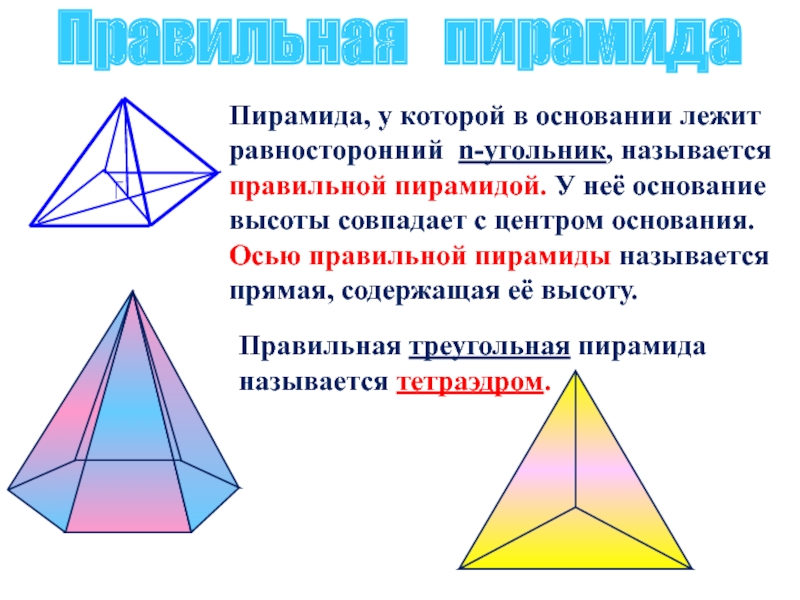
Слайд 5Правильная пирамида
Пирамида, у которой в основании лежит равносторонний n-угольник, называется
правильной пирамидой. У неё основание высоты совпадает с центром основания.
Осью правильной пирамиды называется прямая, содержащая её высоту.
Правильная треугольная пирамида называется тетраэдром.
Слайд 6Все боковые ребра правильной пирамиды равны, а боковые грани являются равными
равнобедренными треугольниками.
Слайд 7Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины.
Апофемы
Все апофемы правильной пирамиды равны друг другу
Слайд 8Теорема о площади боковой
поверхности правильной пирамиды
Площадь боковой поверхности правильной пирамиды
равна половине произведения периметра основания на апофему
Док – во:
Sбок = (½ad + ½ad + ½ad) =
= ½d(a + a + a)= ½dP
Sбок = ½dP
Слайд 11Решение задач
А
В
С
D
S
О
230 м
№1.В основании пирамиды Хеопса – квадрат со стороной
230м, высота пирамиды 138 м. Найти боковое ребро самой высокой египетской пирамиды.
Решение:
1. AC ∩ ВD = О
2. Δ АОD – п\у, р\б
по т. Пифагора
АD2 = DО2+ОА2
2ОD2= 2302 = 52900
ОD2 = 26450
3. Пирамида правильная ⇒
SО ⊥ (АВС)
4. Δ SОD – п\у
по т. Пифагора DS2 = DО2+ОS2 = 26450 + 1382=
= 26450 +19044 = 45494
DS ≈ 213 м
Ответ: 213 м.
D
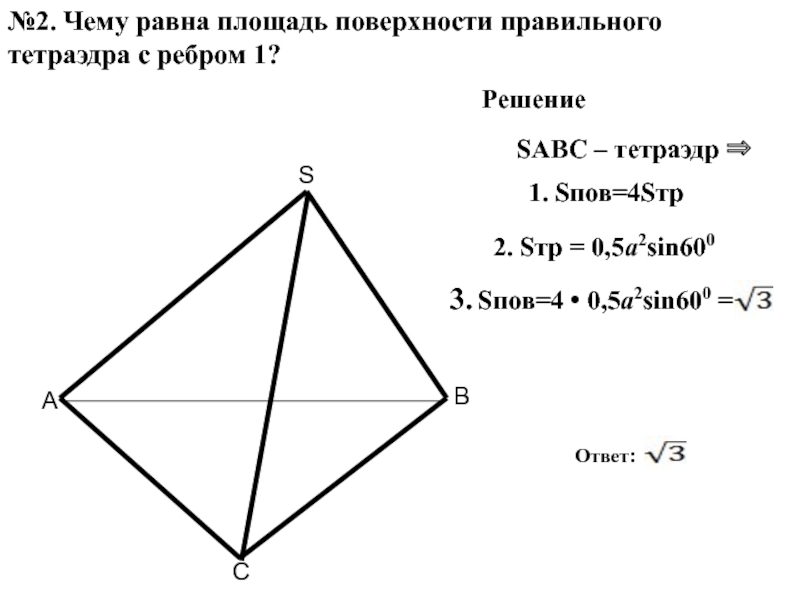
Слайд 12№2. Чему равна площадь поверхности правильного тетраэдра с ребром 1?
A
C
B
S
Решение
SABC –
тетраэдр ⇒
1. Sпов=4Sтр
3. Sпов=4 • 0,5а2sin600 =
Ответ:
2. Sтр = 0,5а2sin600
Слайд 133. (устно) Боковое ребро правильной пирамиды вдвое больше ее высоты. Определите
угол наклона бокового ребра к плоскости основания.
А
D
С
В
S
О
Решение:
1. AC ∩ ВD = О
2. Пирамида правильная⇒
SО ⊥ (АВС) ⇒ Δ SОD –
прямоугольный Δ
3. SD = 2• SO
4. ∠ D = 300
Ответ: 300.
Слайд 14Немного истории
Первым из наших современников, кто установил ряд
необычных явлений, связанных с пирамидой, был французский ученый Антуан Бови. Исследуя пирамиду Хеопса в 30-х годах двадцатого столетия, он обнаружил, что тела мелких животных, случайно попавших в царскую комнату, мумифицировались. Причину этого Бови объяснил для себя формой пирамиды и, как оказалось не ошибся. Его труды легли в основу современных исследований, в результате которых за последние 20 лет появилось множество книг и публикаций, подтверждающих, что энергия пирамид может иметь прикладное значение.
Слайд 16Построение сечения пирамиды
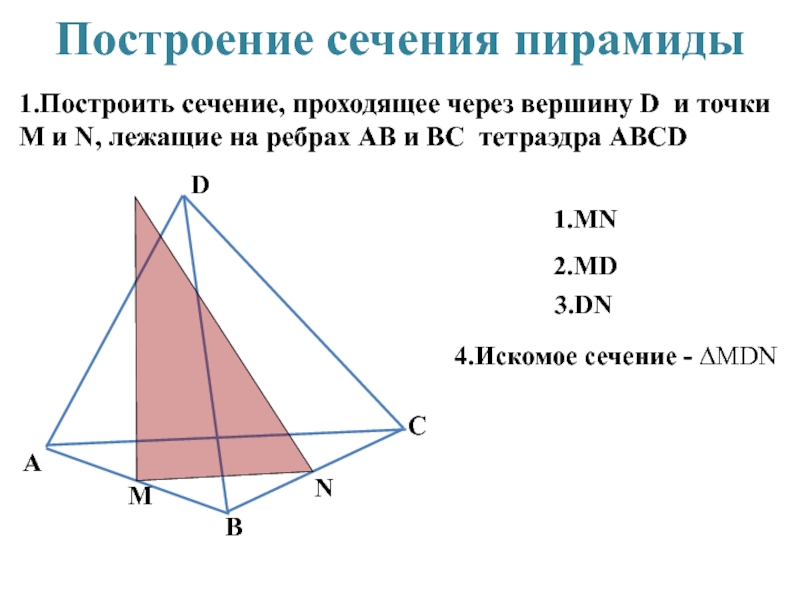
1.Построить сечение, проходящее через вершину D и точки М
и N, лежащие на ребрах AB и BC тетраэдра ABCD
M
N
1.MN
2.MD
3.DN
4.Искомое сечение - ∆MDN
B
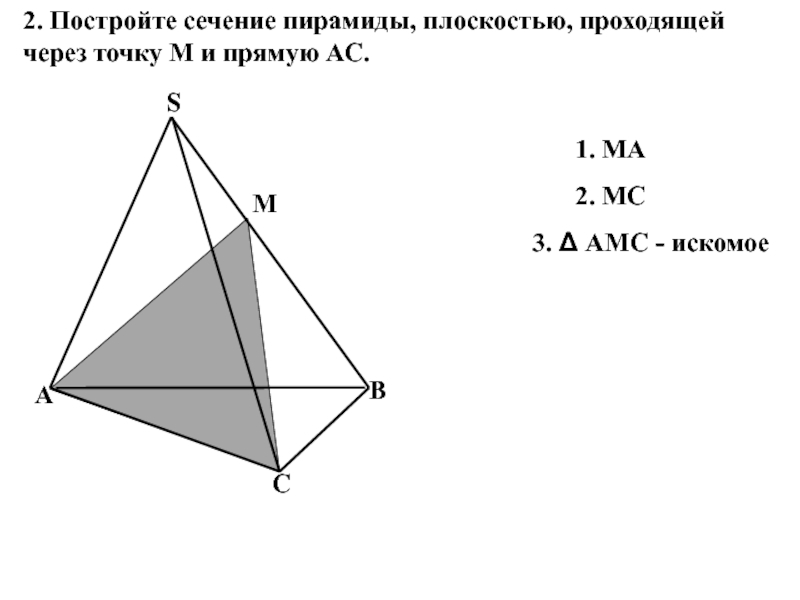
Слайд 172. Постройте сечение пирамиды, плоскостью, проходящей через точку М и прямую
АС.
S
А
С
В
М
1. МА
2. МС
3. Δ АМС - искомое
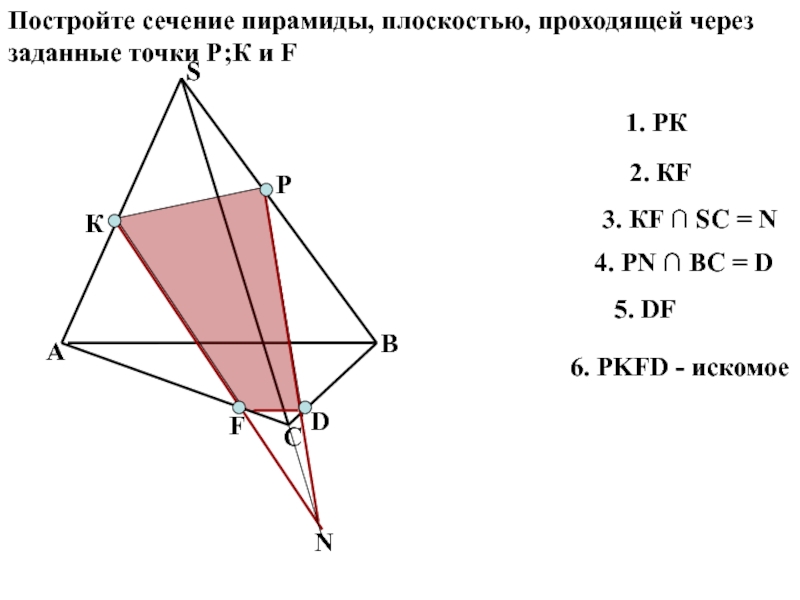
Слайд 18Постройте сечение пирамиды, плоскостью, проходящей через заданные точки Р;К и F
1.
РК
2. КF
3. КF ∩ SС = N
4. РN ∩ ВС = D
5. DF
6. PKFD - искомое
А
S
В
С
F
D
К
Р
N
Слайд 20Самостоятельная работа
1 вариант
1.Сделайте рисунок четырехугольной пирамиды, обозначьте ее и запишите:
вершину, боковые ребра, основание, боковые грани.
2.Закончите предложения:
а) высотой пирамиды называется …;
б) пирамида называется правильной, если …;
3.Найти площадь поверхности правильной треугольной пирамиды, если сторона её основания 2 см, а высота боковой грани 6см.
2 вариант
1.Сделайте рисунок треугольной пирамиды, обозначьте ее и запишите: вершину, боковые ребра, основание, боковые грани.
2.Закончите предложения:
а) апофемой правильной пирамиды называется …;
б) боковой поверхностью пирамиды называется …;
3.Найти площадь поверхности правильной четырехугольной пирамиды, если сторона её основания 4 м, а высота бок. грани 7м.
2.Закончите предложения:
а) высотой пирамиды называется …;
б) пирамида называется правильной, если …;
3.Найти площадь поверхности правильной треугольной пирамиды, если сторона её основания 2 см, а высота боковой грани 6см.
2 вариант
1.Сделайте рисунок треугольной пирамиды, обозначьте ее и запишите: вершину, боковые ребра, основание, боковые грани.
2.Закончите предложения:
а) апофемой правильной пирамиды называется …;
б) боковой поверхностью пирамиды называется …;
3.Найти площадь поверхности правильной четырехугольной пирамиды, если сторона её основания 4 м, а высота бок. грани 7м.
Слайд 22Спасибо за урок!!!
В истории черпаем мы мудрость,
в поэзии – остроумие,
в
математике-проницательность.
Бэкон Френсис (Англ. философ; 16 век)
Бэкон Френсис (Англ. философ; 16 век)
