- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике НА ТЕМУ:ДВИЖЕНИЕ.
Содержание
- 1. ПРЕЗЕНТАЦИЯ по математике НА ТЕМУ:ДВИЖЕНИЕ.
- 2. Центральная симметрия Две точки А и
- 3. Фигура называется симметричной относительно точки О если
- 4. Осевая симметрия Две точки
- 5. Фигура называется симметричной относительно прямой а, если
- 6. Прямоугольник и ромб, не являющиеся квадратами имеют
- 7. Имеются фигуры, у которых нет ни одной
- 8. Зеркальная симметрияЗеркальная симметрия - это отображение пространства
- 9. Зеркально симметричные объектыОсевая симметрияЗеркальная симметрияЦентральная симметрия
- 10. Напишем на листе бумаги заглавными печатными буквами
- 11. Слайд 11
- 12. Слайд 12
- 13. Зеркало не подействовало на слово " КОФЕ
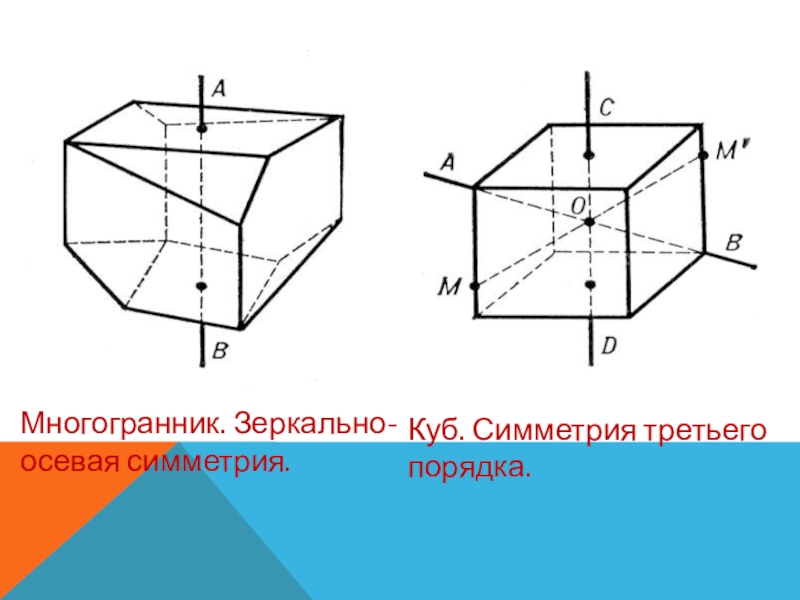
- 14. Многогранник. Зеркально-осевая симметрия.Куб. Симметрия третьего порядка.
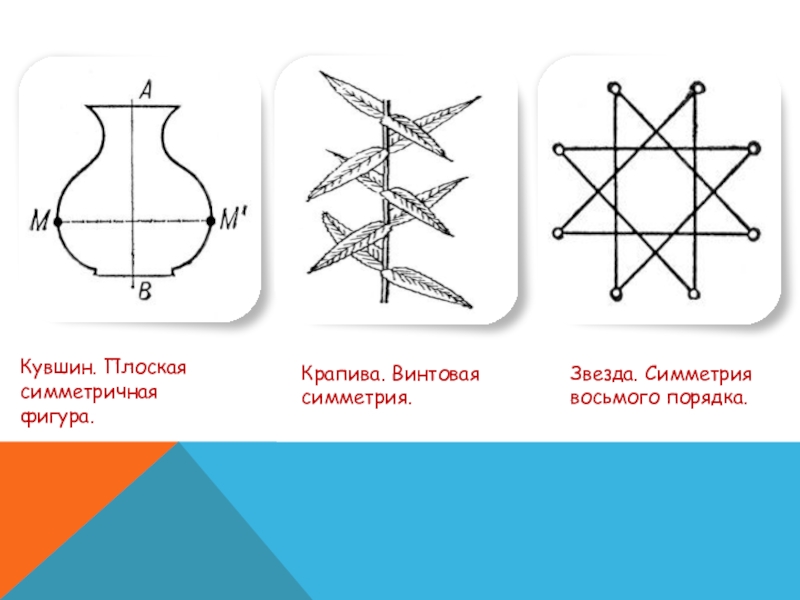
- 15. Кувшин. Плоская симметричная фигура. Крапива. Винтовая симметрия. Звезда. Симметрия восьмого порядка.
- 16. Зеркальная симметрия в природе
- 17. Параллельный перенос
- 18. Поворот (вращение) — движение, при котором по
- 19. Параллельный перенос ― частный случай движения, при
- 20. ОСЕВАЯ СИММЕТРИЯЦЕНТРАЛЬНАЯ СИММЕТРИЯПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСПОВОРОТДВИЖЕНИЕ
- 21. Свойства движения:При движении прямая переходит в прямую,
- 22. Следствие:При движении фигура переходит в равную ей фигуру!!!
- 23. ГОМОТЕТИЯ.Гомотетия – одно из важнейших преобразований подобия.При гомотетии сохраняются только углы!!!
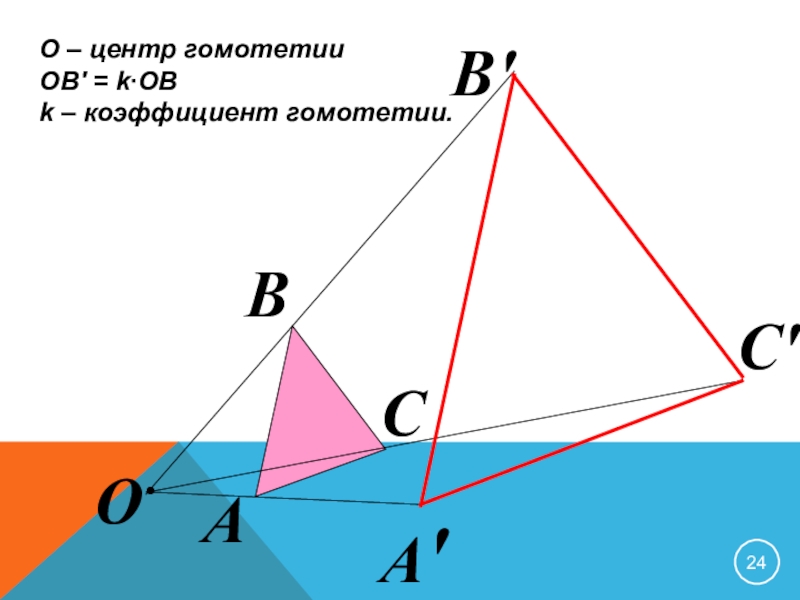
- 24. О – центр гомотетииОВ′ = k∙ОВk – коэффициент гомотетии.ОАА′ВВ′СС′
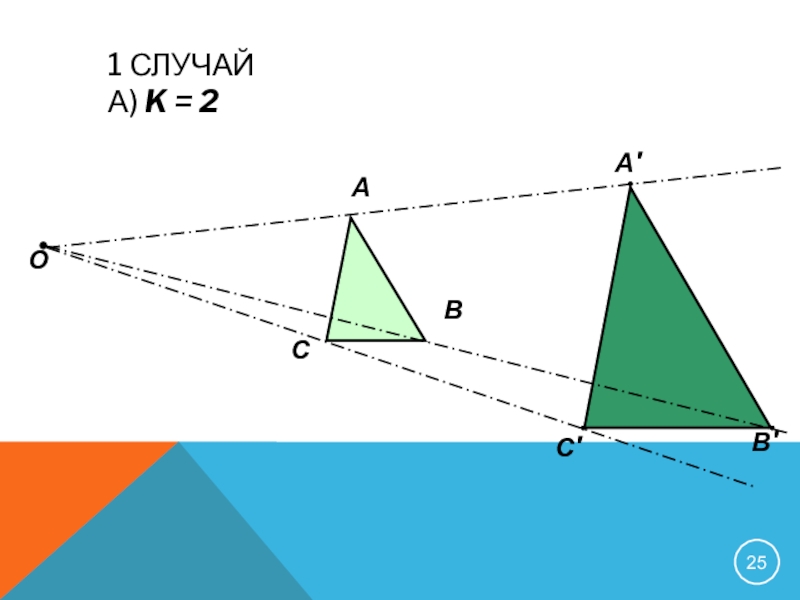
- 25. 1 случай а) k = 2О
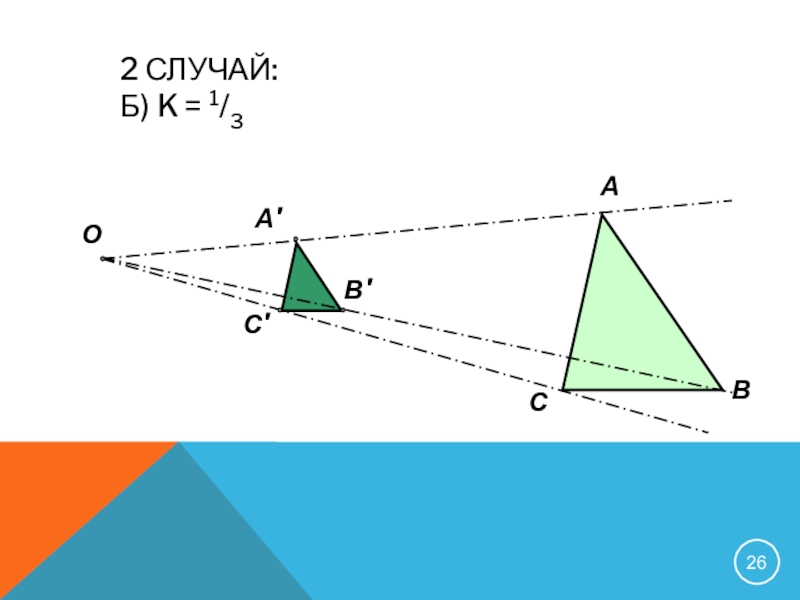
- 26. 2 случай: б) k = 1/3 АВСОА′В′С′
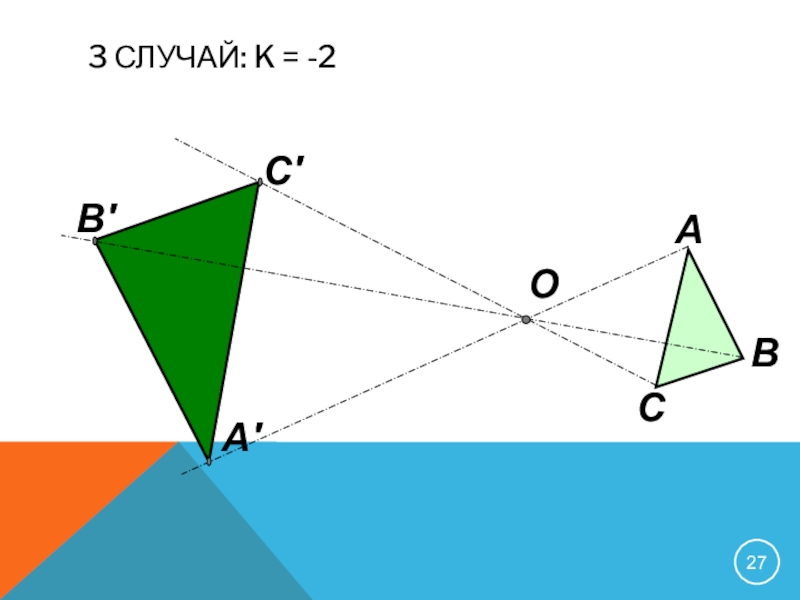
- 27. 3 случай: k = -2ОАВСА′В′С′
- 28. Конец!
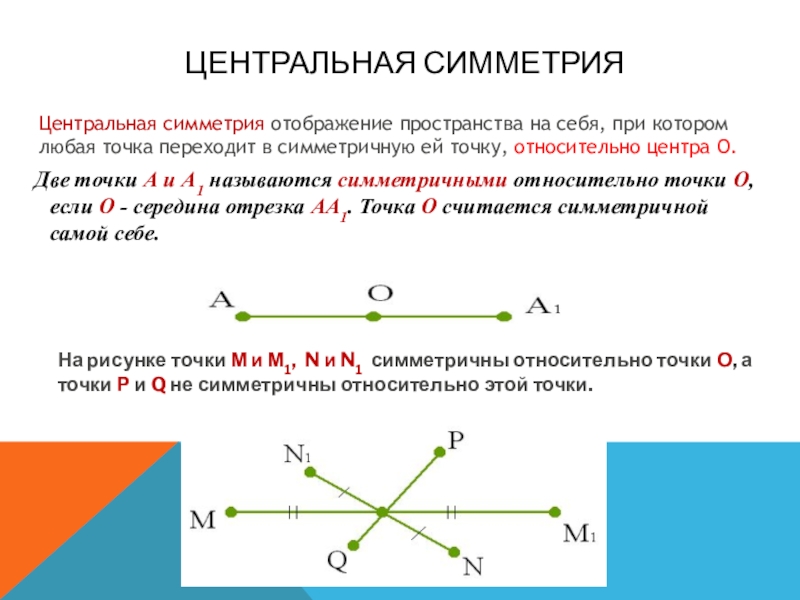
Слайд 2Центральная симметрия
Две точки А и А1 называются симметричными относительно
На рисунке точки М и М1, N и N1 симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки.
Центральная симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно центра О.
Слайд 3Фигура называется симметричной относительно точки О
если для каждой точки фигуры
Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм.
Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма точка пересечения его диагоналей.
Слайд 4Осевая симметрия
Две точки А и А1 называются
Каждая точка прямой а считается симметричной самой себе.
Осевая симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно оси а.
Слайд 5Фигура называется симметричной относительно прямой а, если для каждой точки фигуры
Говорят также, что фигура обладает осевой симметрией.
У неразвёрнутого угла одна ось симметрии - прямая, на которой расположена биссектриса угла.
Равнобедренный(но не равносторонний) треугольник имеет также одну ось симметрии, а равносторонний треугольник - три основные симметрии.
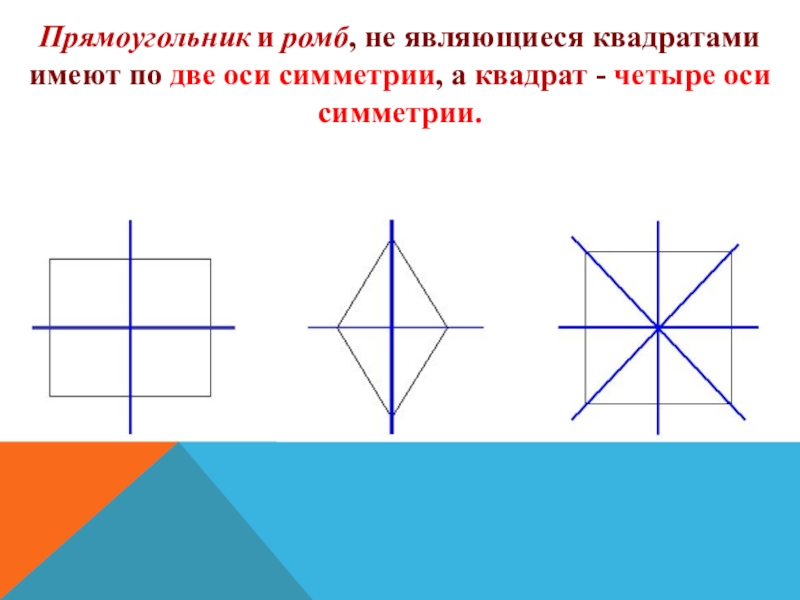
Слайд 6Прямоугольник и ромб, не являющиеся квадратами имеют по две оси симметрии,
Слайд 7
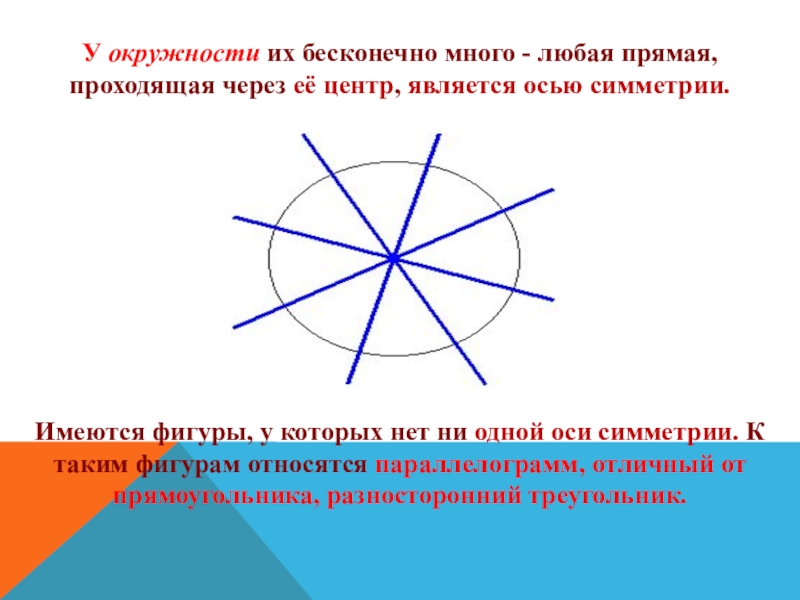
Имеются фигуры, у которых нет ни одной оси симметрии. К таким
У окружности их бесконечно много - любая прямая, проходящая через её центр, является осью симметрии.
Слайд 8Зеркальная симметрия
Зеркальная симметрия - это отображение пространства на себя, при котором
Слайд 10Напишем на листе бумаги заглавными печатными буквами два слова "КОФЕ" и
Слайд 13Зеркало не подействовало на слово " КОФЕ " , тогда как
Слайд 15Кувшин. Плоская
симметричная фигура.
Крапива. Винтовая
симметрия.
Звезда. Симметрия
восьмого порядка.
Слайд 18Поворот (вращение) — движение, при котором по крайней мере одна точка
А вот параллельный перенос – это движение, когда все точки плоскости
переносятся на одно и то же расстояние в одном и том же направлении
Слайд 19Параллельный перенос ― частный случай движения, при котором все точки пространства
Параллельный перенос перемещает каждую точку фигуры или пространства на одно и то же расстояние в одном и том же направлении.
Параллельный перенос
Слайд 21Свойства движения:
При движении прямая переходит в прямую, луч – в луч,
Сохраняются расстояния между точками.
Сохраняются углы между лучами.