- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему:Декартова система координат
Содержание
- 1. Презентация по математике на тему:Декартова система координат
- 2. Цели урока:Образовательные: рассмотреть понятие системы координат и
- 3. Развивающие: способствовать развитию пространственного воображения учащихся, способствовать выработке решения задач и развития логического мышления учащихся.
- 4. Воспитательные: воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
- 5. План урока:1. Организационный момент;2. Введение;3. Сообщение целей урока;4. Актуализация;5. Изучение нового материала;6. Закрепление: решение задач.
- 6. Декарт был крупнейшим философом и математиком своего
- 7. ОПРЕДЕЛЕНИЕПрямоугольная система координат на плоскости образуется двумя
- 8. Если в качестве координатных осей берутся
- 9. В элементарной математике чаще всего рассматривается двухмерная
- 10. Слайд 10
- 11. Три плоскости, проходящие через
- 12. В прямоугольной системе координат каждой
- 13. Координатные оси делят координатную плоскость на четыре
- 14. ФормулыРасстояние между двумя точками: Координаты середины отрезка BC:
- 15. Формула для нахождения координаты середины отрезка AB
- 16. Решение задачЗадача 1: На плоскости заданы координаты
- 17. Таким образом, середина отрезка AB имеет координаты:
- 18. Задача 2: Найдите длину медианы АМ в
- 19. Теперь воспользуемся формулой для вычисления расстояния между точками A и M:Ответ:
- 20. Задача 3: В прямоугольной системе координат трехмерного
- 21. Итак, точка А имеет координаты (7;3;-8)
Цели урока:Образовательные: рассмотреть понятие системы координат и координаты точки в пространстве, вывести формулу расстояния в координатах, вывести формулу координат середины отрезка.
Слайд 2Цели урока:
Образовательные: рассмотреть понятие системы координат и координаты точки в пространстве,
вывести формулу расстояния в координатах, вывести формулу координат середины отрезка.
Слайд 3Развивающие: способствовать развитию пространственного воображения учащихся, способствовать выработке решения задач и
развития логического мышления учащихся.
Слайд 4Воспитательные: воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Слайд 5План урока:
1. Организационный момент;
2. Введение;
3. Сообщение целей урока;
4. Актуализация;
5. Изучение нового
материала;
6. Закрепление: решение задач.
6. Закрепление: решение задач.
Слайд 6Декарт был крупнейшим философом и математиком своего времени. В основе его
философии лежал материализм. Самым известным трудом Декарта является его “Геометрия”. Декарт ввел систему координат, которой пользуются все и в настоящее время. Он установил соответствие между числами и отрезками прямой и таким образом ввел алгебраический метод в геометрию.
Р. Декарт — французский ученый (1596— 1650)
Слайд 7ОПРЕДЕЛЕНИЕ
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат
OX и OY. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для обеих осей.
Слайд 8 Если в качестве координатных осей берутся прямые, перпендикулярные друг другу,
то система координат называется
Прямоугольной
(ортогональльной)
Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется
ортонормированной (декартовой)
Слайд 9В элементарной математике чаще всего рассматривается двухмерная или трехмерная декартова система
координат
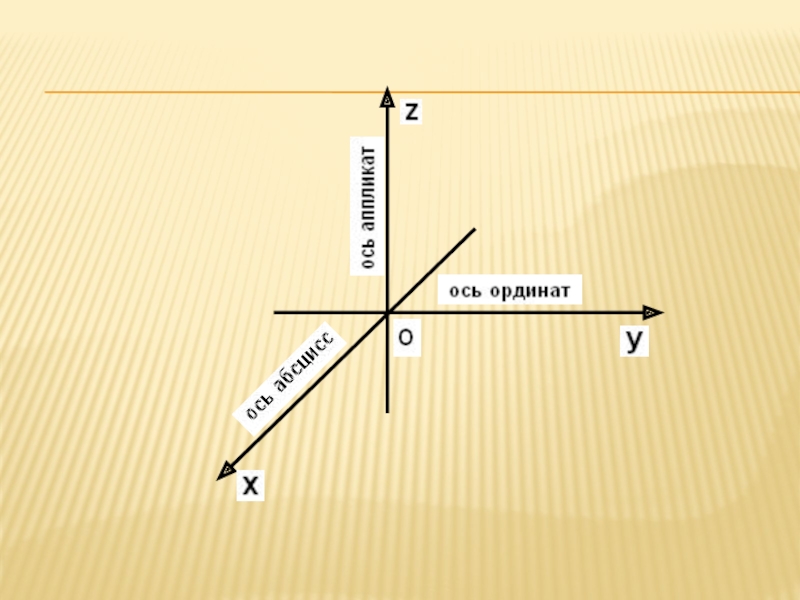
Координаты обычно обозначаются латинскими буквами x, y, z и называются, соответственно, абсциссой, ординатой и аппликатой. Координатная ось OX называется осью абсцисс, ось OY – осью ординат, ось OZ – осью аппликат. Положительные направления отсчета по каждой из осей обозначаются стрелками.
Слайд 11 Три плоскости, проходящие через оси координат Ох и
Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями: Оху, Оуz, Оzх.
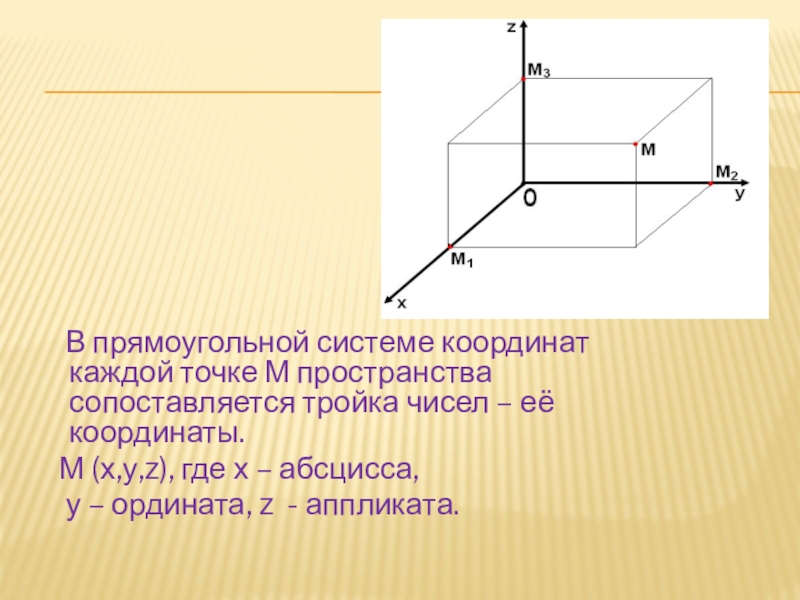
Слайд 12 В прямоугольной системе координат каждой точке М пространства сопоставляется
тройка чисел – её координаты.
М (х,у,z), где х – абсцисса,
у – ордината, z - аппликата.
М (х,у,z), где х – абсцисса,
у – ордината, z - аппликата.
Слайд 13Координатные оси делят координатную плоскость на четыре квадранта (четверти). Точки, лежащие
на осях координат, не принадлежат ни одному квадранту.
В двухмерной системе координат все точки, лежащие над (под) осью OX, образуют верхнюю (нижнюю) координатную полуплоскость. Все точки, лежащие правее (левее) оси OY образуют правую (левую) координатную полуплоскость.
Слайд 16Решение задач
Задача 1: На плоскости заданы координаты двух точек
A(-7;3) и B(2;4). Найдите координаты середины отрезка AB.
Решение:
Пусть точка C-середина отрезка AB. Её координаты равны полусуммам соответствующих координат точек A и B
Решение:
Пусть точка C-середина отрезка AB. Её координаты равны полусуммам соответствующих координат точек A и B
Слайд 18Задача 2: Найдите длину медианы АМ в треугольнике АВС, если известны
координаты его вершин A(-1;0), B(3;2), C(9;-8).
Решение: Так как АМ – медиана, то точка М является серединой стороны ВС. Найдем координаты середины этого отрезка по известным координатам его концов:
Таким образом M(6;-3)
Решение: Так как АМ – медиана, то точка М является серединой стороны ВС. Найдем координаты середины этого отрезка по известным координатам его концов:
Таким образом M(6;-3)
Слайд 20Задача 3: В прямоугольной системе координат трехмерного пространства дан параллелепипед
.Известно,что ; M(4;2;-4)-середина диагонали . Найдите координаты точки А.
Решение: Диагонали параллелограмма пересекаются в одной точке, и эта точка является серединой каждой из этих диагоналей. Таким образом, мы можем утверждать, что точка М является серединой отрезка
Решение: Диагонали параллелограмма пересекаются в одной точке, и эта точка является серединой каждой из этих диагоналей. Таким образом, мы можем утверждать, что точка М является серединой отрезка
Из формул для нахождения координат середины отрезка имеем:
