- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Замечательные кривые
Содержание
- 1. Презентация по математике на тему Замечательные кривые
- 2. Актуальность темы заключается в демонстрации применения математических
- 3. Конические сечения – замечательные кривые
- 4. Сечением конуса плоскостью параллельно окружности основания является
- 5. Если плоскость сечения будет параллельна только одной
- 6. Замечательные кривые 2 порядка в координатной плоскости
- 7. Общее уравнение кривой 2 порядкаОпределение: Кривой второго
- 8. ОкружностьОпределение: Окружность - замкнутая плоская кривая, все
- 9. Эллипс (от др. - греч. недостаток) Определение:
- 10. Гипербола (греч. hyperbole) - плоская
- 11. Каноническое уравнение гиперболы имеет вид:
- 12. Парабола
- 13. Некоторые другие замечательные кривые
- 14. Спираль АрхимедаПусть по радиусу равномерно вращающегося диска
- 15. СинусоидаСинусоида – волнообразная плоская кривая, которая является
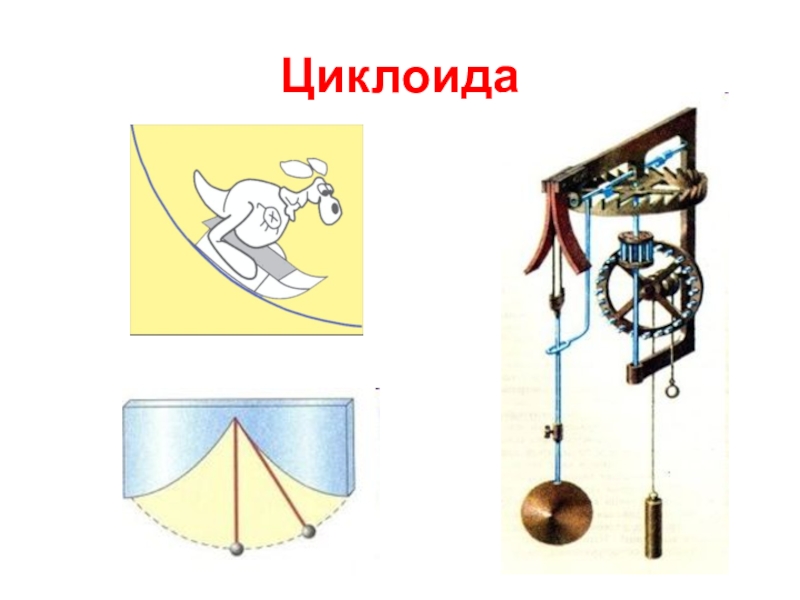
- 16. Циклоида Представьте, что по прямой линии без
- 17. Гипоциклоиды Все кривые, которые вычерчивает точка на
- 18. КАРДИОИДА и УЛИТКА ПАСКАЛЯ (греческое слово
- 19. Построение замечательных кривых с помощью школьных инструментов
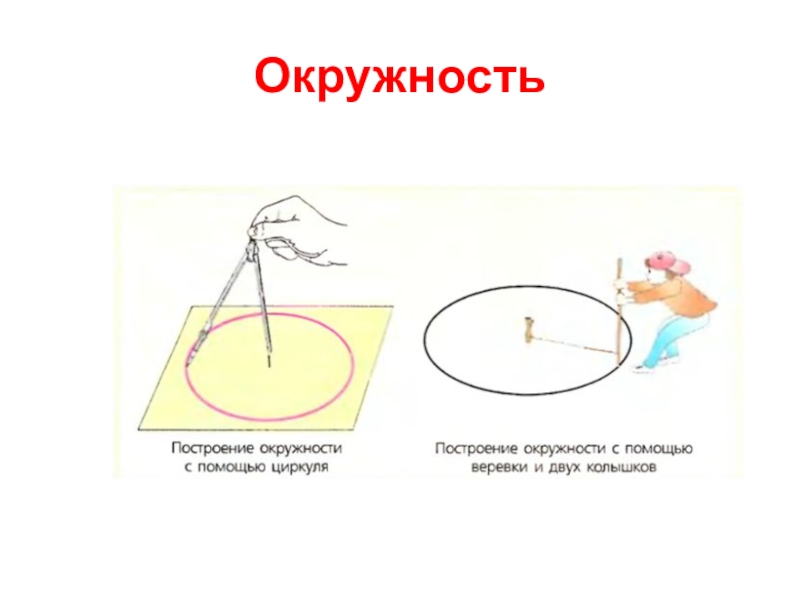
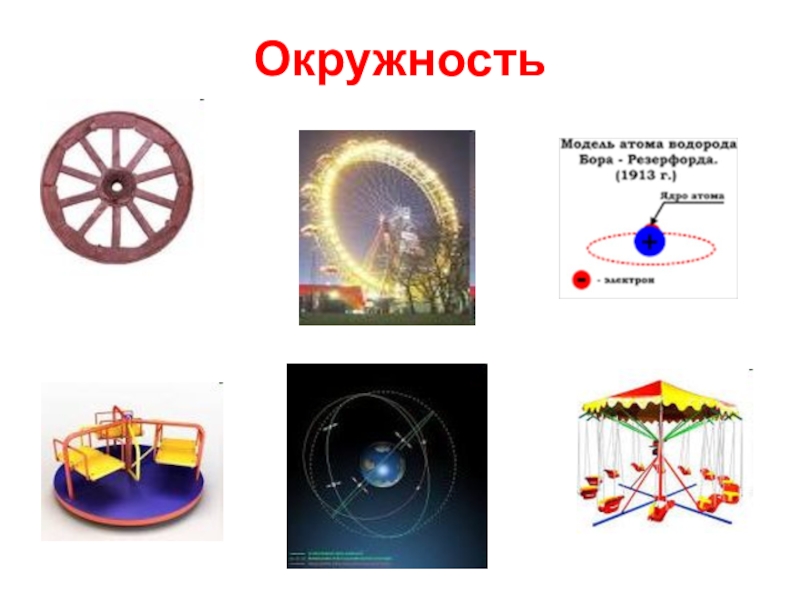
- 20. Окружность
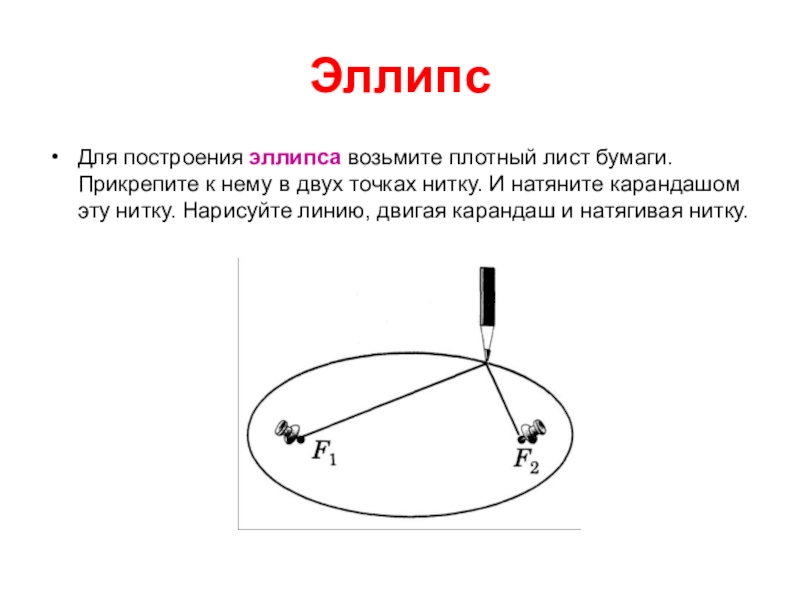
- 21. Эллипс Для построения эллипса возьмите плотный лист
- 22. Слайд 22
- 23. Гипербола Используя определение гиперболы, нетрудно изготовить простейший
- 24. Слайд 24
- 25. Парабола Для построения параболы на листе бумаги
- 26. Слайд 26
- 27. Синусоида Сделайте из плотной бумаги, скатав её
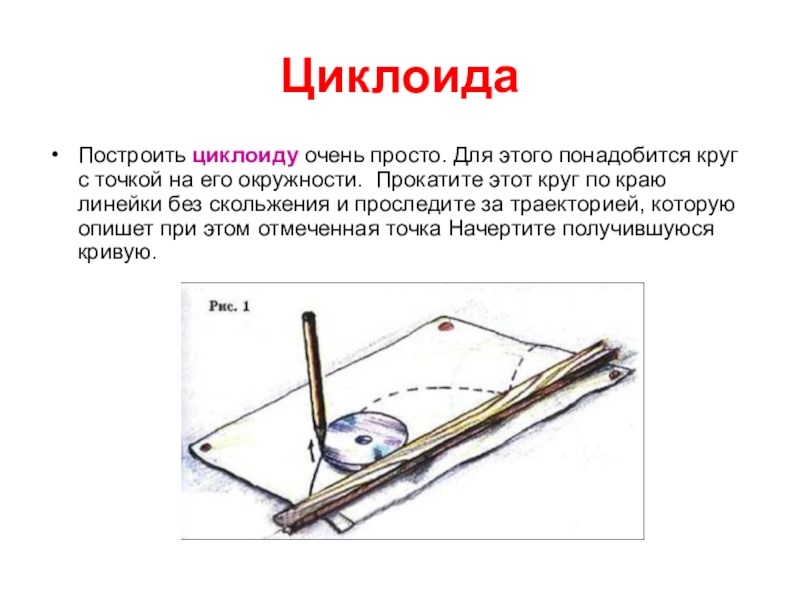
- 28. Циклоида Построить циклоиду очень просто. Для этого
- 29. ГипоциклоидаДля получения гипоциклоиды возьмите кусок толстого картона
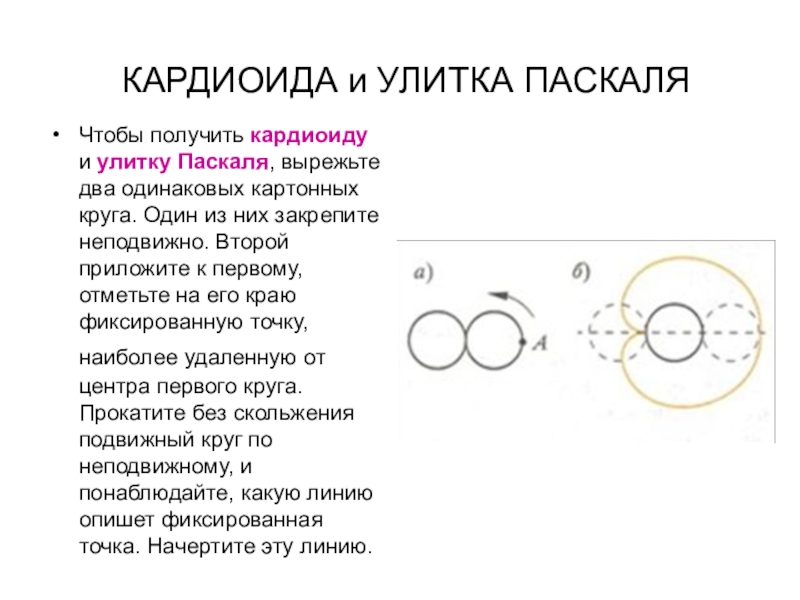
- 30. КАРДИОИДА и УЛИТКА ПАСКАЛЯ Чтобы получить
- 31. Свойства замечательных кривых и их применение
- 32. Окружность
- 33. Эллипс
- 34. Гипербола
- 35. Парабола
- 36. Спираль Архимеда
- 37. Циклоида
- 38. Синусоида
- 39. Кардиоида и улитка Паскаля
- 40. Спасибо за внимание!
Слайд 1Замечательные кривые
Фоменко Марина Юрьевна,
учитель математики МБОУ «Сакская СШ № 4
Ф. И. Сенченко», г. Саки, Республика Крым
Слайд 2
Актуальность темы заключается в демонстрации применения математических знаний в практической деятельности
Гипотеза: Использование данного материала на уроках математики расширяет кругозор учащихся по кривым, изучаемым в школьной программе – окружность, парабола и гипербола, и показывает их практическое применение в жизни.
Цель данной работы: изучение теории и практики замечательных кривых.
Задачи: Отобрать, изучить, обобщить и систематизировать материал по теме, создать наглядные пособия в виде презентации и приборов для построения кривых.
Практическая значимость работы: Считаю, что моя работа пригодится учителям доступно и красочно продемонстрировать учащимся практическое применение свойств замечательных кривых, научить строить кривые при помощи обычных школьных инструментов.
Знакомство с кривыми, изучение их свойств позволит расширить геометрические представления, углубить знания, повысить интерес к геометрии; создаст содержательную основу для дальнейшего изучения математики, физики и других наук.
Слайд 4
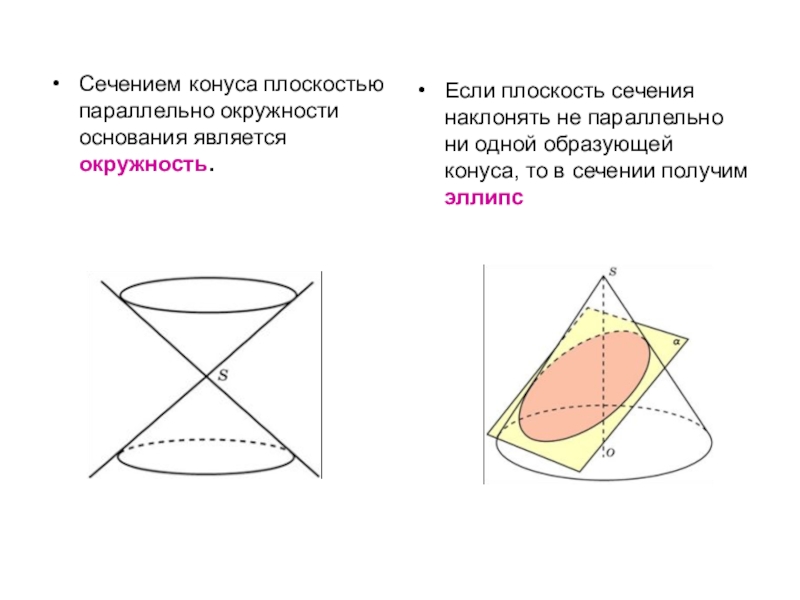
Сечением конуса плоскостью параллельно окружности основания является окружность.
Если плоскость сечения
Слайд 5
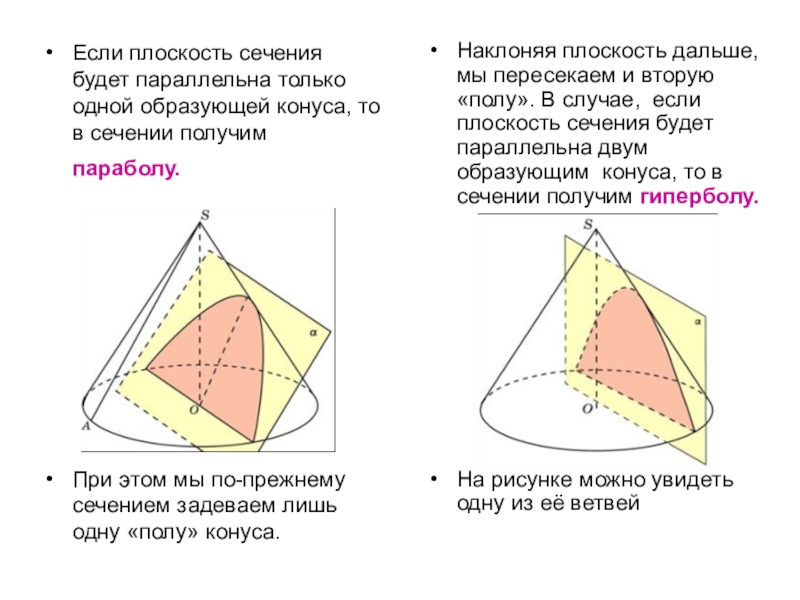
Если плоскость сечения будет параллельна только одной образующей конуса, то в
При этом мы по-прежнему сечением задеваем лишь одну «полу» конуса.
Наклоняя плоскость дальше, мы пересекаем и вторую «полу». В случае, если плоскость сечения будет параллельна двум образующим конуса, то в сечении получим гиперболу.
На рисунке можно увидеть одну из её ветвей
Слайд 7Общее уравнение кривой 2 порядка
Определение: Кривой второго порядка называется множество точек
где коэффициенты А, 2В, С, 2D, 2E и F - любые числа и, кроме того, числа А, В и С не равны нулю одновременно, т.е. .
Уравнения окружности, эллипса, гиперболы и параболы являются частными случаями данного уравнения
Слайд 8Окружность
Определение: Окружность - замкнутая плоская кривая, все точки которой одинаково удалены
Окружность с центром в точке С(а;b) и радиусом R имеет уравнение в прямоугольных координатах:
Слайд 9Эллипс (от др. - греч. недостаток)
Определение:
Эллипсом называется геометрическое место
F1М и F2М - фокальные радиусы точки М.
Для любой точки М эллипса имеем: F1M + F2M = const > F1F2
Каноническое уравнение эллипса имеет вид:
Где а и b - длины большой и малой полуосей эллипса.
Слайд 10Гипербола
(греч. hyperbole) - плоская кривая линия
Определение: Гиперболой называется
Требуется, чтобы эта постоянная была меньше расстояния между фокусами.
F1М и F2М - фокальные радиусы точки М.
Для любой точки М гиперболы имеем: F1M - F2M = const = 2а < F1F2
Слайд 11
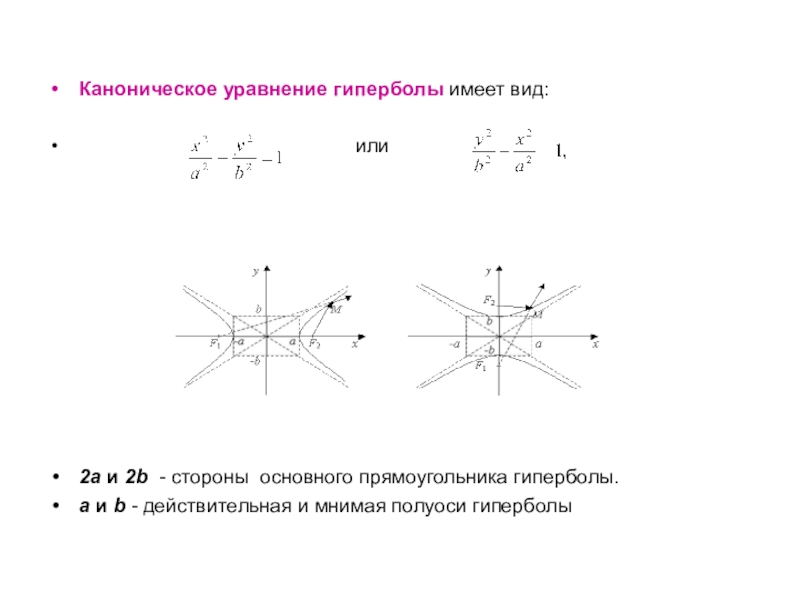
Каноническое уравнение гиперболы имеет вид:
2а и 2b - стороны основного прямоугольника гиперболы.
а и b - действительная и мнимая полуоси гиперболы
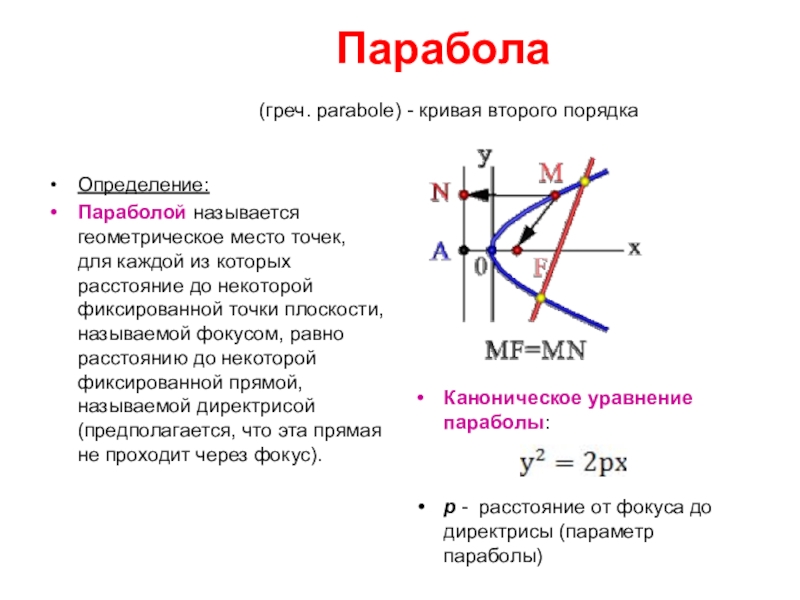
Слайд 12 Парабола (греч. parabole)
Определение:
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой (предполагается, что эта прямая не проходит через фокус).
Каноническое уравнение параболы:
р - расстояние от фокуса до директрисы (параметр параболы)
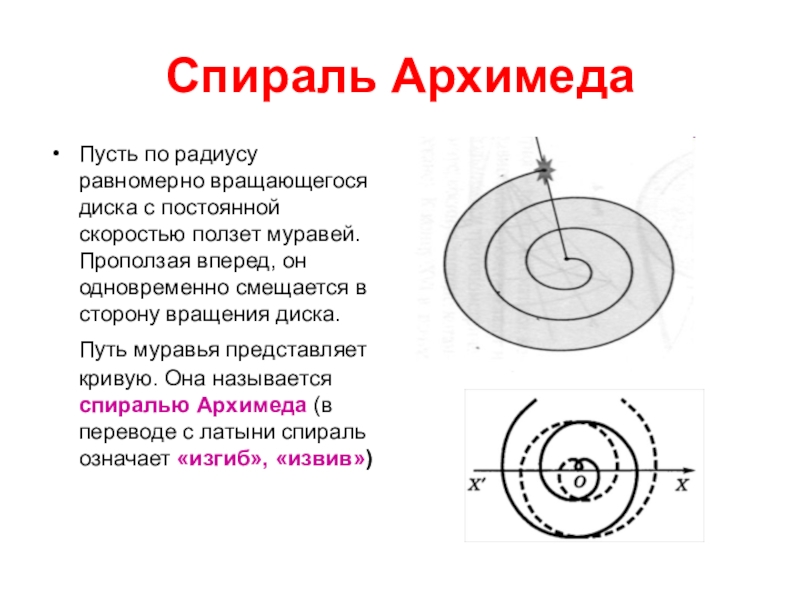
Слайд 14Спираль Архимеда
Пусть по радиусу равномерно вращающегося диска с постоянной скоростью ползет
Слайд 15Синусоида
Синусоида – волнообразная плоская кривая, которая является графиком тригонометрической функции y
Изменение какой-либо величины по закону синуса называется гармоническим колебанием.
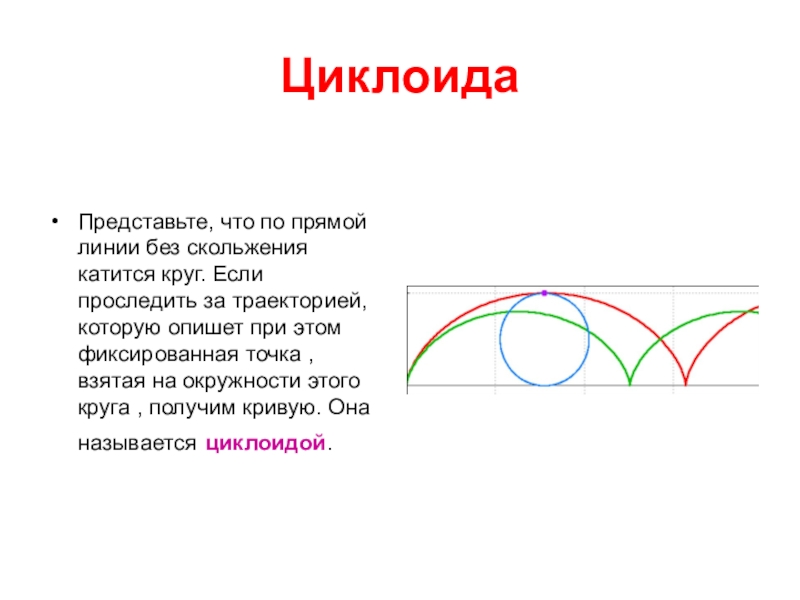
Слайд 16Циклоида
Представьте, что по прямой линии без скольжения катится круг. Если
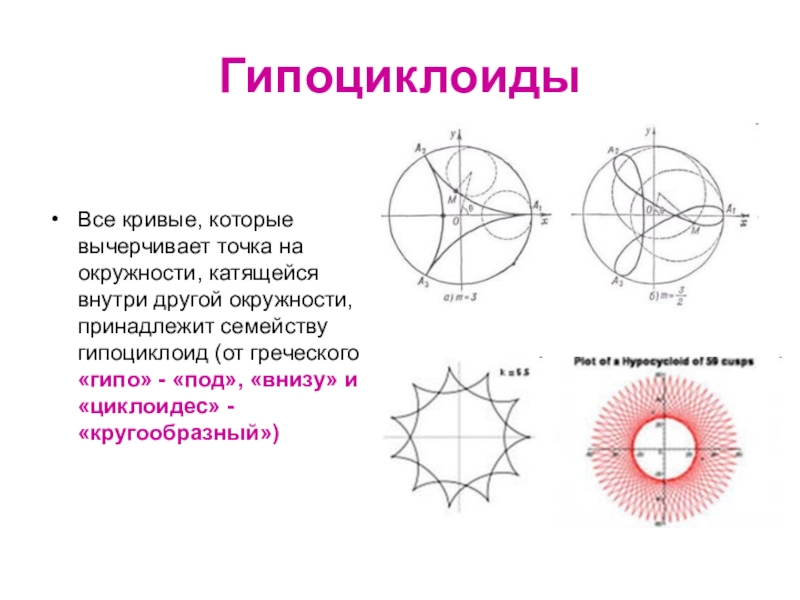
Слайд 17Гипоциклоиды
Все кривые, которые вычерчивает точка на окружности, катящейся внутри другой
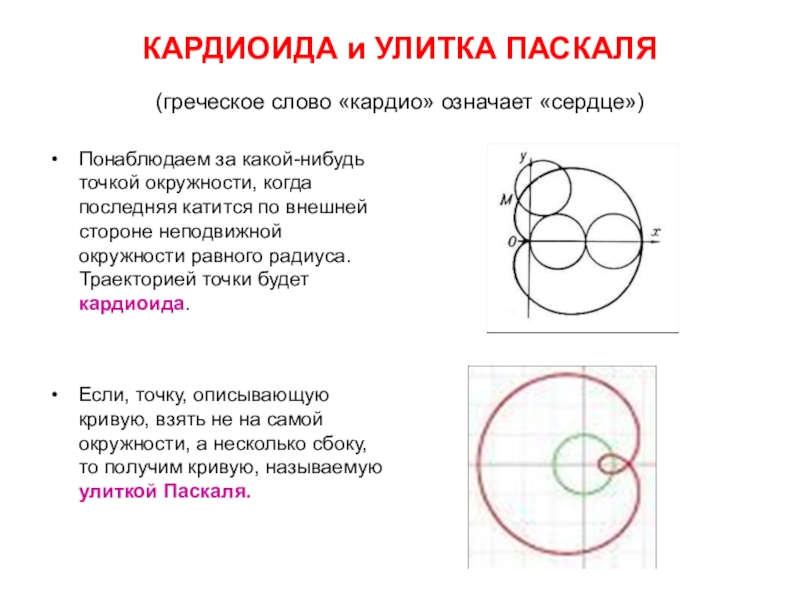
Слайд 18КАРДИОИДА и УЛИТКА ПАСКАЛЯ
(греческое слово «кардио» означает «сердце»)
Понаблюдаем за
Если, точку, описывающую кривую, взять не на самой окружности, а несколько сбоку, то получим кривую, называемую улиткой Паскаля.