- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задача №8 ЕГЭ-2015 по математике, профильный уровень
Содержание
- 1. Презентация по математике на тему Задача №8 ЕГЭ-2015 по математике, профильный уровень
- 2. Задача №8Тип задания по кодификатору требований: Задание
- 3. Задача №8общие точки графика производной и оси
- 4. Решение:Ответ: 59.Задача №8Ответ: 8
- 5. Задача №8Решение: Ответ: 7
- 6. Задача №8Решение: Ответ: 0,5.Решение:
- 7. Задача №8(продолжение решения задачи 5)В нашем случае
- 8. Задача №86. На рисунке изображен график функции
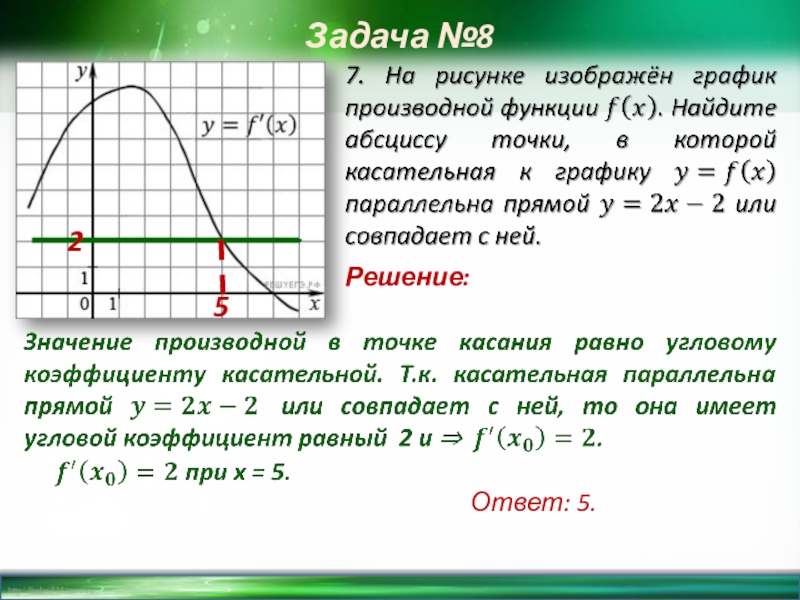
- 9. Задача №8Решение:25Ответ: 5.
- 10. Задача №8Значение производной в точке касания равно
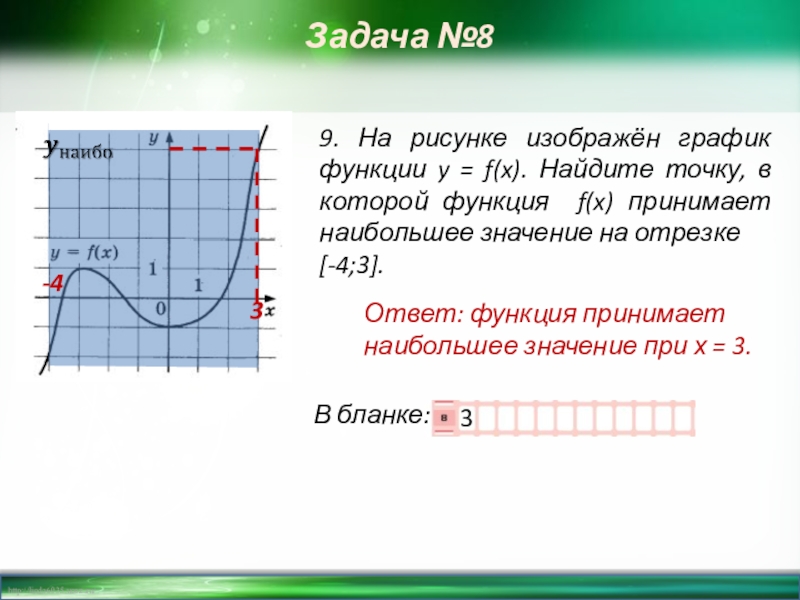
- 11. Задача №89. На рисунке изображён график функции
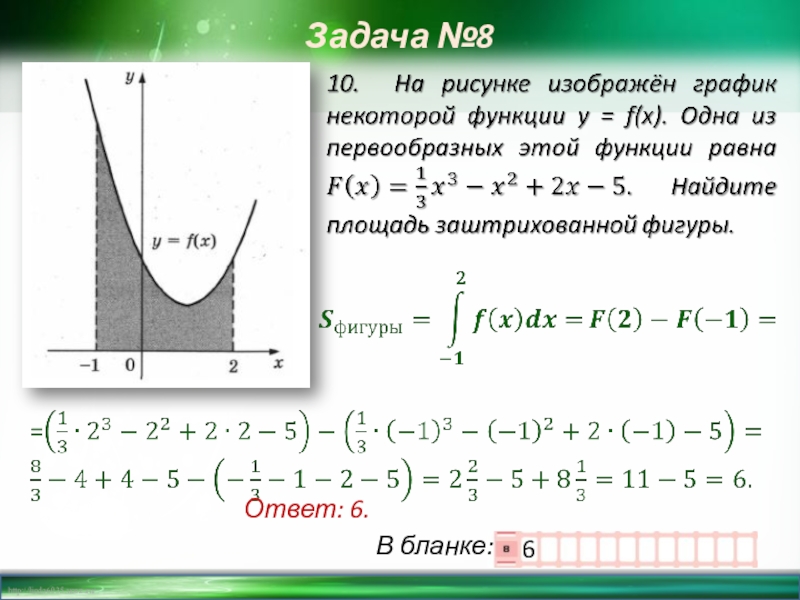
- 12. Задача №8Ответ: 6.
- 13. Задача №811. На рисунке изображён график y
- 14. Задача №8Решение:Выделим интервалы, где производная больше нуля.Ответ: 5.
- 15. Задача №8Решение: Значение производной в точке касания
- 16. Задача №8ACBMNОтвет: 10
- 17. Задача №815. На рисунке изображён график функции
- 18. Задача №816. На рисунке изображён график функции
- 19. Задача №8В каждой точке интервала убывания дифференцируемой на этом интервале функции её производная отрицательнаОтвет: 2
- 20. Ответ: 2Ответ: 3Задача №8
- 21. 20. На рисунке изображён график y=f'(x) — производной функции
- 22. Ответ: -1,2522. На рисунке изображен график производной
- 23. 24. На рисунке изображён график функции y=f(x),
- 24. 25. На рисунке изображён график y=f′(x) производной функции
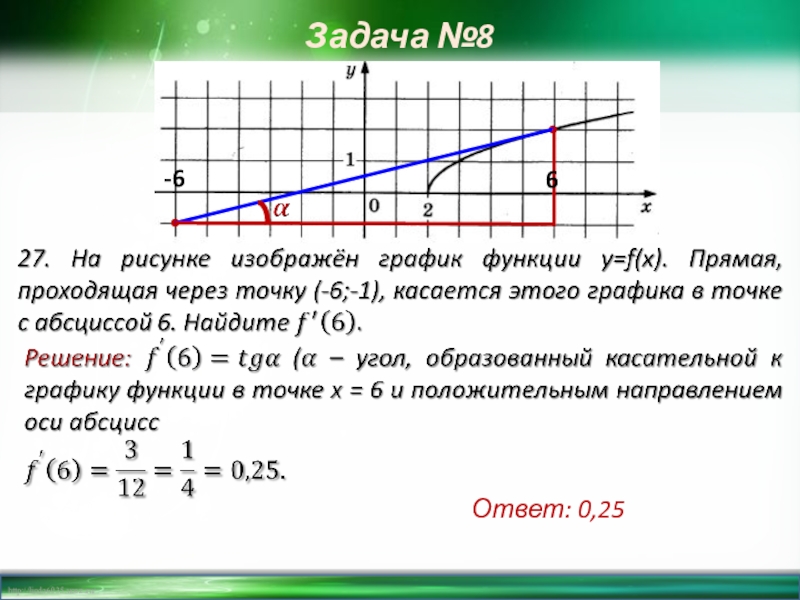
- 25. Задача №8-6••6Ответ: 0,25
- 26. Задача №8Ответ: 0,5
- 27. 29. На рисунке изображен график y=f′(x) — производной
- 28. Задача №830. На рисунке изображен график y=f′(x)
- 29. Задача №8http://reshuege.ru/ЕГЭ 2015. Математика. 30 вариантов типовых
Слайд 1Учитель математики ГБОУ гимназия №1
города Похвистнево Самарской области
Антонова Г.В.
Задача
по математике, профильный уровень
Слайд 2Задача №8
Тип задания по кодификатору требований: Задание на выполнение действий с
Характеристика задания: Задача на чтение графика функции для ответа на вопрос о каком-то из свойств производной этой функции либо на чтение графика производной функции для ответа на вопрос о каком-то из свойств самой функции.
Комментарий: Для решения задачи достаточно знать, что
- в каждой точке интервала возрастания дифференцируемой на этом интервале функции её производная положительна;
- в каждой точке интервала убывания дифференцируемой на этом интервале функции её производная отрицательна;
- в каждой точке экстремума непрерывной функции производная либо равна нулю, либо не существует («угол» на графике функции).
Слайд 3Задача №8
общие точки графика производной и оси абсцисс (т.е. точки, в
либо являются точками максимума, если график производной пересекает ось абсцисс «сверху вниз» (т.е. производная меняет знак с плюса на минус: возрастание функции сменяется убыванием),
либо являются точками минимума, если график производной пересекает ось абсцисс «снизу вверх» (т.е. производная меняет знак с минуса на плюс: убывание функции сменяется возрастанием),
либо не являются точками экстремума (график производной не пересекает ось абсцисс, а лишь касается её: в этом случае не происходит смены знака производной и характер монотонности функции НЕ МЕНЯЕТСЯ).
Обратно, если дан график производной функции, то
на тех интервалах, где он расположен выше оси абсцисс (т.е. производная положительна), функция возрастает;
на тех интервалах, где он расположен ниже оси абсцисс (т.е. производная отрицательна), функция убывает;
Слайд 7Задача №8
(продолжение решения задачи 5)
В нашем случае имеем:
Проверка подстановкой показывает, что
Ответ: -1.
-
Слайд 8Задача №8
6. На рисунке изображен график функции y=f(x). Прямая, проходящая через
Т.к. касательная проходит через начало координат и точку (8;10), проведём её.
8
10
Ответ: 1,25.
Слайд 10Задача №8
Значение производной в точке касания равно угловому коэффициенту касательной. Т.к.
Решение:
•
-3
Ответ: - 3.
‒
Слайд 11Задача №8
9. На рисунке изображён график функции y = f(x). Найдите
[-4;3].
Ответ: функция принимает наибольшее значение при х = 3.
3
-4
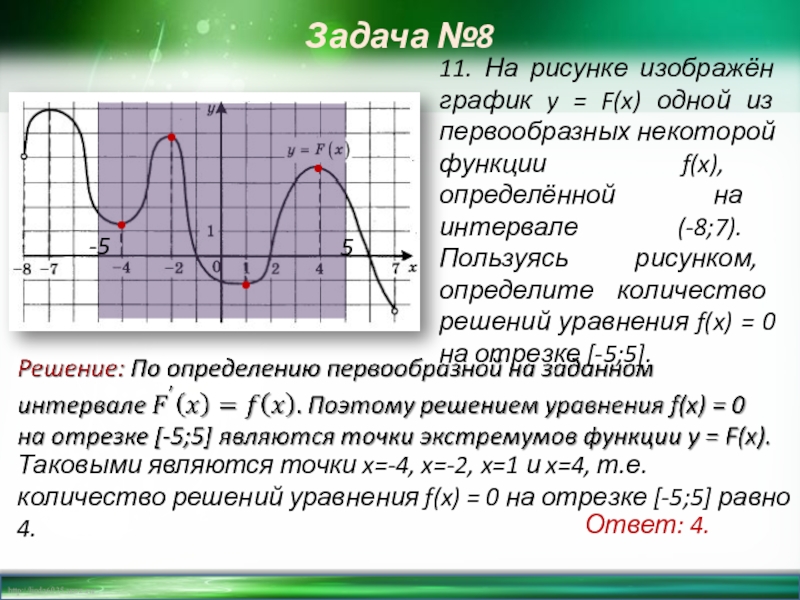
Слайд 13Задача №8
11. На рисунке изображён график y = F(x) одной из
-5
5
•
•
•
•
Таковыми являются точки x=-4, x=-2, x=1 и x=4, т.е. количество решений уравнения f(x) = 0 на отрезке [-5;5] равно 4.
Ответ: 4.
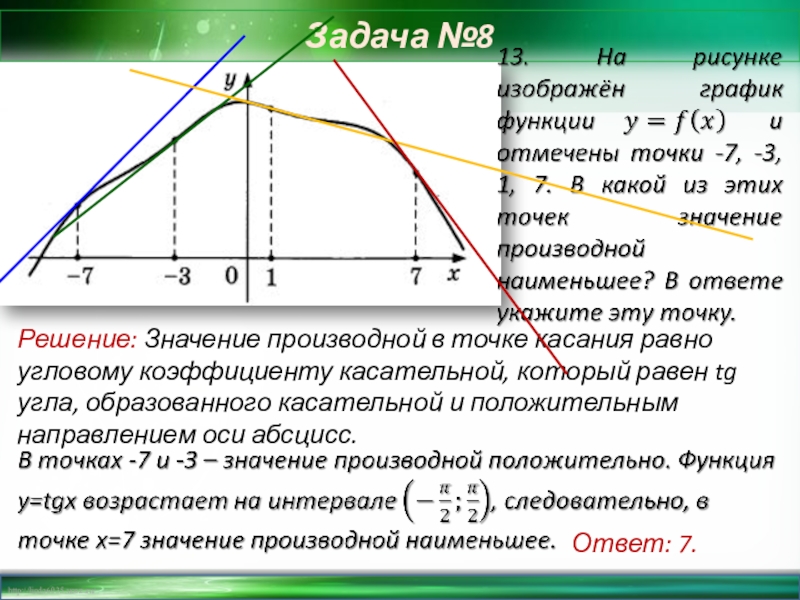
Слайд 15Задача №8
Решение: Значение производной в точке касания равно угловому коэффициенту касательной,
Ответ: 7.
Слайд 17Задача №8
15. На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой
Решение: Если производная меняет знак с плюса на минус, т.е. возрастание функции сменяется убыванием, то эта точка является точкой максимума функции.
•
Т.е. x = - 2 – точка максимума.
Ответ: -2
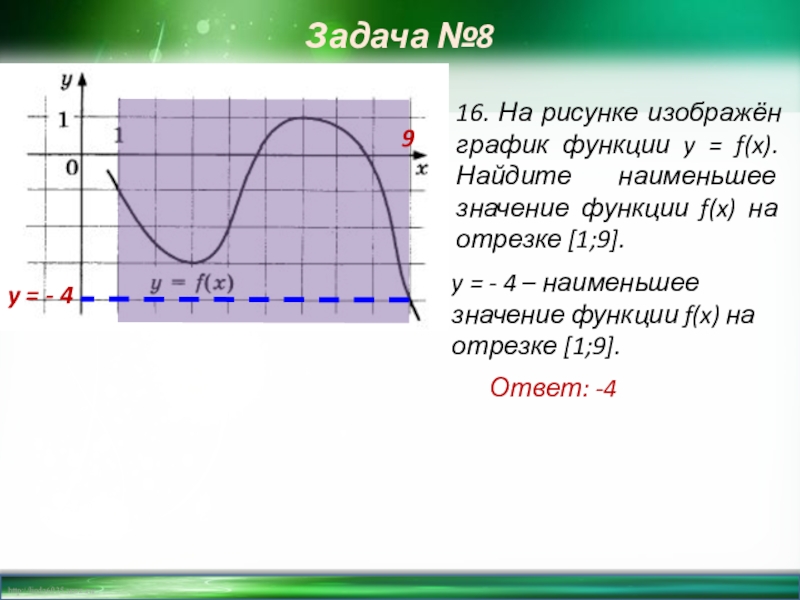
Слайд 18Задача №8
16. На рисунке изображён график функции y = f(x). Найдите
y = - 4
9
y = - 4 – наименьшее значение функции f(x) на отрезке [1;9].
Ответ: -4
Слайд 19Задача №8
В каждой точке интервала убывания дифференцируемой на этом интервале функции
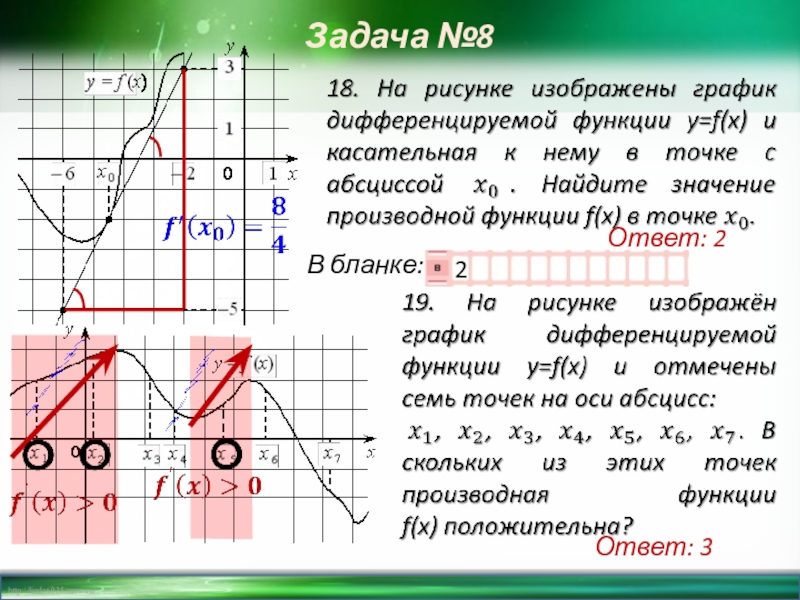
Ответ: 2
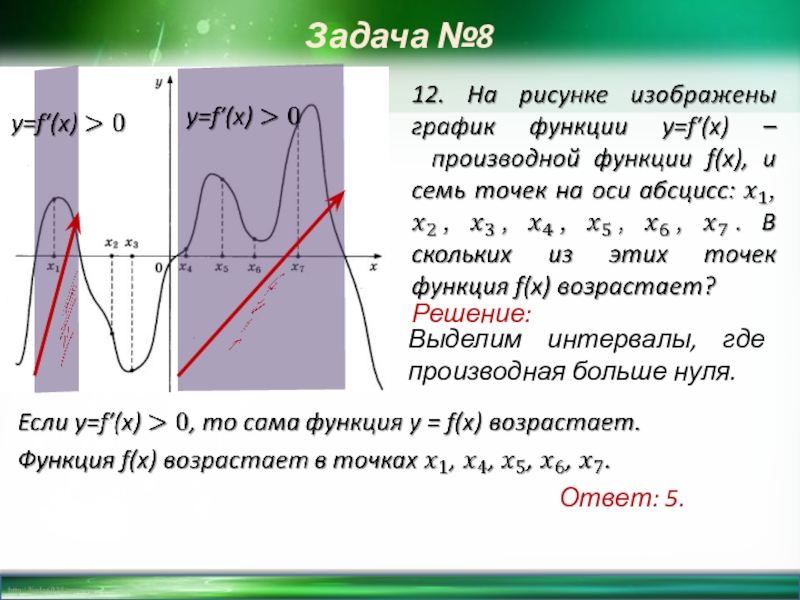
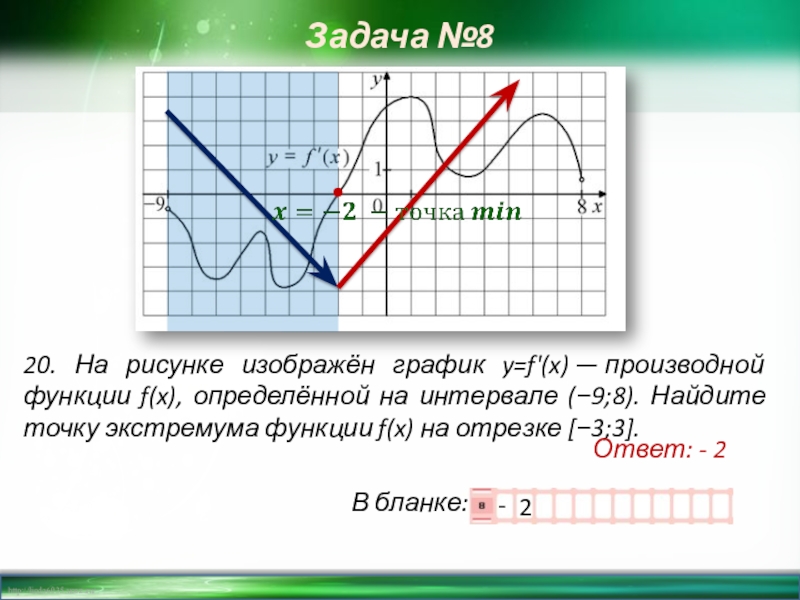
Слайд 2120. На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале
Ответ: - 2
Задача №8
-
•
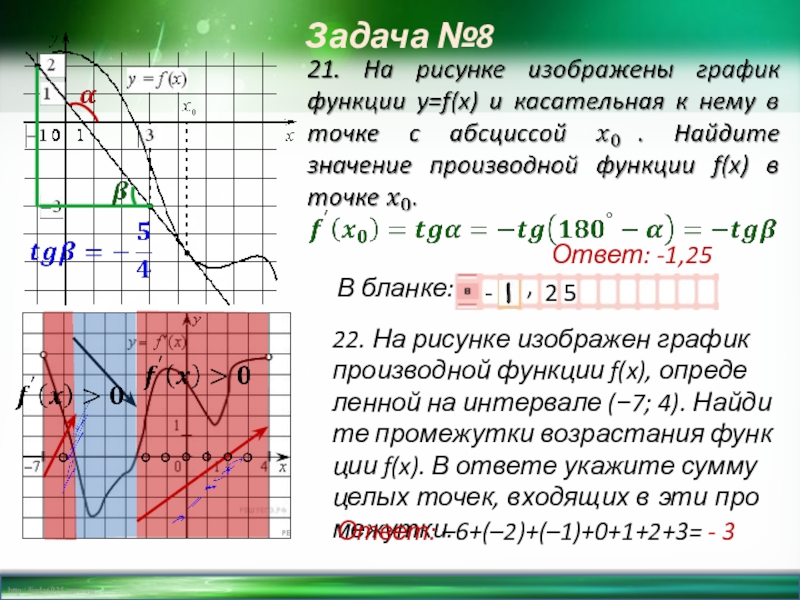
Слайд 22Ответ: -1,25
22. На рисунке изображен график производной функции f(x), определенной на
Ответ: –6+(–2)+(–1)+0+1+2+3= - 3
Задача №8
,
5
2
-
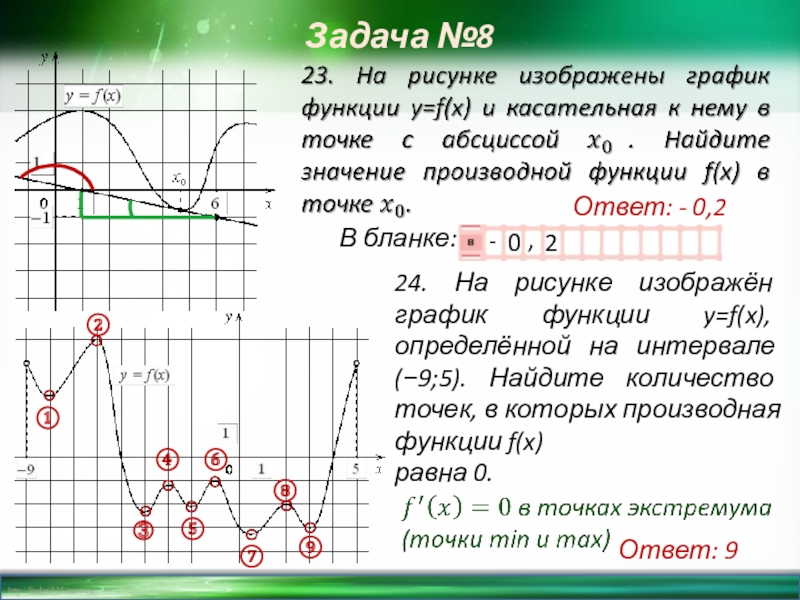
Слайд 2324. На рисунке изображён график функции y=f(x), определённой на интервале (−9;5).
равна 0.
Ответ: - 0,2
Ответ: 9
Задача №8
①
②
③
④
⑤
⑥
⑦
⑧
⑨
Слайд 2425. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале
Ответ: - 2
26. На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (−3;8). Найдите точку минимума функции f(x).
Ответ: 4
Задача №8
-2
3
4
Слайд 2729. На рисунке изображен график y=f′(x) — производной функции f(x), определенной на
Задача №8
Точки графика функции f(x), принадлежащих отрезку [−10;10] являются точками экстремума, если график производной этой функции пересекает ось абсцисс, т.е. в этом случае происходит смена знака производной и характера монотонности.
Таких точек на рисунке 5: х = -6, х=-2, х=2, х=6, х=9.
Ответ: 5
˅
˅
˅
˅
˅
Слайд 28Задача №8
30. На рисунке изображен график y=f′(x) — производной функции y=f(x),
4
6
Длина наибольшего промежутка возрастания функции y=f(x) равна 6.
Ответ: 6
Слайд 29Задача №8
http://reshuege.ru/
ЕГЭ 2015. Математика. 30 вариантов типовых тестовых заданий и 800
http://opengia.ru/subjects/mathematics-11/topics/4?page=169
Источник шаблона: Фокина Лидия Петровна, учитель начальных классов, МКОУ «СОШ ст. Евсино» Искитимского района Новосибирской области, сайт http://linda6035.ucoz.ru/
Использованные источники












![Презентация по математике на тему Задача №8 ЕГЭ-2015 по математике, профильный уровень 25. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале 25. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (−8;4). В какой точке отрезка [−2;3] функция](/img/thumbs/98993e9a6a7c2c89693f1495b6f1220b-800x.jpg)