- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Цилиндр
Содержание
- 1. Презентация по математике на тему Цилиндр
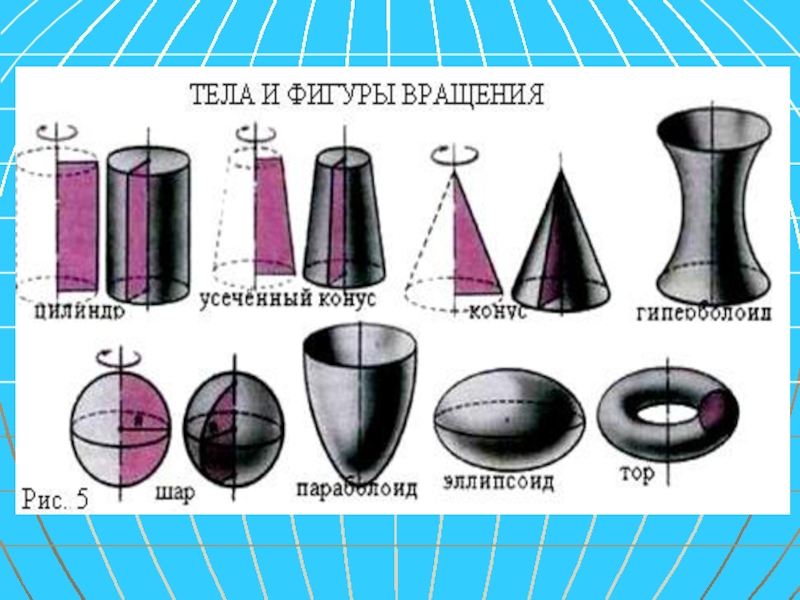
- 2. Тела вращения — объёмные тела, возникающие при вращении
- 3. Слайд 3
- 4. цилиндр
- 5. Примеры моделей цилиндра в окружающей жизни
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Цили́ндр— геометрическое тело, состоящее из двух кругов,
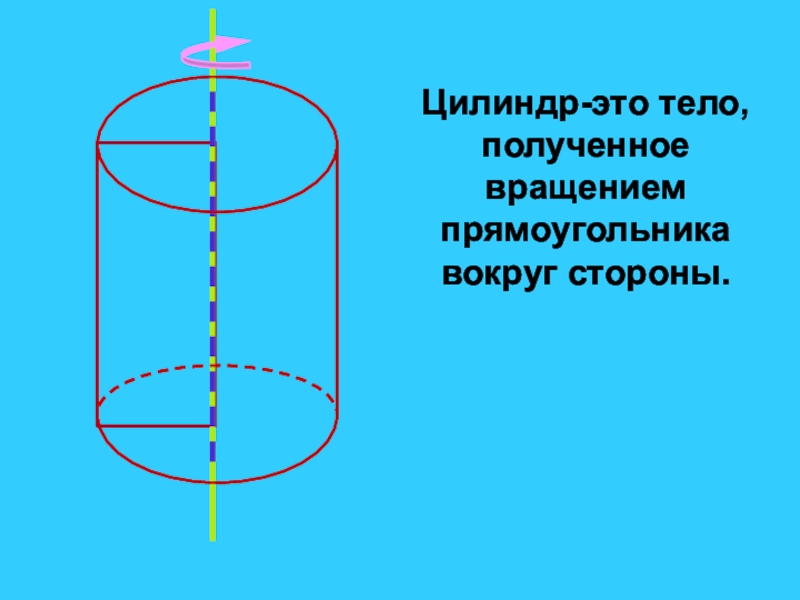
- 19. Цилиндр-это тело, полученное вращением прямоугольника вокруг стороны.
- 20. Элементы цилиндра. 12341. Основания цилиндра2. Образующие L(H-высота)3.Ось цилиндра4. Радиус основания (R)
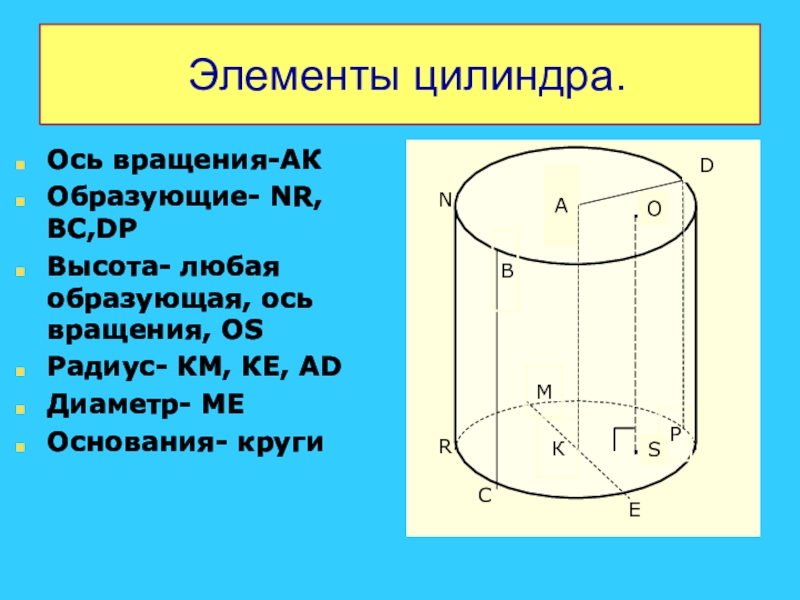
- 21. Элементы цилиндра.АВСDЕКPMNRОсь вращения-АКОбразующие- NR, BC,DРВысота- любая образующая, ось вращения, OSРадиус- КМ, КЕ, АDДиаметр- МЕОснования- кругиSO
- 22. Слайд 22
- 23. Площадь поверхности цилиндраSп.п.= 2Sосн.+Sб.п.Sосн.=ПR2 Sб.п.=2ПRHSп.п.=2ПR2+2ПRHSп.п.=2ПR(R+H)
- 24. Решим задачуДиагональ развёртки боковой поверхности цилиндра составляет
- 25. Разверткой боковой поверхности является прямоугольник АА1В1В.
- 26. Осевое сечение цилиндра – квадрат, диагональ
- 27. Найти: Sп.п. Решение: Н=АВ=16см, R=АD=20смSп.п. =
- 28. ЗадачаЦилиндр получается вращением прямоугольника со сторонами 16
- 29. Тест по теме: «Цилиндр. Площадь его поверхности и объем»
- 30. Вопрос №1: По какой формуле можно вычислить боковую поверхность цилиндра?а) 2πRHб) 2πR(H+R)в) πR2H
- 31. Вопрос №2: По какой формуле можно вычислить полную поверхность цилиндра?а) πR2Hб) 2πRH в) 2πR(H+R)
- 32. Вопрос №7: Вычислите боковую поверхность данного цилиндра.а) 15π см2б) 30π см2в) 48π см23см5см3см
- 33. Вопрос №4: Вычислите полную поверхность данного цилиндра.а) 32π см2б) 24π см2в) 16π см22см6см
- 34. Правильные ответыНа оценку «5»-8 правильных ответов.На оценку
- 35. Задачи
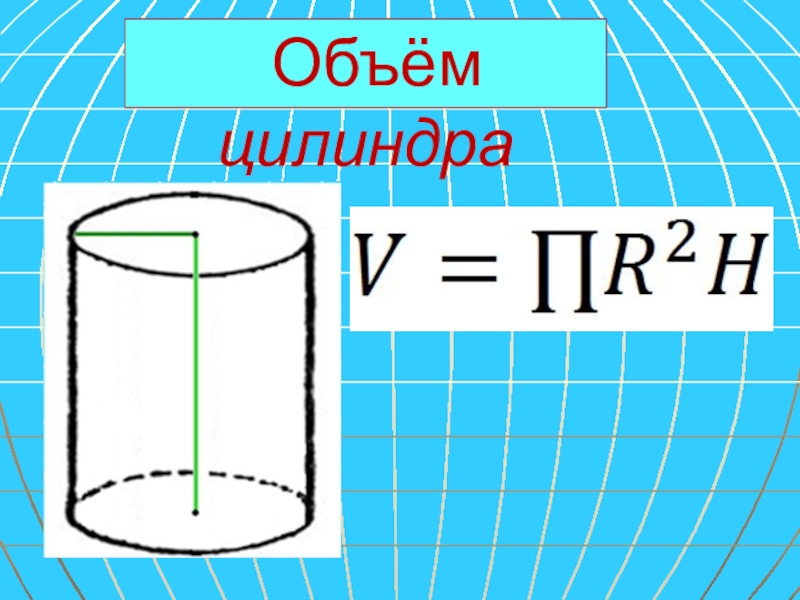
- 36. Объём цилиндра
- 37. Вопрос №1: По какой формуле можно вычислить объем цилиндра?а) 2πR2Hб) πRH2 в) πR2H
- 38. Вопрос №2: Вычислите объем данной емкости. а) 6250π см3б) 2500π см3в) 250π см310см25 см
- 39. Благодарю за внимание!!!
Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры вокруг оси, лежащей в той же плоскости.
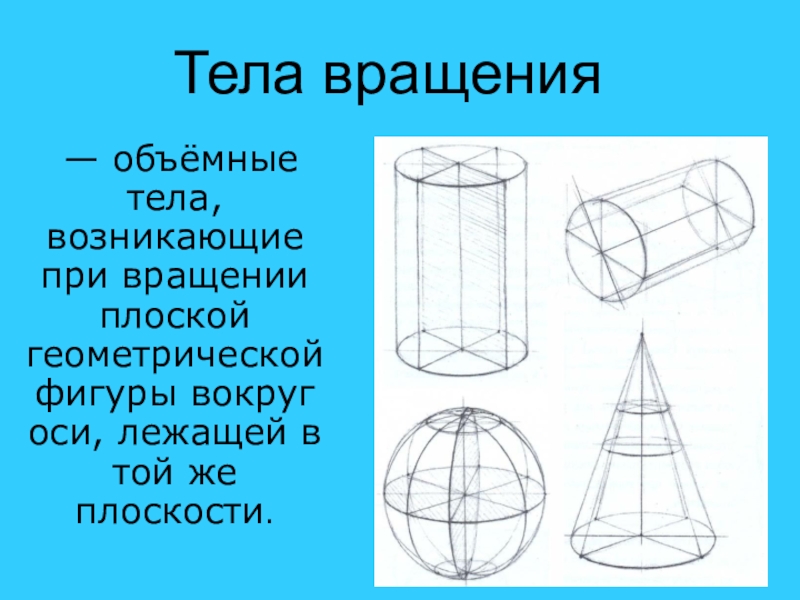
Слайд 2Тела вращения
— объёмные тела, возникающие при вращении плоской геометрической фигуры вокруг
оси, лежащей в той же плоскости.
Слайд 18
Цили́ндр— геометрическое тело, состоящее из двух кругов, лежащих в параллельных плоскостях(основания)
, и отрезков, соединяющих точки окружностей (боковая поверхность).
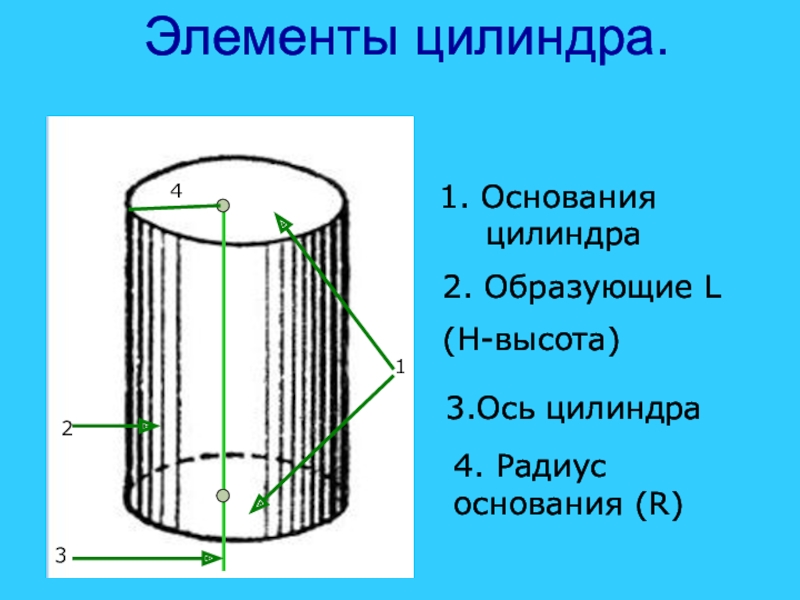
Слайд 20Элементы цилиндра.
1
2
3
4
1. Основания цилиндра
2. Образующие L
(H-высота)
3.Ось цилиндра
4. Радиус
основания (R)
Слайд 21Элементы цилиндра.
А
В
С
D
Е
К
P
M
N
R
Ось вращения-АК
Образующие- NR, BC,DР
Высота- любая образующая, ось вращения, OS
Радиус- КМ,
КЕ, АD
Диаметр- МЕ
Основания- круги
Диаметр- МЕ
Основания- круги
S
O
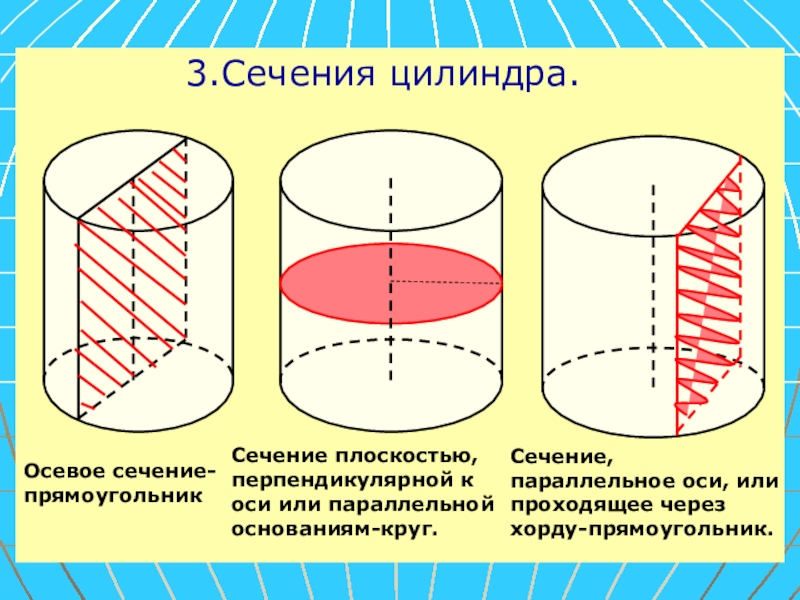
Слайд 22 3.Сечения цилиндра.
Осевое сечение-прямоугольник
Сечение плоскостью,
перпендикулярной к оси или параллельной основаниям-круг.
Сечение, параллельное оси, или проходящее через хорду-прямоугольник.
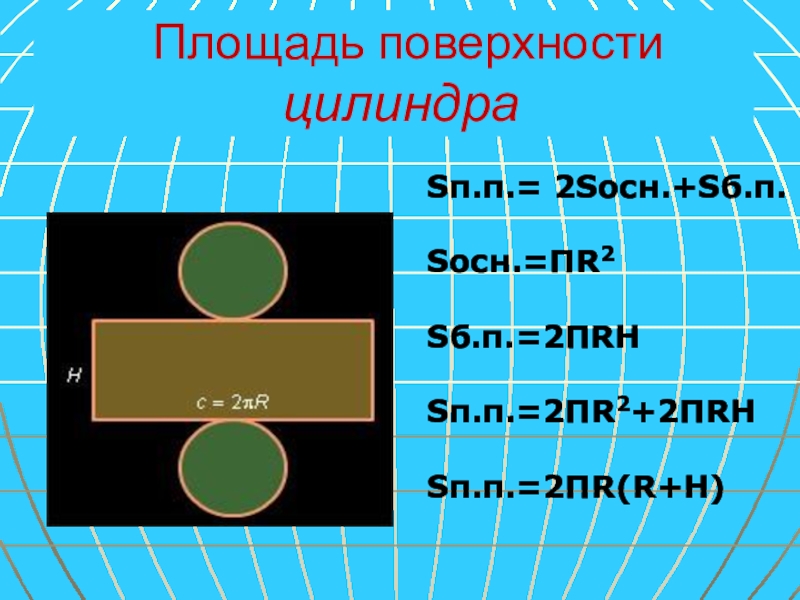
Слайд 23 Площадь поверхности цилиндра
Sп.п.= 2Sосн.+Sб.п.
Sосн.=ПR2
Sб.п.=2ПRH
Sп.п.=2ПR2+2ПRH
Sп.п.=2ПR(R+H)
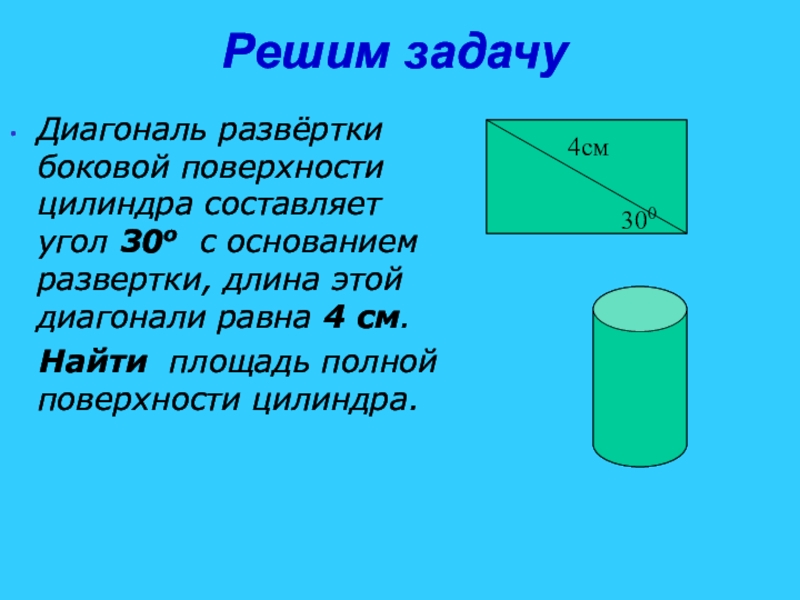
Слайд 24Решим задачу
Диагональ развёртки боковой поверхности цилиндра составляет угол 30о с основанием
развертки, длина этой диагонали равна 4 см.
Найти площадь полной поверхности цилиндра.
Найти площадь полной поверхности цилиндра.
300
4см
Слайд 25Разверткой боковой поверхности является прямоугольник АА1В1В.
Из прямоугольного треугольника АА1В
находим
B1
B
A
A1
Далее имеем
Sп.п.= R(R + H) =
Ответ:
4см
300
Слайд 26
Осевое сечение цилиндра – квадрат, диагональ которого равна 20см. Найти
высоту цилиндра, площадь основания, площадь боковой поверхности.
Решение: АА1В1В – квадрат. АВ=ВВ1
АВ1=20см. АВ12=АВ2+ВВ12
Ответ:
(см2).
ЗАДАЧА
Слайд 27
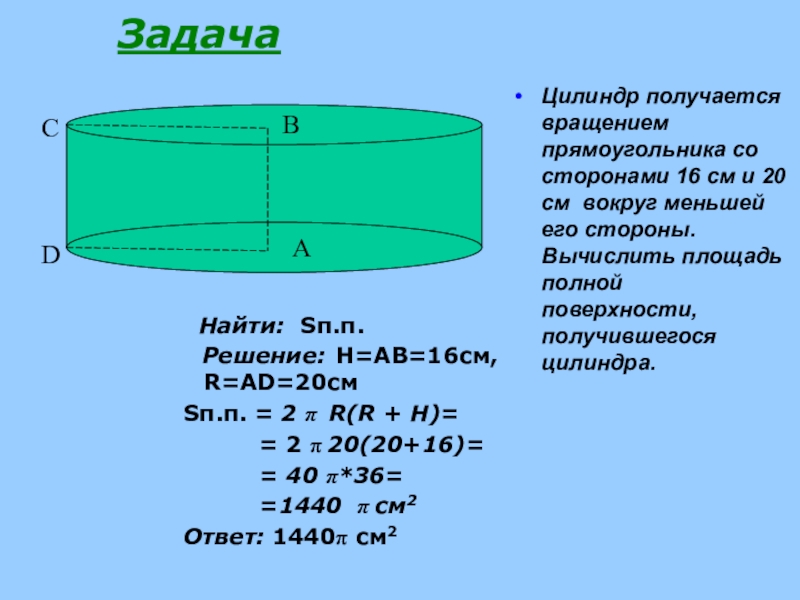
Найти: Sп.п.
Решение: Н=АВ=16см, R=АD=20см
Sп.п. = 2 R(R +
Н)=
= 2 20(20+16)=
= 40 *36=
=1440 см2
Ответ: 1440 см2
= 2 20(20+16)=
= 40 *36=
=1440 см2
Ответ: 1440 см2
А
В
С
D
Цилиндр получается вращением прямоугольника со сторонами 16 см и 20 см вокруг меньшей его стороны. Вычислить площадь полной поверхности, получившегося цилиндра.
Задача
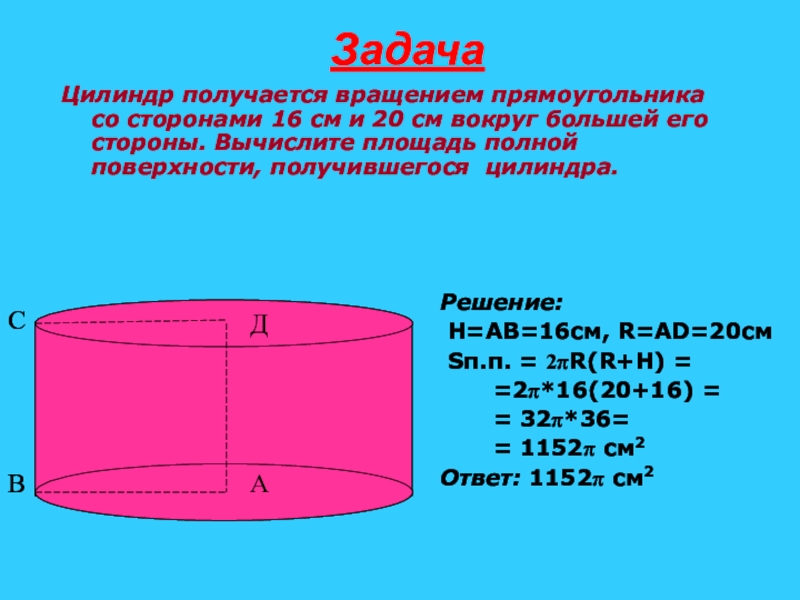
Слайд 28Задача
Цилиндр получается вращением прямоугольника со сторонами 16 см и 20 см
вокруг большей его стороны. Вычислите площадь полной поверхности, получившегося цилиндра.
Д
С
В
А
Решение:
Н=АВ=16см, R=АD=20см
Sп.п. = R(R+Н) =
=2*16(20+16) =
= 32*36=
= 1152 см2
Ответ: 1152 см2
Слайд 30Вопрос №1:
По какой формуле можно вычислить боковую поверхность цилиндра?
а) 2πRH
б) 2πR(H+R)
в)
πR2H
Слайд 31Вопрос №2:
По какой формуле можно вычислить полную поверхность цилиндра?
а) πR2H
б) 2πRH
в) 2πR(H+R)
Слайд 32Вопрос №7:
Вычислите боковую поверхность
данного цилиндра.
а) 15π см2
б) 30π см2
в) 48π
см2
3см
5см
3см
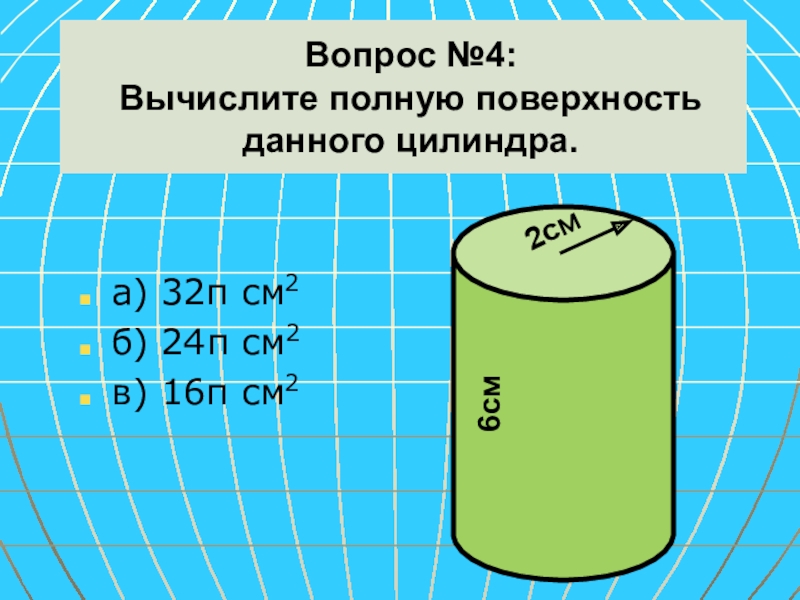
Слайд 33Вопрос №4:
Вычислите полную поверхность
данного цилиндра.
а) 32π см2
б) 24π см2
в) 16π
см2
2см
6см
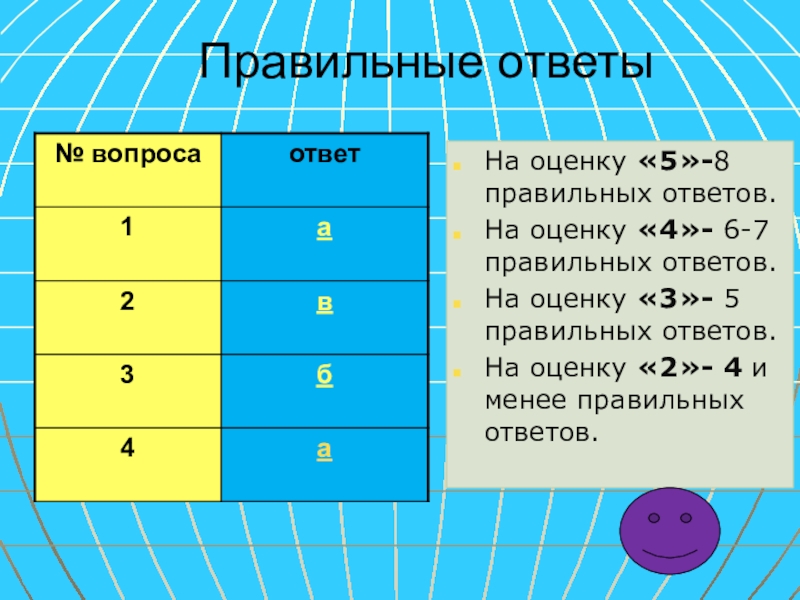
Слайд 34Правильные ответы
На оценку «5»-8 правильных ответов.
На оценку «4»- 6-7 правильных ответов.
На
оценку «3»- 5 правильных ответов.
На оценку «2»- 4 и менее правильных ответов.
На оценку «2»- 4 и менее правильных ответов.
