- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему трапеция
Содержание
- 1. Презентация по математике на тему трапеция
- 2. ПовторениеНазовите свойства площадей многоугольников1. Равные многоугольники имеют
- 3. ПовторениеА ВСДНМДано:АВСД – равнобедренная трапецияВН, СМ –
- 4. 2. Площадь прямоугольника АВСД равна 26 .
- 5. Площадь прямоугольного треугольникаАВС 1. Дано: АВС
- 6. Решение задач из открытого банка задачНайдите площадь
- 7. Решение задач из открытого банка задачНайдите площадь
- 8. Решение задач из открытого банка задачНайти площади четырёхугольников
- 9. Изучение нового материала Площадь параллелограмма
- 10. Предложите вывод формулы площади параллелограммаАВСДКМКакие свойства площадей
- 11. Вспомните, как выводили формулу площади прямоугольного
- 12. Площадь трапеции АВСДЕFЗапишите на доске и в
- 13. Решение задач из открытого банка задач, с
- 14. Домашнее задание & 2, п. 51,
- 15. Открытый банк задач http://mathege.ru/or/ege/Main 1). Стороны
- 16. 5). Основание трапеции равно 13, высота равна
- 17. Вдохновение нужно в поэзии, как и в
Слайд 1Площадь параллелограмма, треугольника, трапеции
Панчиева Камиля
Ученицы 8 «б» класса
МБОУСОШ №2
Слайд 2Повторение
Назовите свойства площадей многоугольников
1. Равные многоугольники имеют равные площади
2. Если многоугольник
3. Площадь квадрата равна квадрату его стороны
Слайд 3Повторение
А
В
С
Д
Н
М
Дано:
АВСД – равнобедренная трапеция
ВН, СМ – высоты трапеции
S (АВН) =
Найти: S (АВСД)
Решение:
АВСД- равнобедренная трапеция, следовательно, АВН = ДСМ, а значит, по свойству 1 имеем :
S( АВН) = S (ДСМ)
2. По свойству 2 : S (АВСД) = S ( АВН) + S (НВСМ) + S (МСД)
3. S (АВСД) = 5 + 15 + 5 = 25
Ответ : 25
Слайд 42. Площадь прямоугольника АВСД равна 26 . Найдите площадь треугольника АВД.
А
В
С
Д
Решение:
1. Проведём диагональ ВД
2. АВД = СДВ, сл- но,
S ( АВД) = S ( ДСВ), а значит, S ( АВСД) = 2S ( АВД)
3. S ( АВД) = 26 : 2 = 13
Какой вывод вы можете сделать о нахождении площади прямоугольного треугольника?
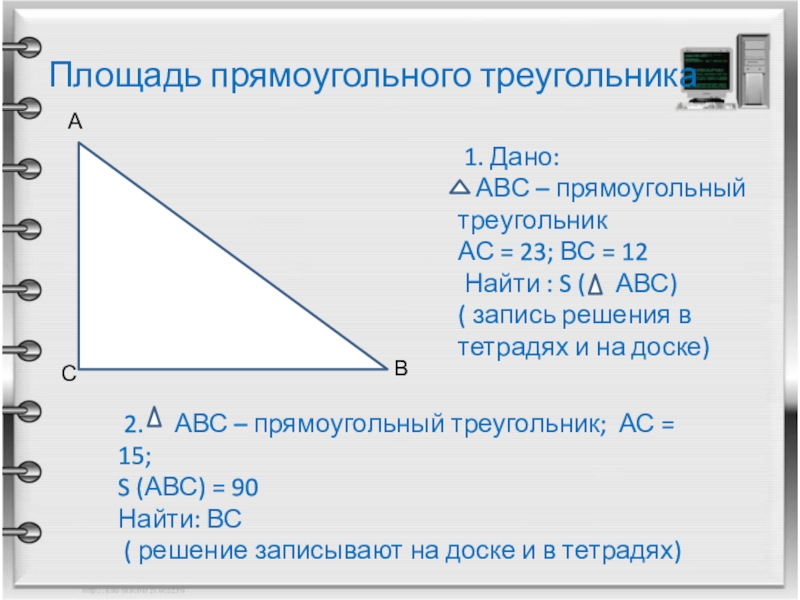
Слайд 5Площадь прямоугольного треугольника
А
В
С
1. Дано:
АВС – прямоугольный треугольник
АС =
Найти : S ( АВС)
( запись решения в тетрадях и на доске)
2. АВС – прямоугольный треугольник; АС = 15;
S (АВС) = 90
Найти: ВС
( решение записывают на доске и в тетрадях)
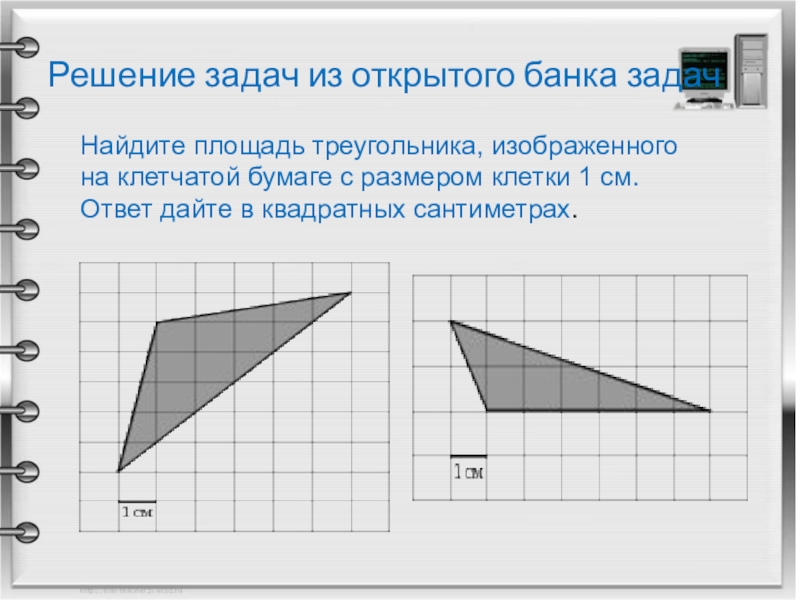
Слайд 6Решение задач из открытого банка задач
Найдите площадь треугольника, изображенного на клетчатой
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см * 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Слайд 7Решение задач из открытого банка задач
Найдите площадь треугольника, изображенного на клетчатой
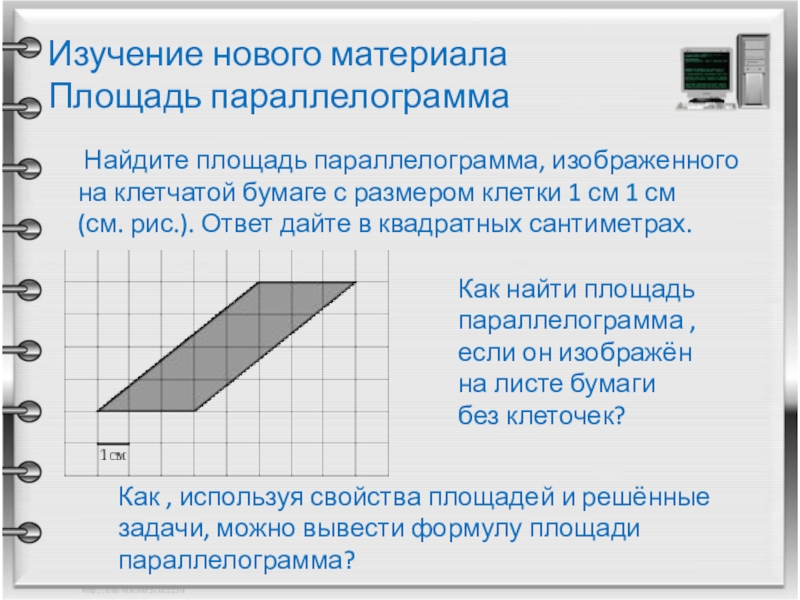
Слайд 9Изучение нового материала
Площадь параллелограмма
Найдите площадь параллелограмма, изображенного на
Как найти площадь параллелограмма , если он изображён на листе бумаги без клеточек?
Как , используя свойства площадей и решённые задачи, можно вывести формулу площади параллелограмма?
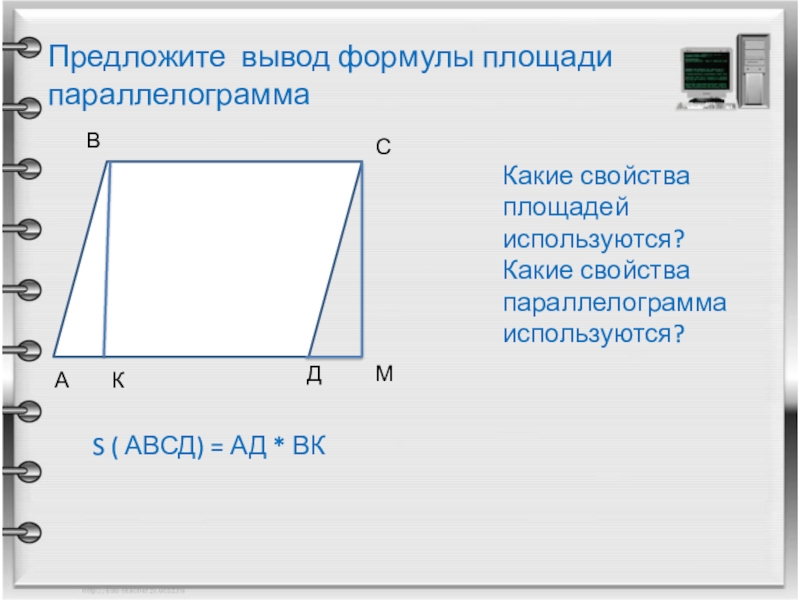
Слайд 10Предложите вывод формулы площади параллелограмма
А
В
С
Д
К
М
Какие свойства площадей используются?
Какие свойства параллелограмма используются?
S
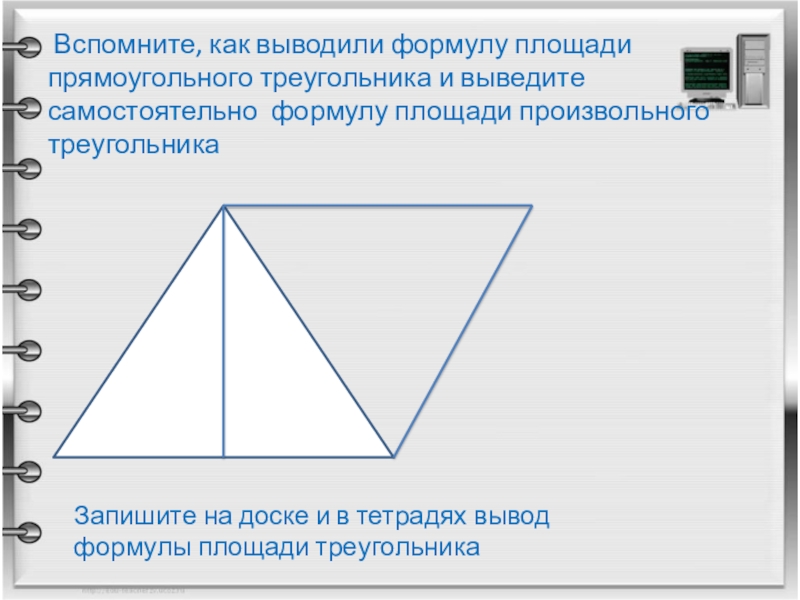
Слайд 11 Вспомните, как выводили формулу площади прямоугольного треугольника и выведите самостоятельно
Запишите на доске и в тетрадях вывод формулы площади треугольника
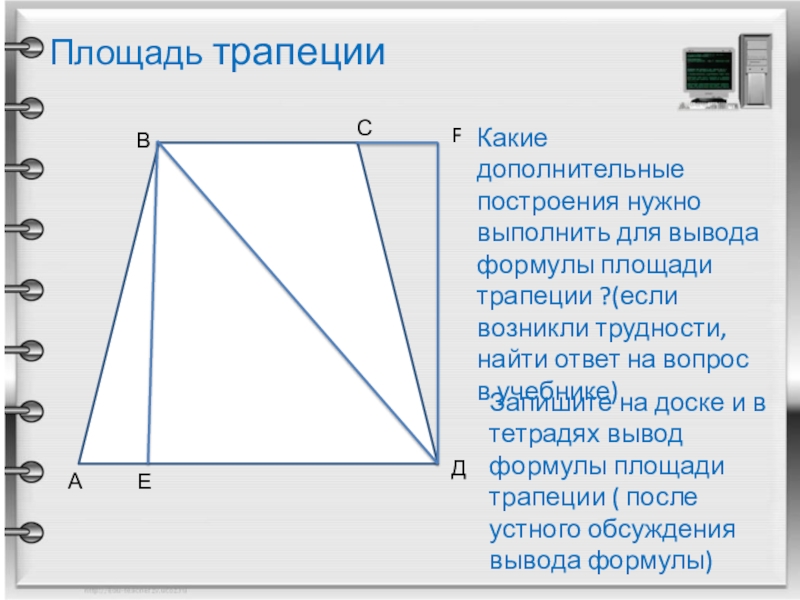
Слайд 12Площадь трапеции
А
В
С
Д
Е
F
Запишите на доске и в тетрадях вывод формулы площади
Какие дополнительные построения нужно выполнить для вывода формулы площади трапеции ?(если возникли трудности, найти ответ на вопрос в учебнике)
Слайд 13Решение задач из открытого банка задач,
с использованием формул
Найдите (в
Слайд 15Открытый банк задач
http://mathege.ru/or/ege/Main
1). Стороны параллелограмма равны 9 и 15.
2). Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
3). У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
4). Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.
Слайд 165). Основание трапеции равно 13, высота равна 5, а площадь равна
6). Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45.
7). Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150. Найдите площадь трапеции.
Слайд 17
Вдохновение нужно в поэзии, как и в геометрии
Нет царского пути к геометрии.
( Евклид)