Выполнила: Гуржапова Регина
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Способы нахождения площадей фигур на клетчатой бумаге
Содержание
- 1. Презентация по математике на тему Способы нахождения площадей фигур на клетчатой бумаге
- 2. Цель исследования: Изучить способы решения задач
- 3. .Гипотеза: если геометрическая фигура изображена на клетчатой
- 4. Георг Алекса́ндр Пик (18591859 — 1942) — австрийский математик Широкую известность получила открытая
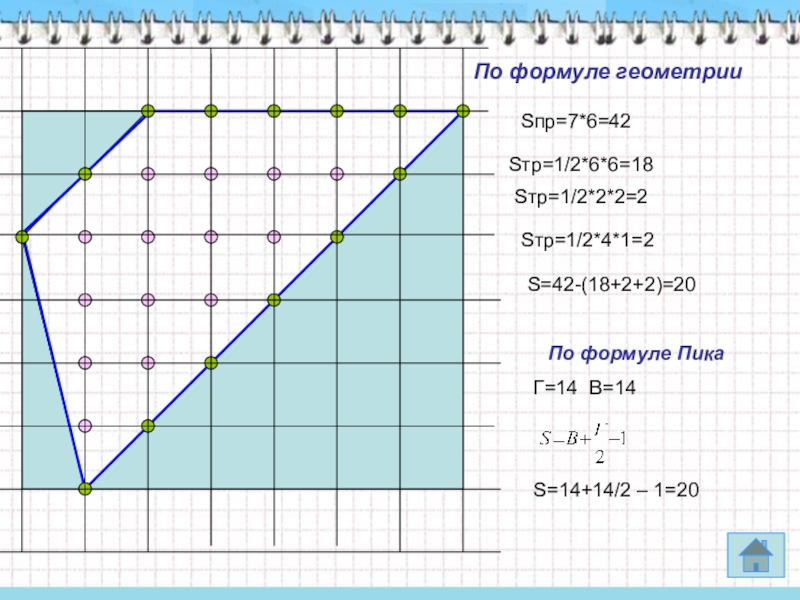
- 5. Sпр=7*6=42По формуле ПикаГ=14 В=14S=14+14/2 – 1=20S=42-(18+2+2)=20По формуле геометрии
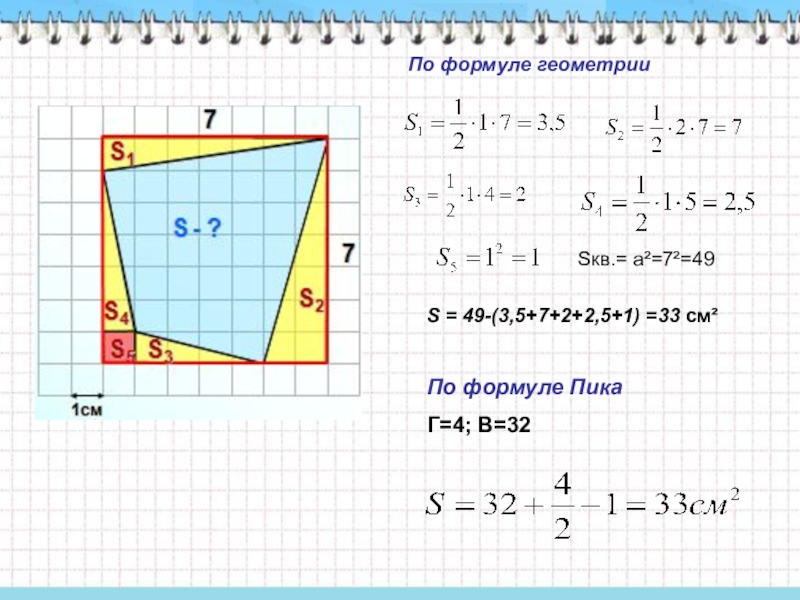
- 6. По формуле Пика Г=4; В=32По формуле геометрииSкв.= a²=7²=49S = 49-(3,5+7+2+2,5+1) =33 см²
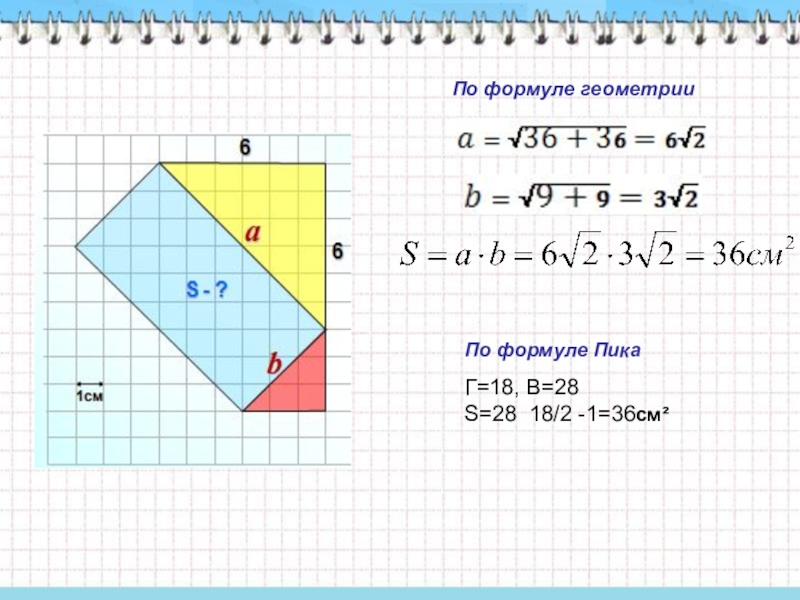
- 7. Г=18, В=28S=28 18/2 -1=36см² По формуле геометрииПо формуле Пика
- 8. Г=18;В=28.S=28+18/2 -1=36см² По формуле геометриисм²По формуле Пика
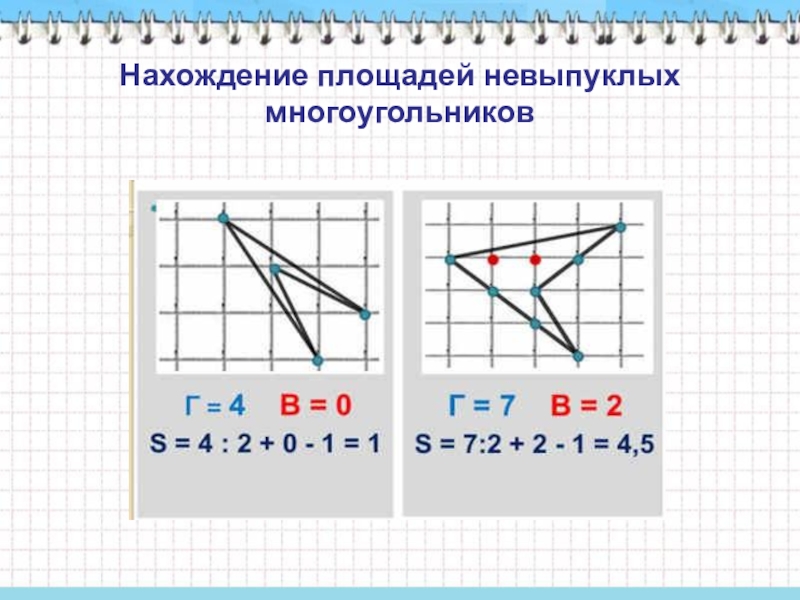
- 9. Нахождение площадей невыпуклых многоугольников
- 10. Практические задачиПоможет нам формула Пика и для
- 11. Эксперимент
- 12. Вывод : в результате проделанной работы:
- 13. Заключение В процессе
- 14. Слайд 14
Цель исследования: Изучить способы решения задач на клетчатой бумаге и выбрать самый лучший.Задачи:Изучить литературу по теме исследования.Выбрать и изучить способы нахождения площадей фигур на клетчатой бумаге. Подобрать задачи.Провести эксперимент.Сделать выводы по результатам работы. Объект исследования: фигуры
Слайд 1Способы нахождения площадей фигур на клетчатой бумаге
МАОУ «Хамнейская средняя общеобразовательная школа»
Исследовательская
работа
Слайд 2 Цель исследования:
Изучить способы решения задач на клетчатой бумаге
и выбрать самый лучший.
Задачи:
Изучить литературу по теме исследования.
Выбрать и изучить способы нахождения площадей фигур на клетчатой бумаге. Подобрать задачи.
Провести эксперимент.
Сделать выводы по результатам работы.
Объект исследования: фигуры на клетчатой бумаге.
Предмет исследования: площадь фигур.
Методы исследования:
1. теоретический: изучение литературы;
2. эмпирический: эксперимент, анализ, сравнение;
3. математический: построения, вычисления.
Задачи:
Изучить литературу по теме исследования.
Выбрать и изучить способы нахождения площадей фигур на клетчатой бумаге. Подобрать задачи.
Провести эксперимент.
Сделать выводы по результатам работы.
Объект исследования: фигуры на клетчатой бумаге.
Предмет исследования: площадь фигур.
Методы исследования:
1. теоретический: изучение литературы;
2. эмпирический: эксперимент, анализ, сравнение;
3. математический: построения, вычисления.
Слайд 3
.
Гипотеза:
если геометрическая фигура изображена на клетчатой бумаге, то её площадь
можно вычислить различными способами и убедиться, что результаты вычислений будут одинаковыми.
.
.
Слайд 4Георг Алекса́ндр Пик (18591859 — 1942) — австрийский математик
Широкую известность получила открытая им в 1899 году теорема
Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники.
Слайд 10Практические задачи
Поможет нам формула Пика и для решения геометрических задач с
практическим содержанием, когда объект изображен на клетчатой бумаге в
масштабе.
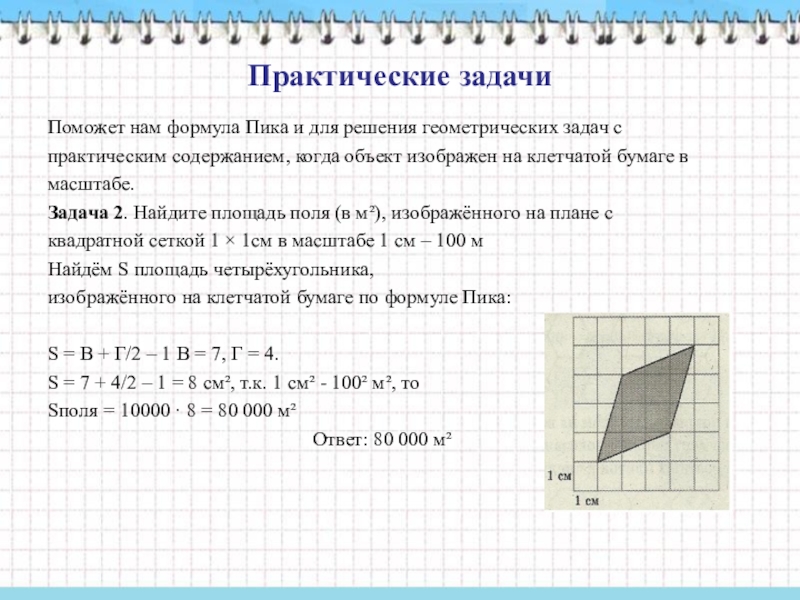
Задача 2. Найдите площадь поля (в м²), изображённого на плане с
квадратной сеткой 1 × 1см в масштабе 1 см – 100 м
Найдём S площадь четырёхугольника,
изображённого на клетчатой бумаге по формуле Пика:
S = В + Г/2 – 1 В = 7, Г = 4.
S = 7 + 4/2 – 1 = 8 см², т.к. 1 см² - 100² м², то
Sполя = 10000 · 8 = 80 000 м²
Ответ: 80 000 м²
Слайд 12Вывод : в результате проделанной работы:
гипотеза подтвердилась: «если
геометрическая фигура изображена на клетчатой бумаге, то её площадь можно вычислить различными способами и убедиться, что результаты вычислений будут одинаковыми».
Практическая значимость: результаты можно использовать на уроках геометрии, для подготовки к ОГЭ и ЕГЭ
Слайд 13Заключение
В процессе исследования я изучила
справочную, научно-популярную литературу. Узнала , что задача на нахождение площади многоугольника с вершинами в узлах сетки подвигла австрийского математика Пика в 1899 году доказать замечательную формулу Пика.
В результате данной работы я расширила свои знания о решении задач на клетчатой бумаге, определила для себя классификацию исследуемых задач, убедилась в их многообразии.
Я научилась вычислять площади многоугольников, нарисованных на клетчатом листке и пришла к выводу, что тема, которая меня заинтересовала, достаточно многогранна, задачи на клетчатой бумаге многообразны, методы и приёмы их решения также разнообразны.
В результате данной работы я расширила свои знания о решении задач на клетчатой бумаге, определила для себя классификацию исследуемых задач, убедилась в их многообразии.
Я научилась вычислять площади многоугольников, нарисованных на клетчатом листке и пришла к выводу, что тема, которая меня заинтересовала, достаточно многогранна, задачи на клетчатой бумаге многообразны, методы и приёмы их решения также разнообразны.
Слайд 14
Литература
1.Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.
2.Задачи открытого банка заданий по математике ФИПИ, 2018
3.В.В.Вавилов, А.В.Устинов .Многоугольники на решетках.М.МЦНМО,2006.
4.Л.С.Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др.Геометрия .7-9 классы.М. Просвещение ,2010
5.Смирнова И., Смирнов В. Геометрия на клетчатой бумаге. М.: Чистые пруды, 2007.
6.Григорьева Г. И. Подготовка школьников к олимпиадам по математике: 5 – 6 классы. Метод. пособие. – М.: Глобус, 2009.
