классов
Нефедова Татьяна Худай – Вергеновна МКОУ «СОШ п.Чернореченский»
2018 год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Совершенствование вычислительных навыков на уроках математики в рамках реализации ФГОС
Содержание
- 1. Презентация по математике на тему Совершенствование вычислительных навыков на уроках математики в рамках реализации ФГОС
- 2. Слайд 2
- 3. Слайд 3
- 4. ЗадачиОпределить наиболее эффективные методы и приёмы формирования
- 5. Слайд 5
- 6. Вычислительный навык – это высокая степень овладения
- 7. Характеристика
- 8. Системный подход Системный подход в работе позволяет
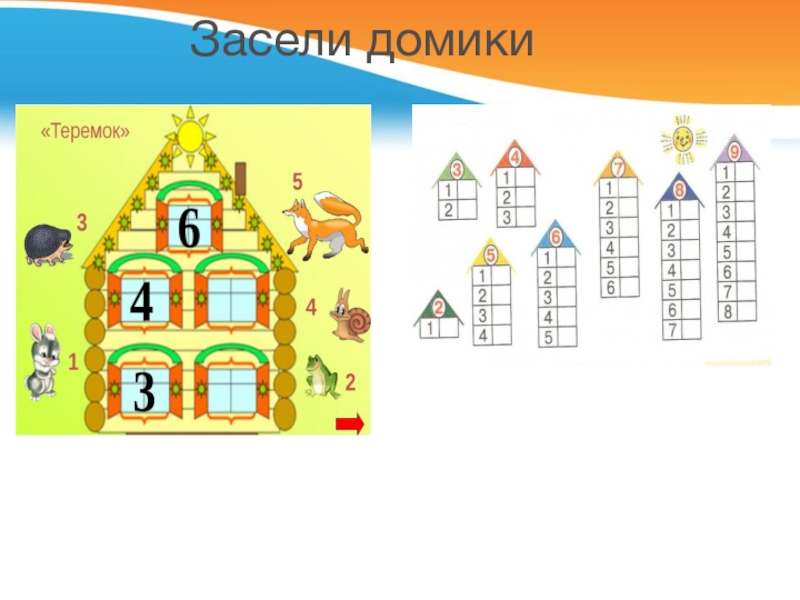
- 9. Засели домики
- 10. Игра «Молчанка»
- 11. Дидактические игры
- 12. Кто в каком домике живёт?
- 13. Картинки - раскраски
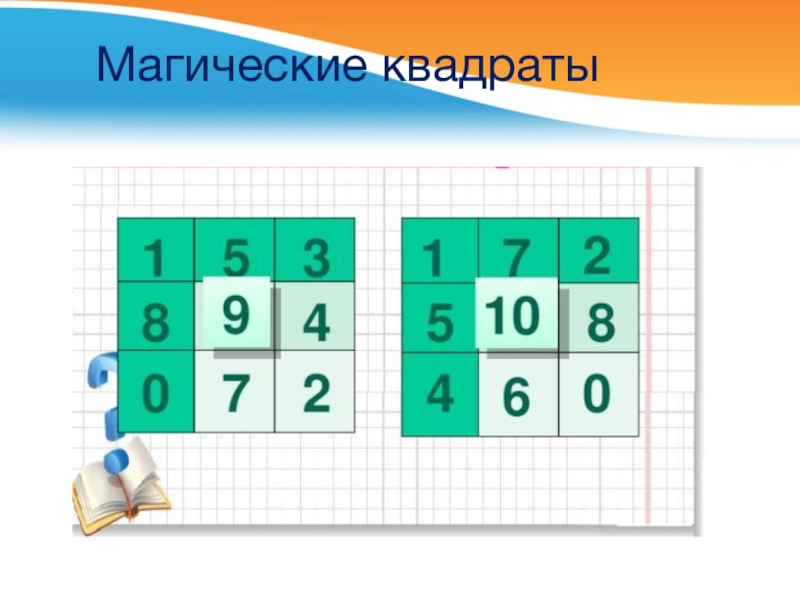
- 14. Магические квадраты
- 15. Задачи в стихотворной форме
- 16. ЛабиринтыИгра
- 17. ЛабиринтыНужно пройти
- 18. Лабиринты
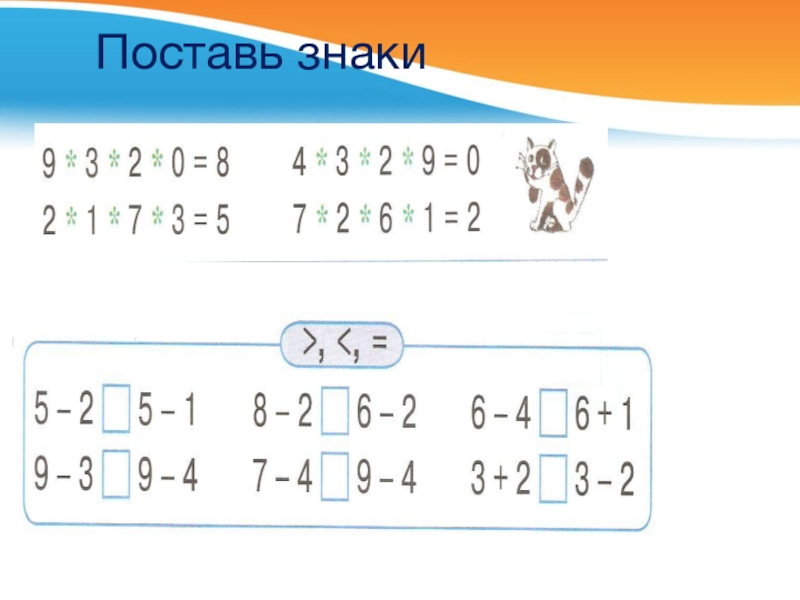
- 19. Поставь знаки
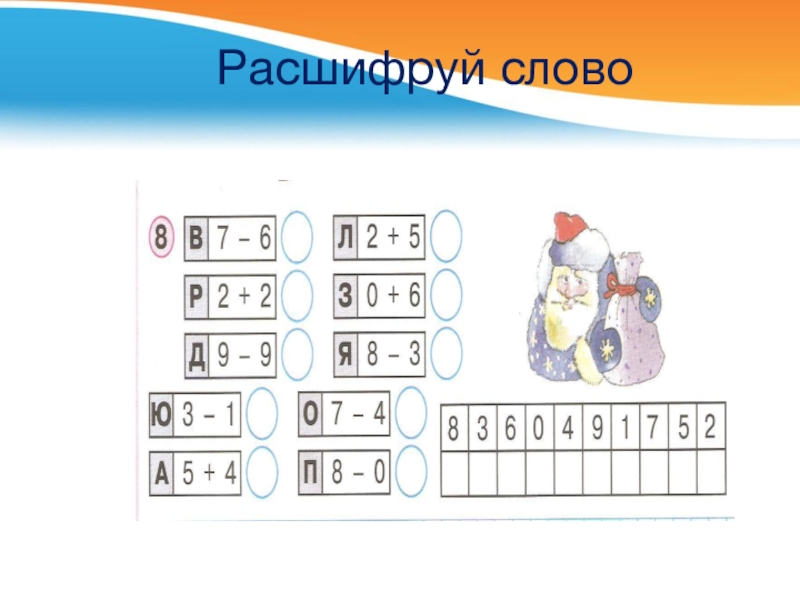
- 20. Расшифруй слово
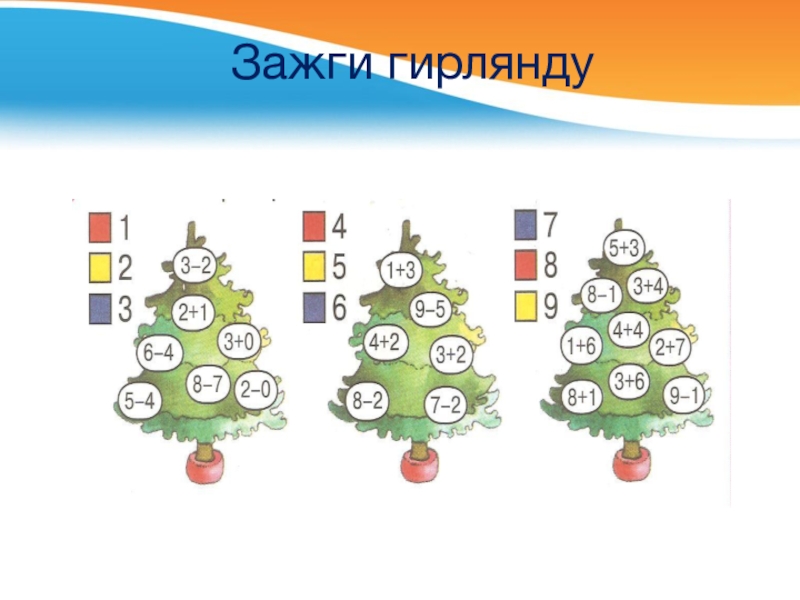
- 21. Зажги гирлянду
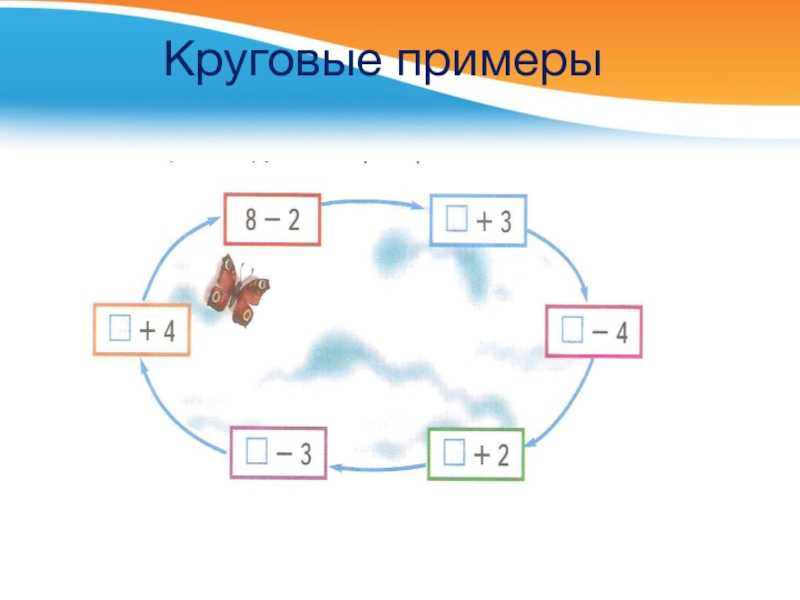
- 22. Круговые примеры
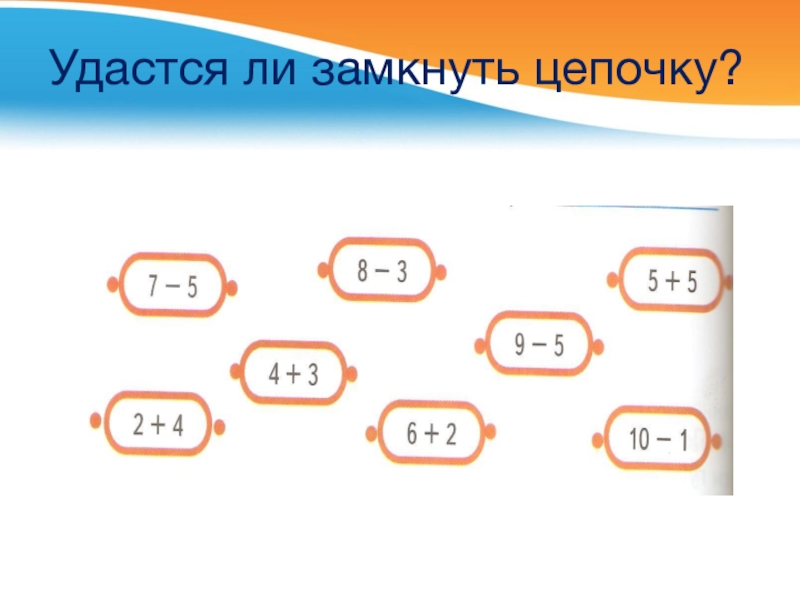
- 23. Удастся ли замкнуть цепочку?
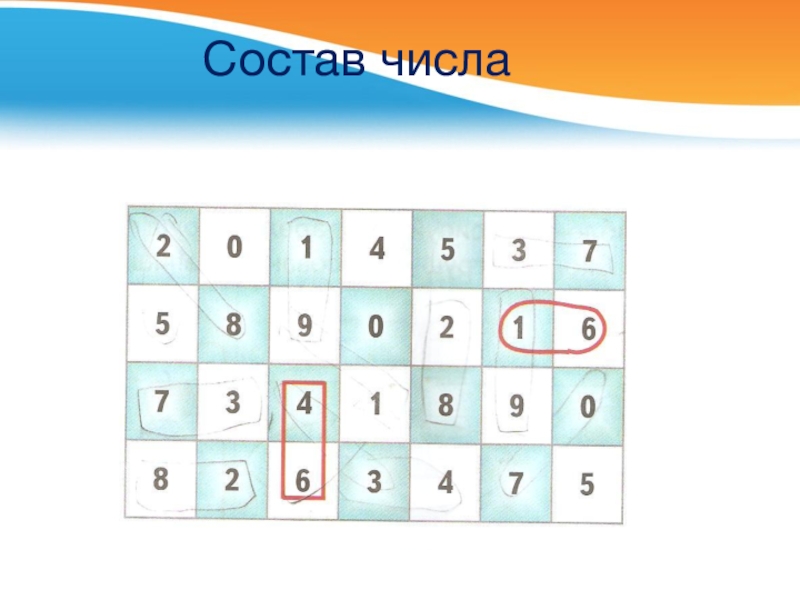
- 24. Состав числа
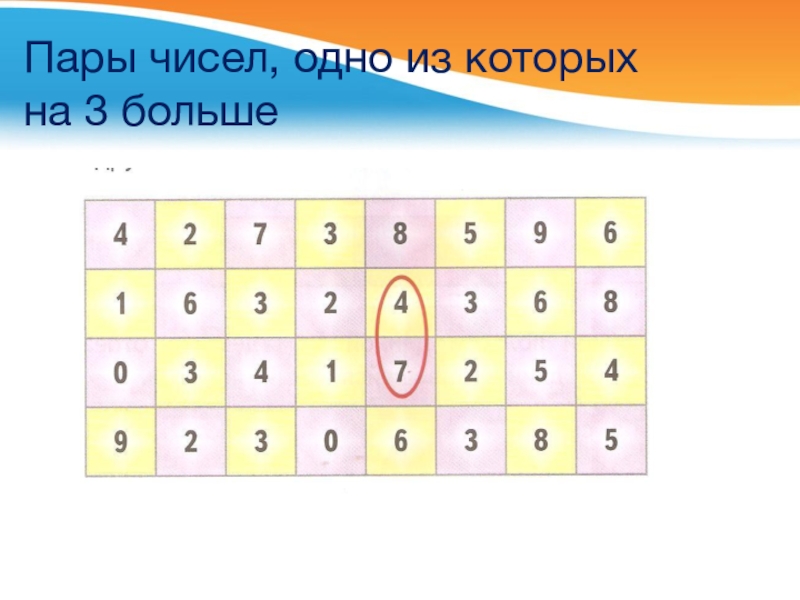
- 25. Пары чисел, одно из которых на 3 больше
- 26. Логические цепочки…5 7 9 … (1 3 5
- 27. Сравнение математических выражений3+4 и 1+6
- 28. Ошибки невидимки10 < 10
- 29. Математические цепочки Это растение каждой бродячей собаке
- 30. Математические цепочкиДетёныши какого животного ещё слепые,
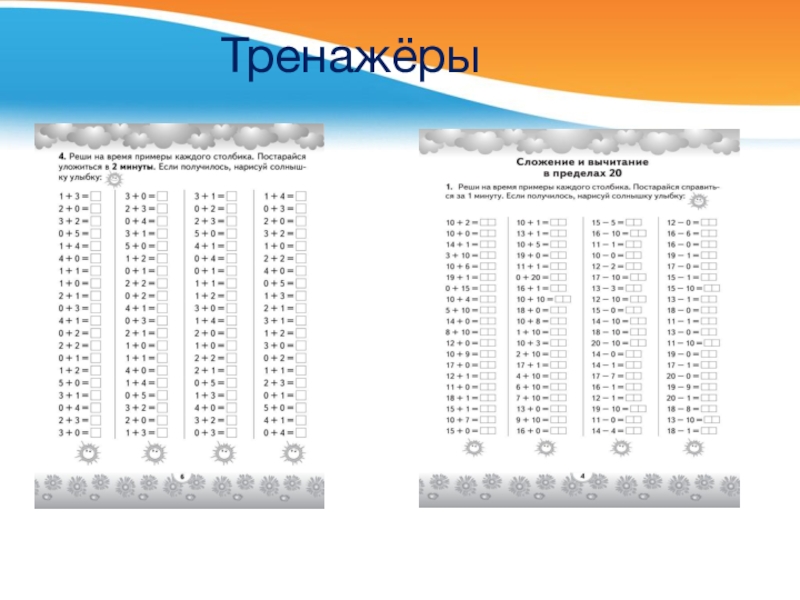
- 31. Тренажёры
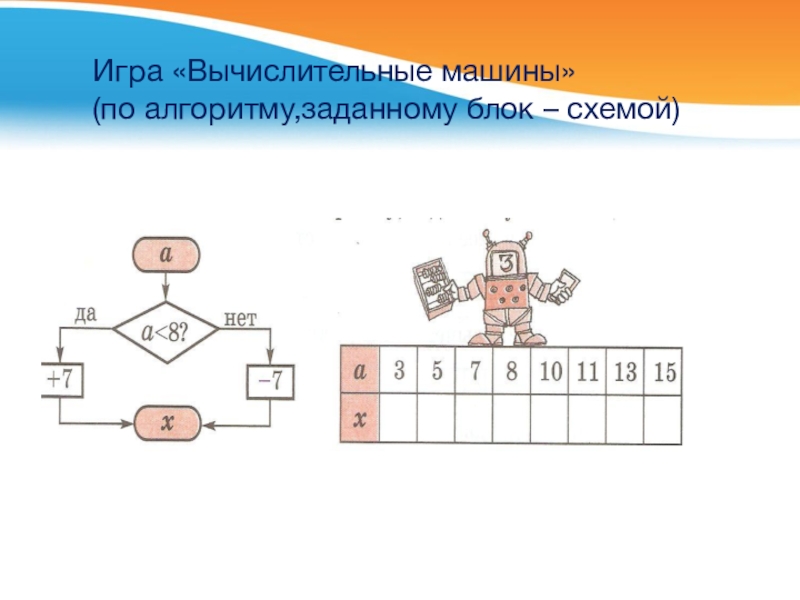
- 32. Игра «Вычислительные машины» (по алгоритму,заданному блок – схемой)
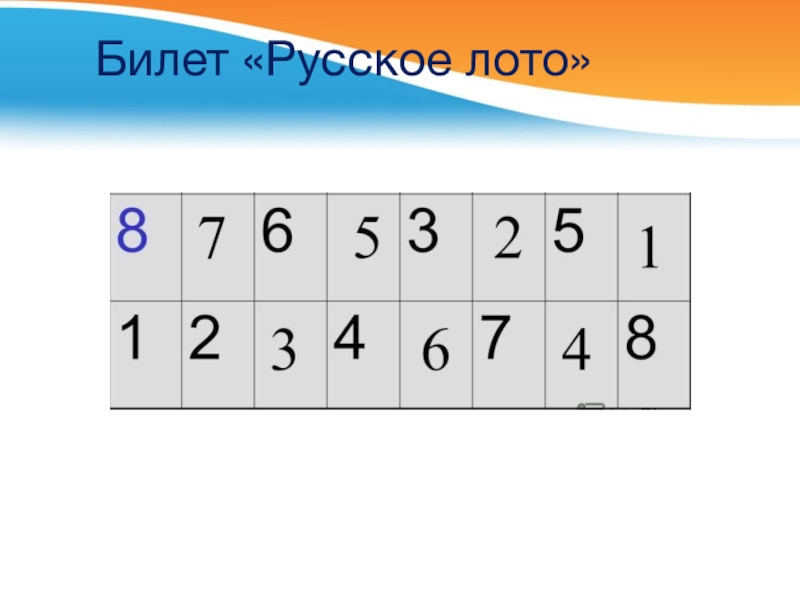
- 33. Билет «Русское лото»
- 34. Математический диктант1. Запишите число, которое следует за
- 35. Тесты
- 36. Цель тестового контроля: Измерить уровень усвоения знаний;Изучить динамику развития личности учащихся;Корректировка процесса обучения
- 37. Слайд 37
Цель: Совершенствование вычислительных навыков на уроке математики в первом классе
Слайд 1Совершенствование вычислительных навыков на уроках математики в рамках реализации ФГОС
Учитель начальных
Слайд 4Задачи
Определить наиболее эффективные методы и приёмы формирования устных вычислительных навыков у
младших школьников для повышения интереса к урокам математики;
Разработать разнообразные виды упражнений для организации устного счёта на уроках математике;
Проследить динамику развития уровня сформированности навыков устного счёта младших школьников
Разработать разнообразные виды упражнений для организации устного счёта на уроках математике;
Проследить динамику развития уровня сформированности навыков устного счёта младших школьников
Слайд 6Вычислительный навык – это высокая степень овладения вычислительными приёмами
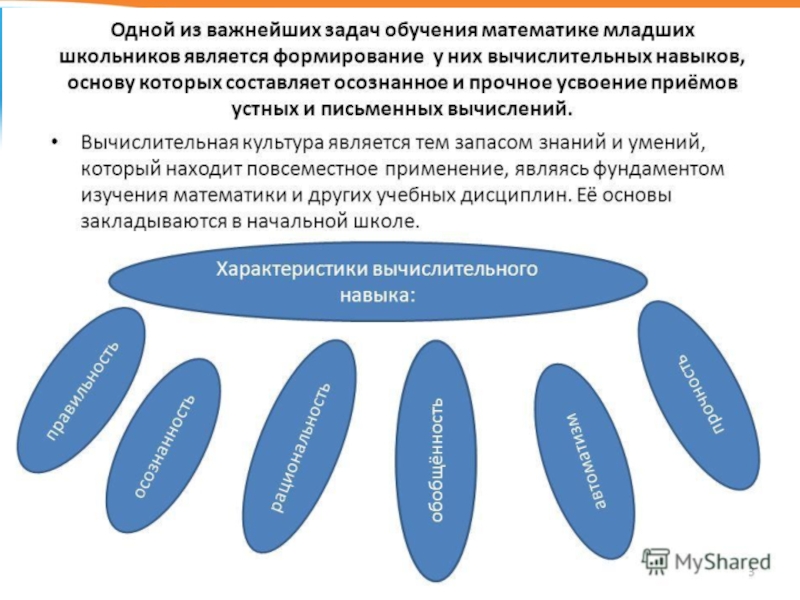
Характеристика
вычислительного навыка:
Осознанность- ученик осознаёт, на основе каких знаний выбраны операции и установлен порядок их выполнения. Это для ученика своего рода доказательства правильности выбора системы операций. Ученик в любой момент может объяснить, как он решал пример и почему можно так решать.
Правильность- ученик правильно находит результат арифметического действия над данными числами ( правильно выбирает и выполняет операции, составляющие приём)
Рациональность- ученик выбирает для данного случая более рациональный приём, т.е. выбирает из возможных операций
Осознанность- ученик осознаёт, на основе каких знаний выбраны операции и установлен порядок их выполнения. Это для ученика своего рода доказательства правильности выбора системы операций. Ученик в любой момент может объяснить, как он решал пример и почему можно так решать.
Правильность- ученик правильно находит результат арифметического действия над данными числами ( правильно выбирает и выполняет операции, составляющие приём)
Рациональность- ученик выбирает для данного случая более рациональный приём, т.е. выбирает из возможных операций
Слайд 7 Характеристика вычислительного навыка
Обобщённость- ученик может
применить приём вычисления к большему числу случаев, т.е. он способен перенести приём вычисления на новые случаи
Автоматизм - ученик выделяет и выполняет операции быстро и в свёрнутом виде
Прочность - ученик сохраняет сформированные вычислительные навыки на длительное время
Автоматизм - ученик выделяет и выполняет операции быстро и в свёрнутом виде
Прочность - ученик сохраняет сформированные вычислительные навыки на длительное время
Слайд 8Системный подход
Системный подход в работе позволяет не только отрабатывать вычислительные
умения, но и нацелен на развитие учащихся.
Система организации диагностики, контроля формирования вычислительных умений и навыков у учащихся, применение компьютерных технологий способствует росту комфортности обучения.
Система организации диагностики, контроля формирования вычислительных умений и навыков у учащихся, применение компьютерных технологий способствует росту комфортности обучения.
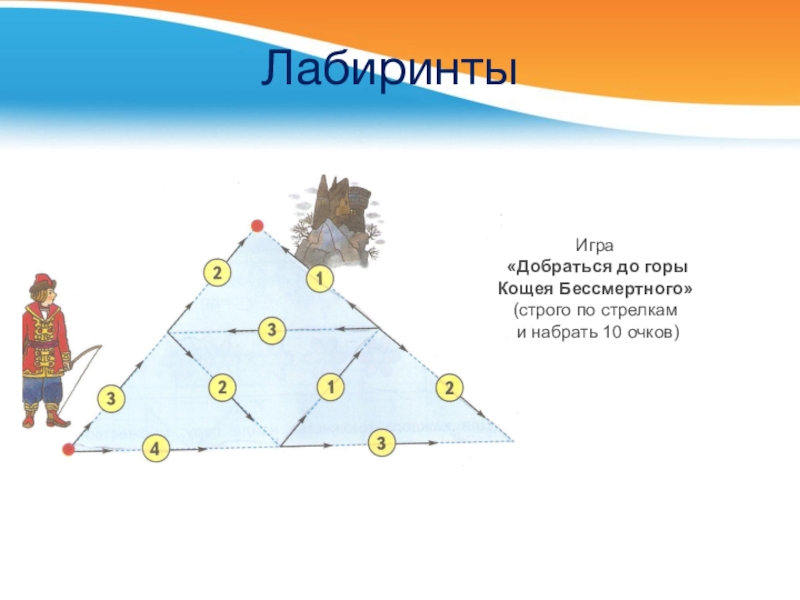
Слайд 16 Лабиринты
Игра
«Добраться до горы
Кощея
Бессмертного»
(строго по стрелкам
и набрать 10 очков)
и набрать 10 очков)
Слайд 17 Лабиринты
Нужно пройти по тем клеточкам лабиринта,
сумма в которых равна 10. Двигаться можно вверх, вниз, влево, вправо, нельзя двигаться по диагонали.
Слайд 26Логические цепочки
…5 7 9 … (1 3 5 7 9 11 13
….)
…5 6 9 10 …(1 2 5 6 9 10 13 14 …)
…21, 17, 13, (…29 25 21 17 13 9 5 1 )
…5 6 9 10 …(1 2 5 6 9 10 13 14 …)
…21, 17, 13, (…29 25 21 17 13 9 5 1 )
Слайд 29Математические цепочки
Это растение каждой бродячей собаке радо. Даже лис, медведей
и волков не боится. Они дерут его клыками, когтями рвут, а растение за них цепляется – расстаться с ними не может. Что это за растение?
7 + 1 + 2 – 9 = ?
Мокрица – 3 Молодило – 2 Репейник – 1
7 + 1 + 2 – 9 = ?
Мокрица – 3 Молодило – 2 Репейник – 1
Слайд 30Математические цепочки
Детёныши какого животного ещё слепые,
а уже умеют защищаться
от врагов?
7 + 1 - 3 - 5 = ?
Крот 1
Ёж 0
Волк 2
7 + 1 - 3 - 5 = ?
Крот 1
Ёж 0
Волк 2
Слайд 34Математический диктант
1. Запишите число, которое следует за числом 2.
2. Запишите число,
которое на 1 больше 6.
3. Уменьши число 4 на 1.
4. Увеличь число 5 на 2.
5. Запиши самое маленькое однозначное число.
6. Запиши предыдущее число для числа 8.
7. Запиши соседей числа 4.
8. Одно число 6, другое 2. Запиши сумму.
9. Сколько надо прибавить к 7, чтобы получилось 9?
10. К двум прибавить столько же.
11. Запиши числа от 3 до 8.
12. Запиши самое большое однозначное число.
13. Шесть котят пили молоко. К ним прибежал ещё один котёнок. Сколько всего стало котят?
14. У Тани 6 кукол, а у Дины на 2 куклы меньше. Сколько кукол у Дины?
15. Вера нашла 3 гриба, а Света на 1 гриб больше. Сколько грибов нашла Света?
3. Уменьши число 4 на 1.
4. Увеличь число 5 на 2.
5. Запиши самое маленькое однозначное число.
6. Запиши предыдущее число для числа 8.
7. Запиши соседей числа 4.
8. Одно число 6, другое 2. Запиши сумму.
9. Сколько надо прибавить к 7, чтобы получилось 9?
10. К двум прибавить столько же.
11. Запиши числа от 3 до 8.
12. Запиши самое большое однозначное число.
13. Шесть котят пили молоко. К ним прибежал ещё один котёнок. Сколько всего стало котят?
14. У Тани 6 кукол, а у Дины на 2 куклы меньше. Сколько кукол у Дины?
15. Вера нашла 3 гриба, а Света на 1 гриб больше. Сколько грибов нашла Света?
Слайд 36Цель тестового контроля:
Измерить уровень усвоения знаний;
Изучить динамику развития личности учащихся;
Корректировка процесса
обучения
Слайд 37 Вывод
Целенаправленная и системная
работа позволяет сформировать высокий уровень вычислительных умений и навыков обучающихся. Они играют большую роль в развитии мышления школьников, их сообразительности, математической зоркости, наблюдательности. Всё это делает новые знания личностно значимыми , развивает учебно -познавательные мотивы учащихся, вырабатывает у них творческий подход к жизни, приучает их вдумчиво относиться к любой выполняемой деятельности, без чего не мыслимо овладеть основами наук, а также почти любым видом практической и профессиональной деятельности.