– 2016 год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Скрещивающие прямые
Содержание
- 1. Презентация по математике на тему: Скрещивающие прямые
- 2. ЦЕЛИ УРОКА: Обучающая цель: Ввести понятие скрещивающихся
- 3. 1.Организация начала занятия.2.Проверка домашнего задания.3.Изучение нового материала.4.Первичное
- 4. Вопросы для повторенияЧто изучает стереометрия?Основные понятия стереометрии.Аксиомы
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Следствия из аксиом ТеоремаЧерез
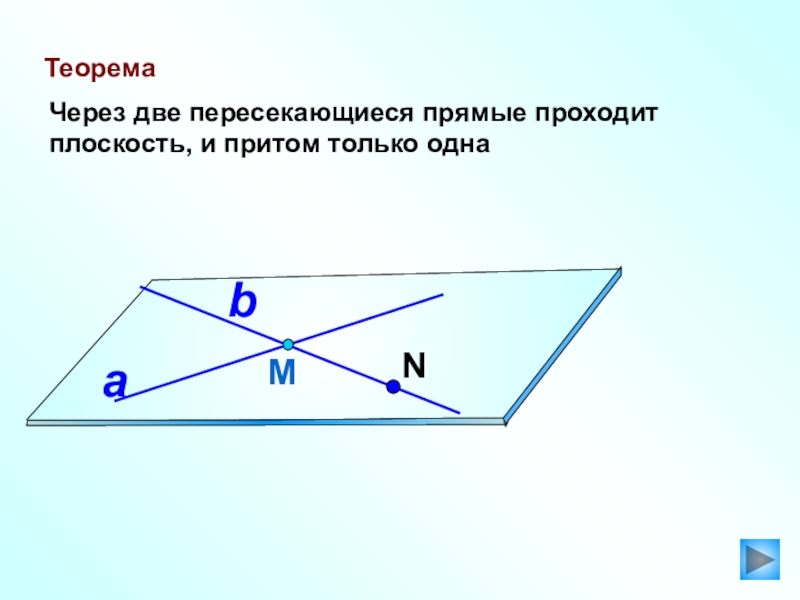
- 11. ТеоремаЧерез две пересекающиеся прямые проходит плоскость, и притом только однаМabN
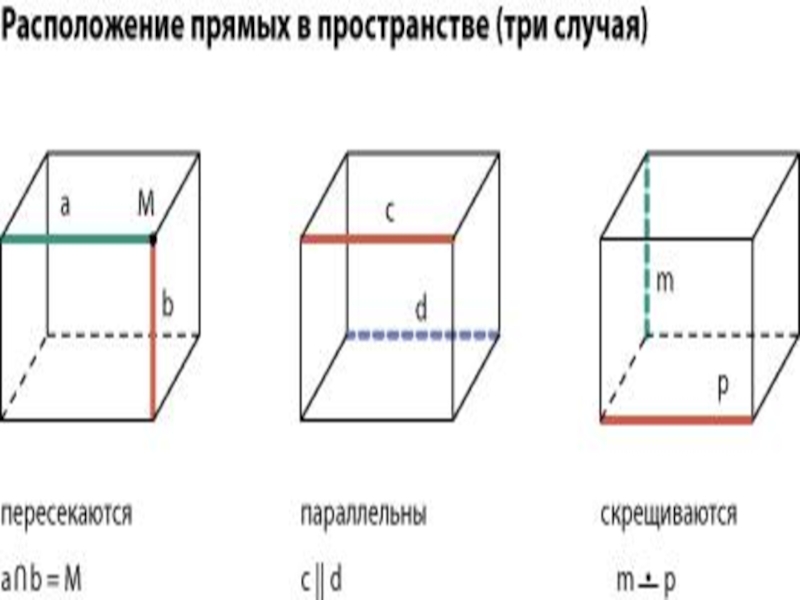
- 12. Расположение двух прямых в пространстве.Они могут лежать
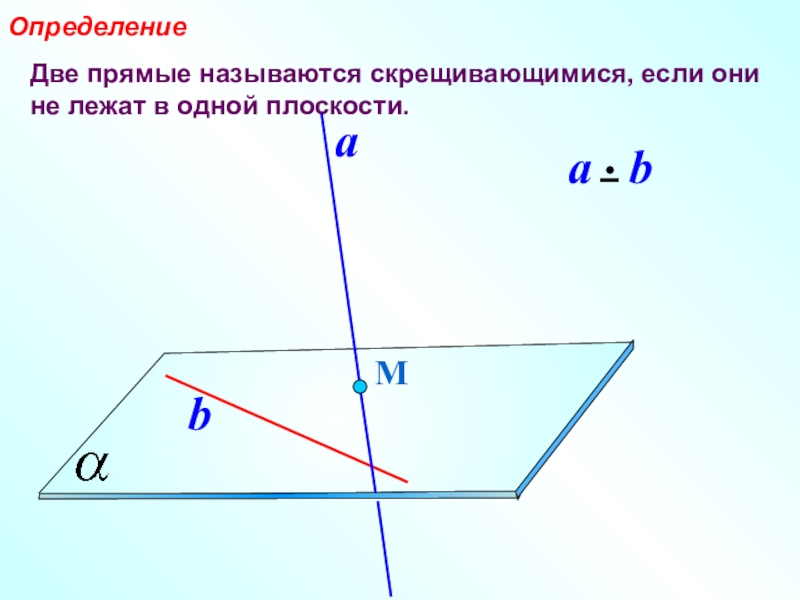
- 13. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.ОпределениеМab
- 14. IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIiНаглядное представление о скрещивающихся прямых дают две
- 15. ab
- 16. Найдите на рисунке параллельные прямые.Назовите параллельные прямые и плоскости.Найдите скрещивающиеся прямые.
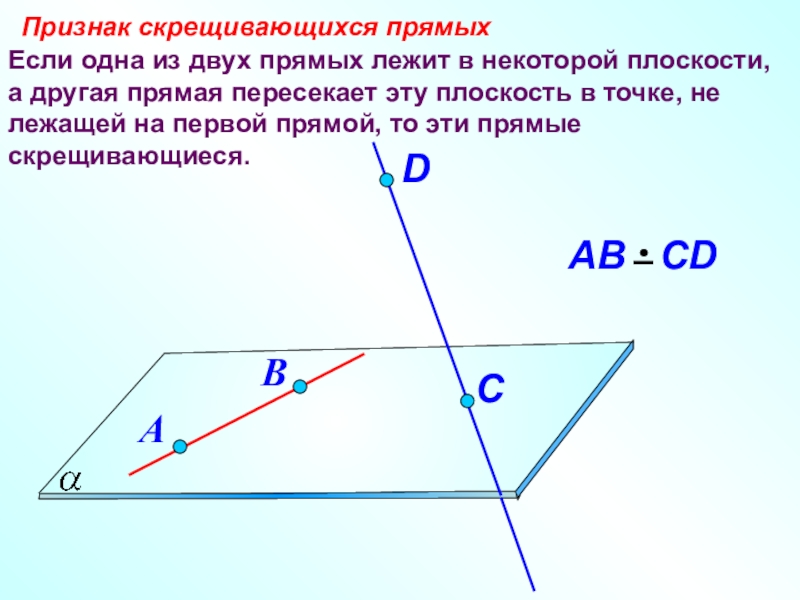
- 17. Если одна из двух прямых лежит в
- 18. Признак скрещивающихся прямых.Дано: АВ α,
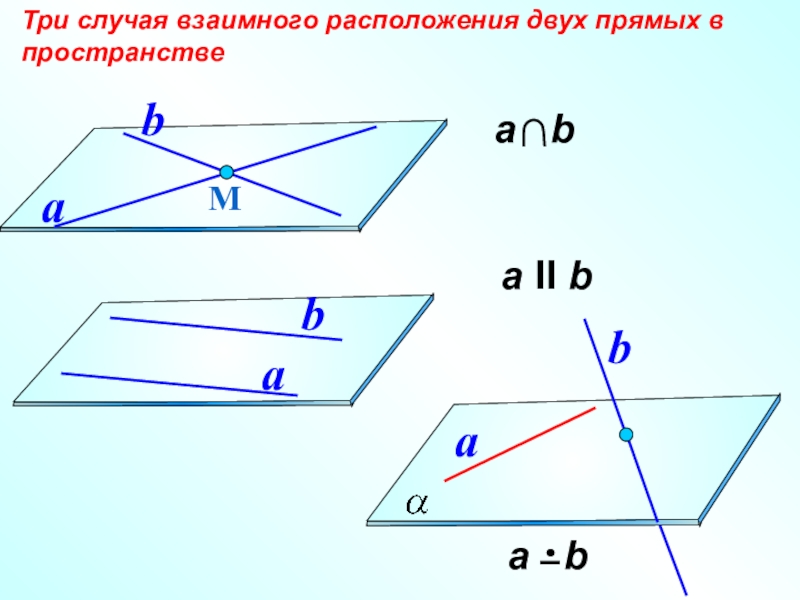
- 19. а II bТри случая взаимного расположения двух прямых в пространствеМababab
- 20. Слайд 20
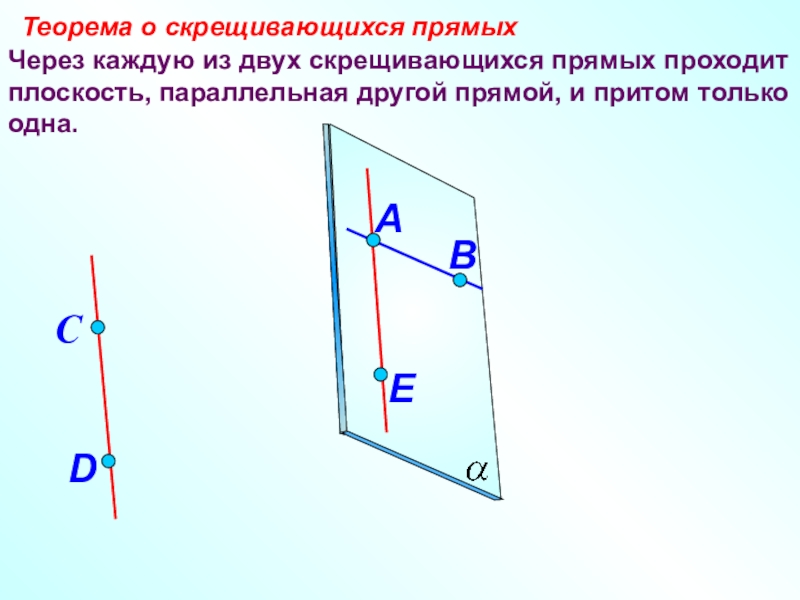
- 21. Через каждую из двух скрещивающихся прямых проходит
- 22. Теорема:Через каждую из двух скрещивающихся прямых проходит
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Задача №1.Построить плоскость α, проходящую через точку
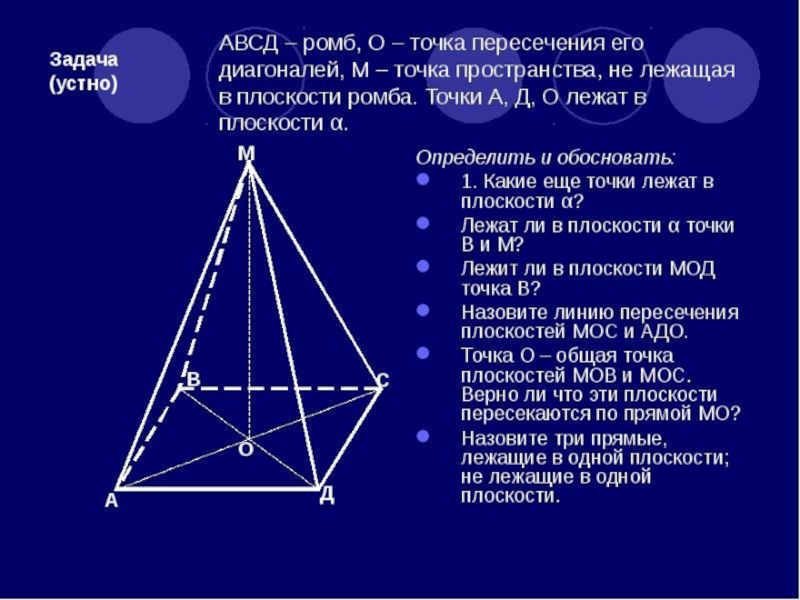
- 27. 2. Через вершину А ромба АВСD проведена
- 28. АDСВB1С1D1А13. Каково взаимное положение прямых1) AD1 и
- 29. АDСВB1С1D1А14. Докажите, что прямые 1) AD и
- 30. Задача№5.αabМNДано: a || bMN ∩ a = MОпределитьвзаимное расположениепрямых MN u b.Скрещивающиеся.
- 31. Задача №6АВСDMNPР1КДано: D (АВС),АМ =
- 32. АВСDMNPКДано: D (АВС),АМ = МD;
- 33. PABCDA1B1C1D1RMKQ Задача 8Назовите точки, лежащие в
- 34. Задача 9Назовите плоскости, в которых
- 35. №10. Дано; ABCD - параллелограмм, АВЕК- трапеция,
- 36. Угадай ребусы!
- 37. 1. Верно ли утверждение: если две прямые
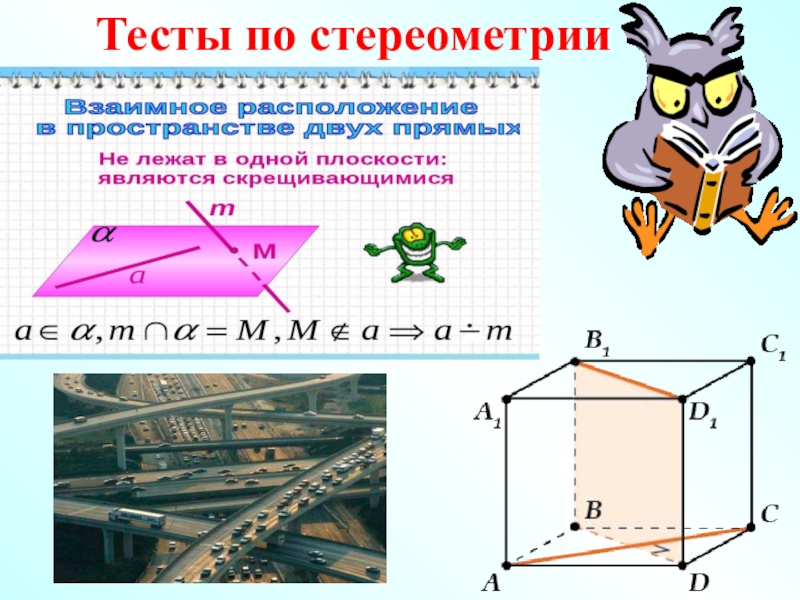
- 38. Тесты по стереометрии
- 39. Домашняя работа§2;п.7; №28; №34
- 40. Спасибо за урок!!!Что быстрее всего ? –
ЦЕЛИ УРОКА: Обучающая цель: Ввести понятие скрещивающихся прямых, доказать признак скрещивающихся прямых, теорему о проведении через одну из скрещивающихся прямых плоскости, параллельной другой прямой. Закрепить навык использования признака скрещивающихся прямых при решении задач. Развивающая цель: развивать
Слайд 1
Скрещивающиеся
прямые
ГБПОУ ВО «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПРОМЫШЛЕННО-ГУМАНИТАРНЫЙ КОЛЛЕДЖ»
Преподаватель:
Косян Анаит Георгиевна
Богучар
Слайд 2ЦЕЛИ УРОКА:
Обучающая цель:
Ввести понятие скрещивающихся прямых, доказать признак скрещивающихся
прямых, теорему о проведении через одну из скрещивающихся прямых плоскости, параллельной другой прямой. Закрепить навык использования признака скрещивающихся прямых при решении задач.
Развивающая цель:
развивать пространственное воображение студента,
геометрическое, логическое и алгоритмическое мышление; развивать мировоззрение учащихся, внимание, память, воображение, навыки самостоятельной работы.
Воспитательная цель:
показать связь геометрических построений с объектами окружающего мира, воспитывать трудолюбие, аккуратность, познавательную активность
интерес к математике и учебной деятельности в целом, культуру общения и активность.
Развивающая цель:
развивать пространственное воображение студента,
геометрическое, логическое и алгоритмическое мышление; развивать мировоззрение учащихся, внимание, память, воображение, навыки самостоятельной работы.
Воспитательная цель:
показать связь геометрических построений с объектами окружающего мира, воспитывать трудолюбие, аккуратность, познавательную активность
интерес к математике и учебной деятельности в целом, культуру общения и активность.
Слайд 31.Организация начала занятия.
2.Проверка домашнего задания.
3.Изучение нового материала.
4.Первичное закрепление знаний.
5. Контроль и
взаимопроверка знаний.
6.Подведение итогов, рефлексия.
7. Информация о домашнем задании.
6.Подведение итогов, рефлексия.
7. Информация о домашнем задании.
План урока
Слайд 4Вопросы для повторения
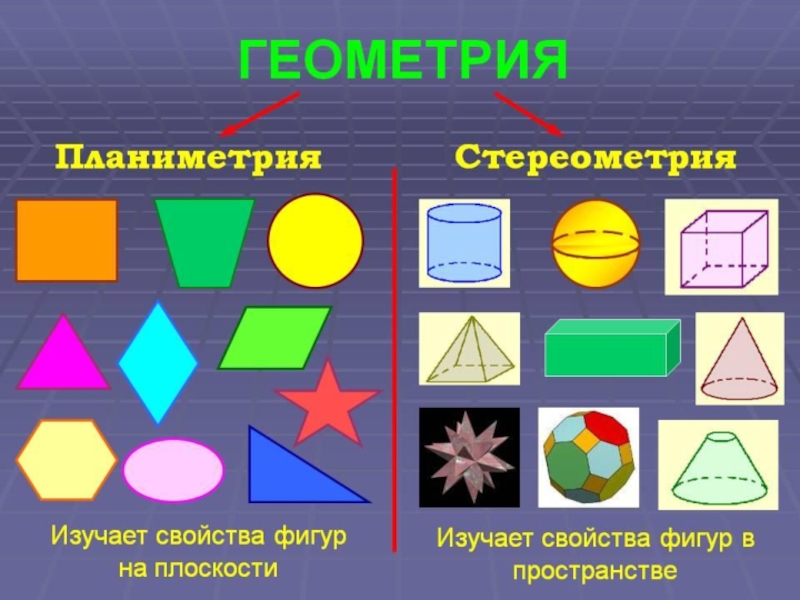
Что изучает стереометрия?
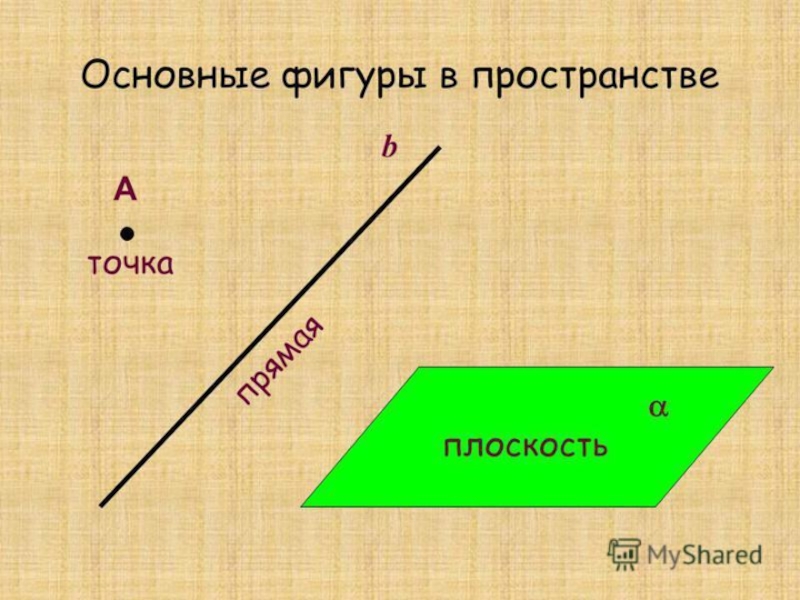
Основные понятия стереометрии.
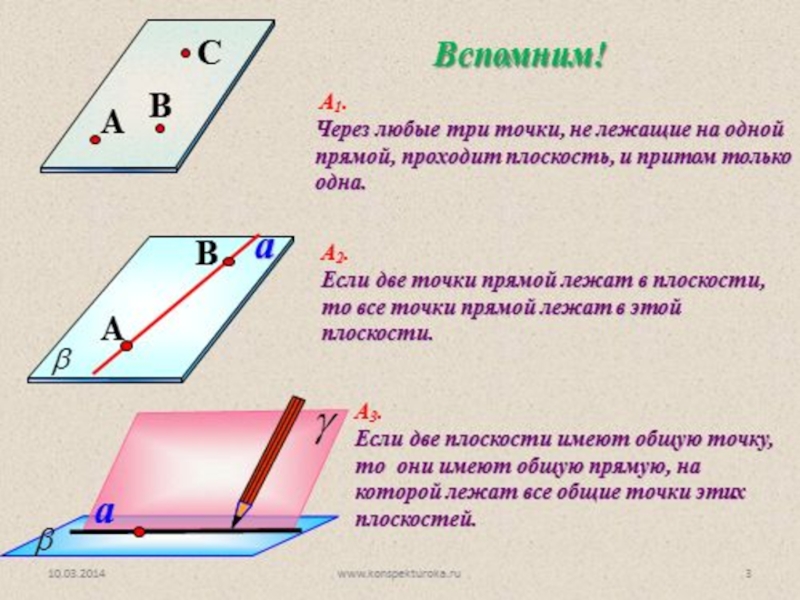
Аксиомы стереометрии.
Следствия из аксиом.
Какие прямые
называются параллельными?
Параллельность трех прямых.
Взаимное расположение прямой и плоскости.
Параллельность трех прямых.
Взаимное расположение прямой и плоскости.
Слайд 10
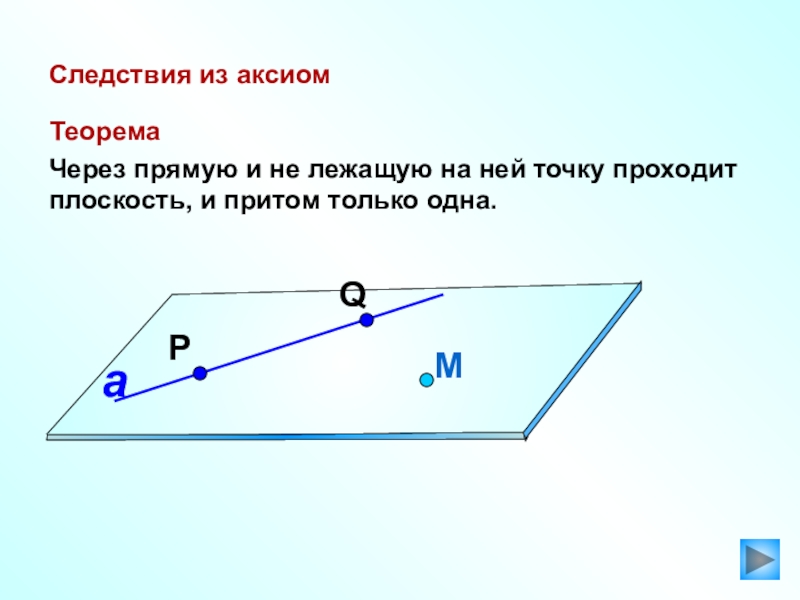
Следствия из аксиом
Теорема
Через прямую и не лежащую
на ней точку проходит плоскость, и притом только одна.
М
a
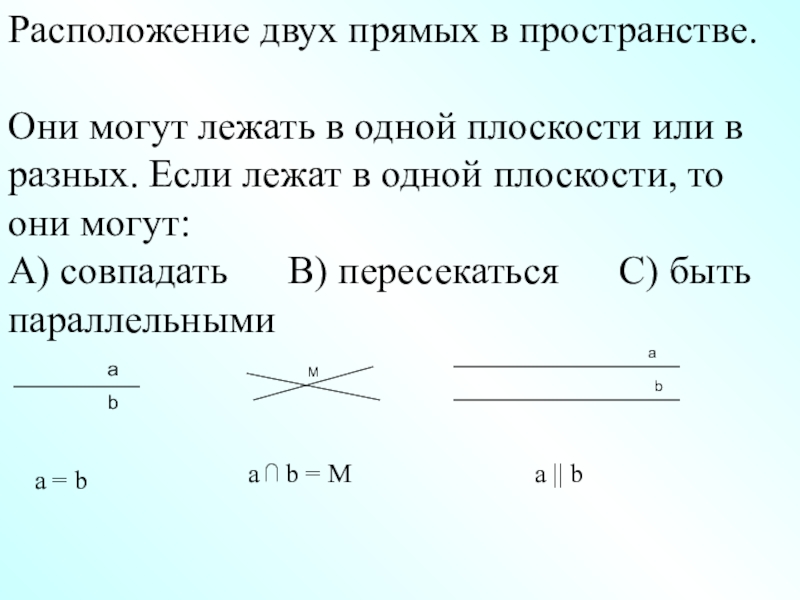
Слайд 12Расположение двух прямых в пространстве.
Они могут лежать в одной плоскости или
в разных. Если лежат в одной плоскости, то они могут:
А) совпадать В) пересекаться С) быть параллельными
А) совпадать В) пересекаться С) быть параллельными
a = b
b
a
M
a ⋂ b = M
a || b
a
b
Слайд 14
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi
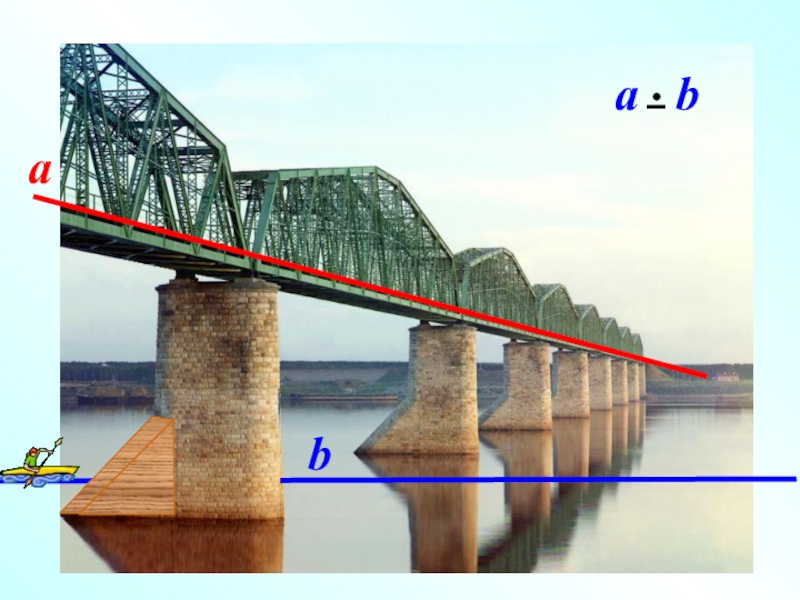
Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых
проходит по эстакаде, а другая под эстакадой.
Слайд 16Найдите на рисунке параллельные прямые.
Назовите параллельные прямые и плоскости.
Найдите скрещивающиеся прямые.
Слайд 17Если одна из двух прямых лежит в некоторой плоскости, а другая
прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Признак скрещивающихся прямых
D
В
А
C
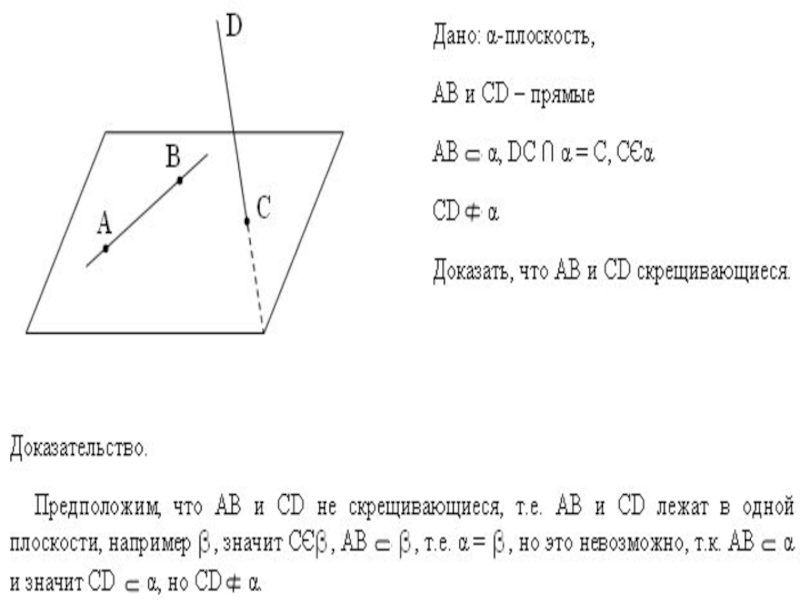
Слайд 18Признак скрещивающихся прямых.
Дано: АВ α, СD ∩ α =
С, С АВ.
a
b
Доказательство:
Допустим, что СD и АВ лежат в одной плоскости.
Пусть это будет плоскость β.
Доказать, что АВ
скрещивается с СD
А
В
С
D
α совпадает с β
Плоскости совпадают, чего быть не может, т.к. прямая СD
пересекает α. Плоскости, которой принадлежат АВ и СD не
существует и следовательно по определению скрещивающихся
прямых АВ скрещивается с СD. Ч.т.д.
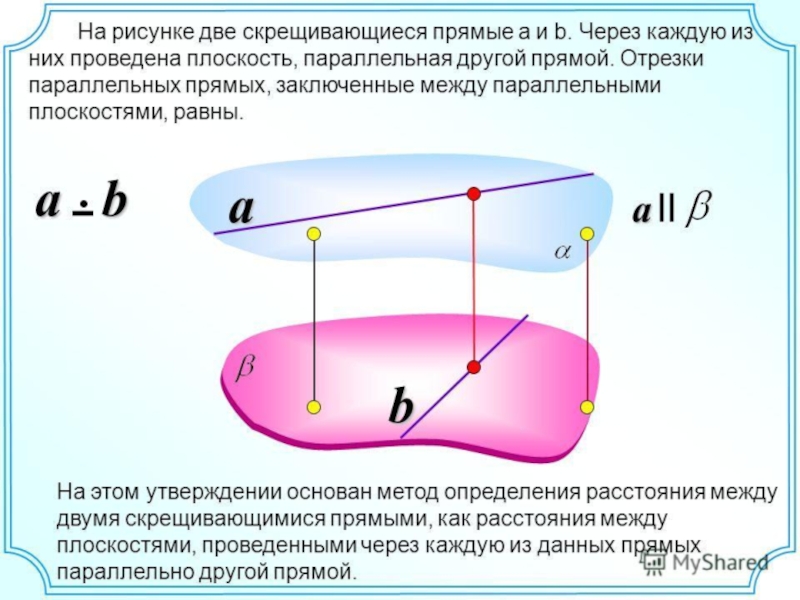
Слайд 21Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой,
и притом только одна.
Теорема о скрещивающихся прямых
D
С
B
A
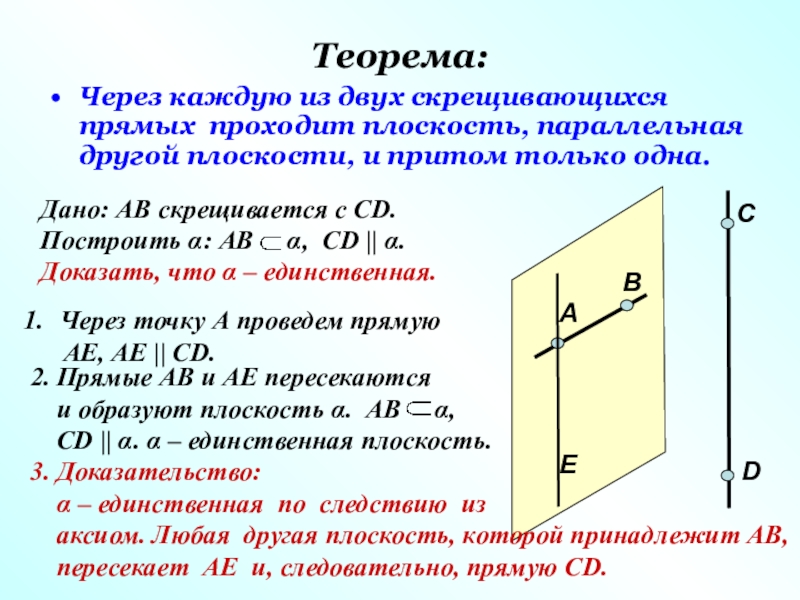
Слайд 22Теорема:
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости,
и притом только одна.
Дано: АВ скрещивается с СD.
Построить α: АВ α, СD || α.
А
В
C
D
Через точку А проведем прямую
АЕ, АЕ || СD.
Е
2. Прямые АВ и АЕ пересекаются
и образуют плоскость α. АВ α,
СD || α. α – единственная плоскость.
Доказать, что α – единственная.
3. Доказательство:
α – единственная по следствию из
аксиом. Любая другая плоскость, которой принадлежит АВ,
пересекает АЕ и, следовательно, прямую СD.
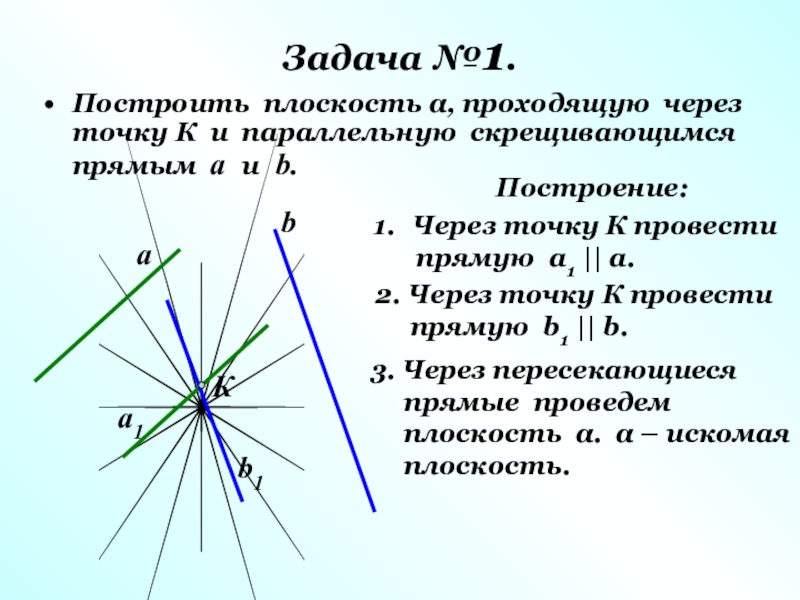
Слайд 26Задача №1.
Построить плоскость α, проходящую через точку К и параллельную скрещивающимся
прямым а и b.
Построение:
Через точку К провести
прямую а1 || а.
2. Через точку К провести
прямую b1 || b.
а
b
К
а1
b1
3. Через пересекающиеся
прямые проведем
плоскость α. α – искомая
плоскость.
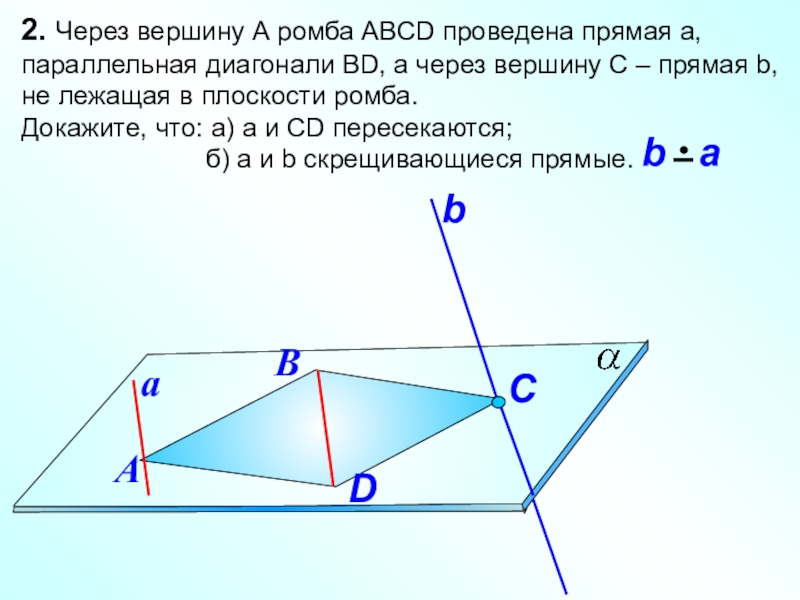
Слайд 27
2. Через вершину А ромба АВСD проведена прямая а, параллельная диагонали
ВD, а через вершину С – прямая b, не лежащая в плоскости ромба.
Докажите, что: а) а и СD пересекаются;
б) а и b скрещивающиеся прямые.
Докажите, что: а) а и СD пересекаются;
б) а и b скрещивающиеся прямые.
В
А
C
a
D
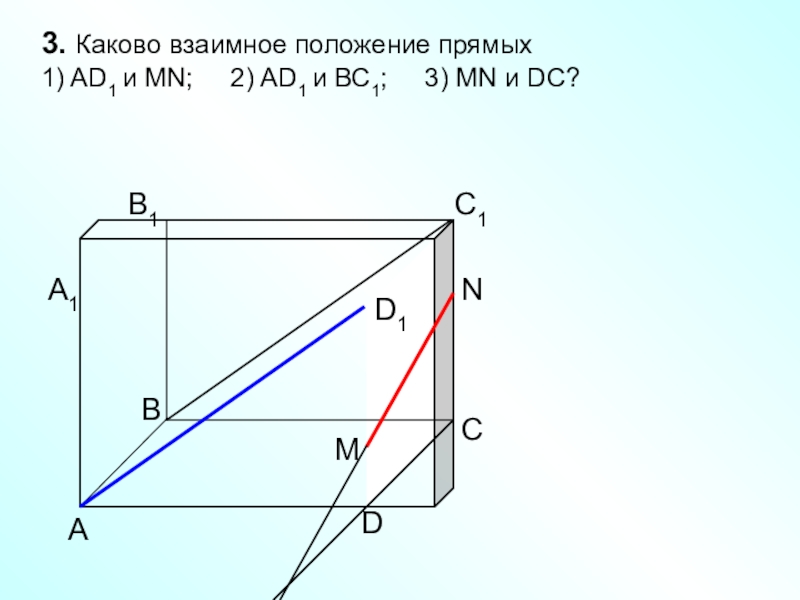
Слайд 29
А
D
С
В
B1
С1
D1
А1
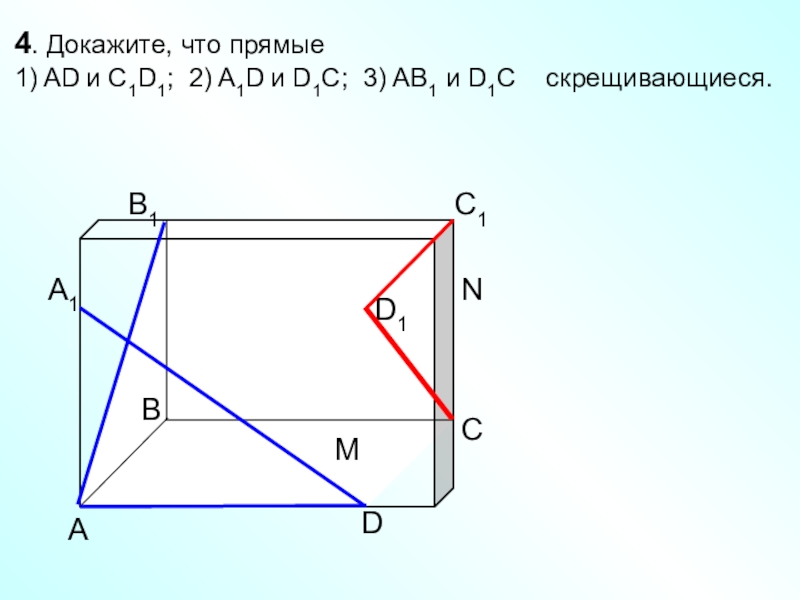
4. Докажите, что прямые
1) AD и C1D1; 2) A1D и
D1C; 3) AB1 и D1C скрещивающиеся.
N
M
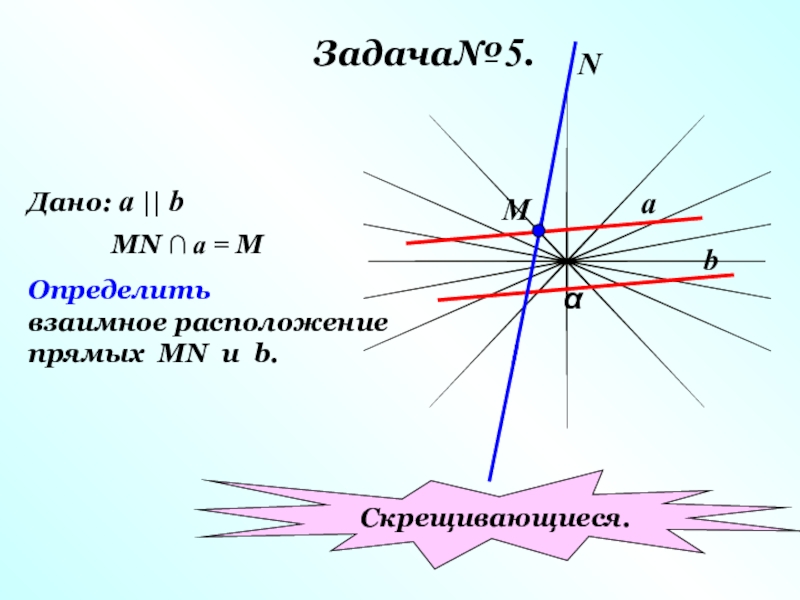
Слайд 30 Задача№5.
α
a
b
М
N
Дано: a || b
MN ∩ a = M
Определить
взаимное расположение
прямых MN
u b.
Скрещивающиеся.
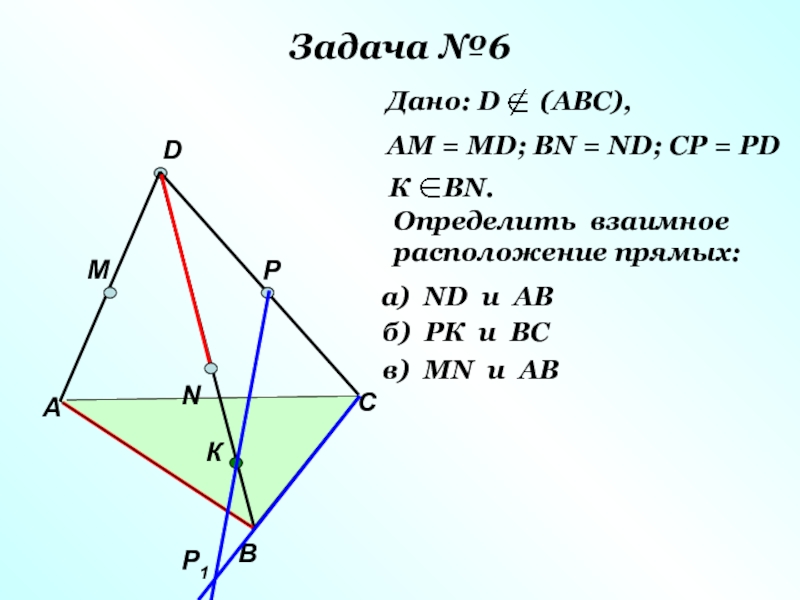
Слайд 31Задача №6
А
В
С
D
M
N
P
Р1
К
Дано: D (АВС),
АМ = МD; ВN = ND;
CP = PD
К ВN.
Определить взаимное
расположение прямых:
а) ND и AB
б) РК и ВС
в) МN и AB
Слайд 32
А
В
С
D
M
N
P
К
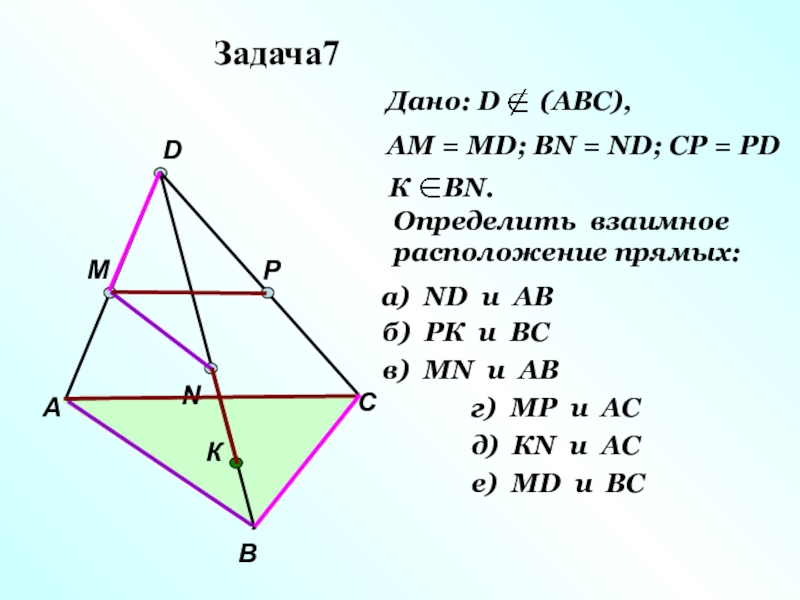
Дано: D (АВС),
АМ = МD; ВN = ND; CP
= PD
К ВN.
Определить взаимное
расположение прямых:
а) ND и AB
б) РК и ВС
в) МN и AB
г) МР и AС
д) КN и AС
е) МD и BС
Задача7
Слайд 33
P
A
B
C
D
A1
B1
C1
D1
R
M
K
Q
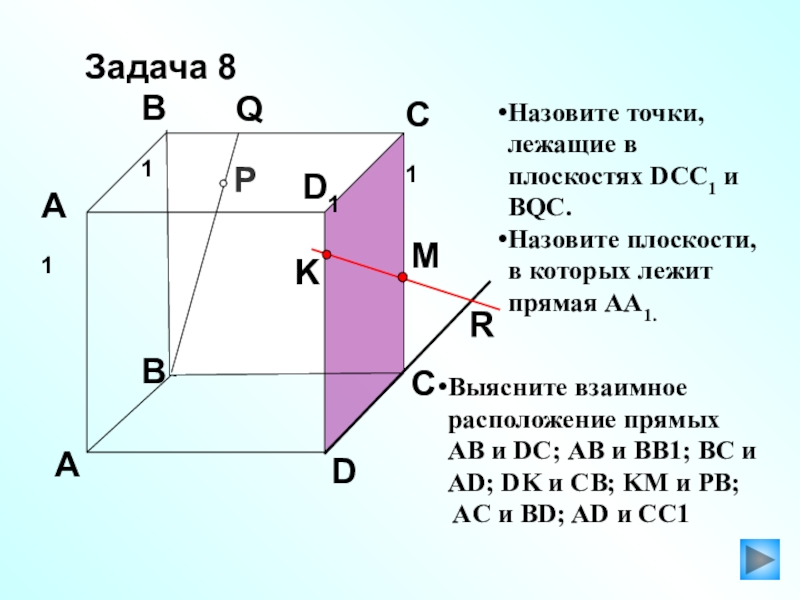
Задача 8
Назовите точки, лежащие в плоскостях DCC1 и BQC.
Назовите
плоскости, в которых лежит прямая АА1.
Выясните взаимное расположение прямых
AB и DС; AB и BB1; BC и AD; DK и CB; KM и PB;
AC и BD; AD и CC1
Слайд 34
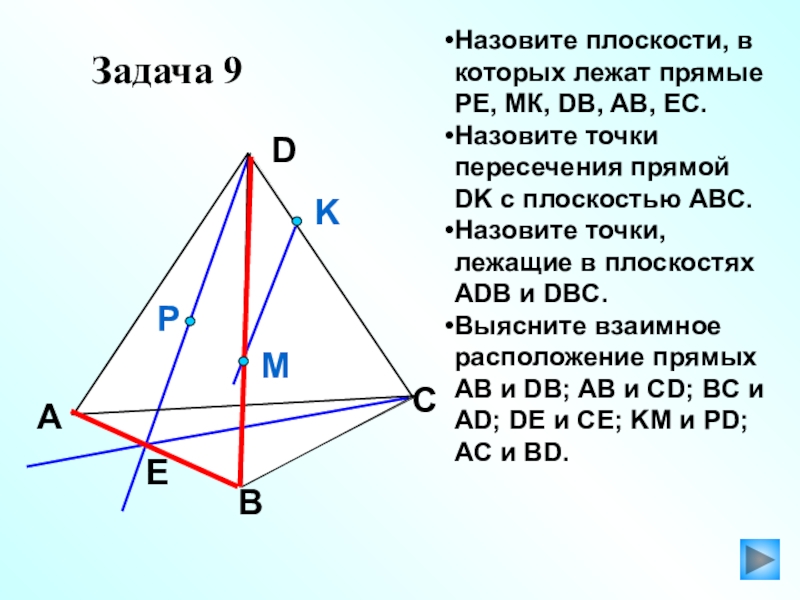
Задача 9
Назовите плоскости, в которых лежат прямые
РЕ, МК, DB,
AB, EC.
Назовите точки пересечения прямой DK с плоскостью АВС.
Назовите точки, лежащие в плоскостях АDB и DBC.
Выясните взаимное расположение прямых
AB и DB; AB и CD; BC и AD; DE и CE; KM и PD; AC и BD.
Назовите точки пересечения прямой DK с плоскостью АВС.
Назовите точки, лежащие в плоскостях АDB и DBC.
Выясните взаимное расположение прямых
AB и DB; AB и CD; BC и AD; DE и CE; KM и PD; AC и BD.
P
E
A
B
C
D
M
K
Слайд 35
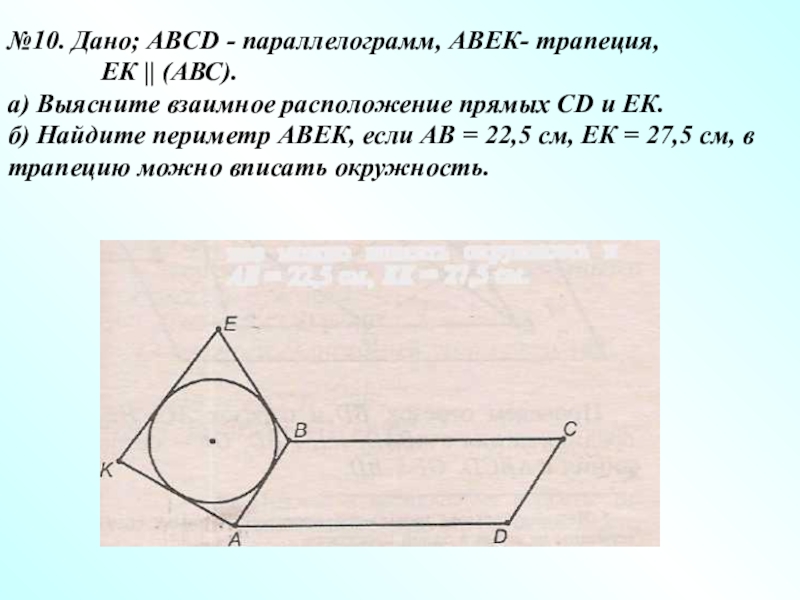
№10. Дано; ABCD - параллелограмм, АВЕК- трапеция,
ЕК || (АВС).
а) Выясните взаимное расположение прямых CD и ЕК.
б) Найдите периметр АВЕК, если АВ = 22,5 см, ЕК = 27,5 см, в трапецию можно вписать окружность.
а) Выясните взаимное расположение прямых CD и ЕК.
б) Найдите периметр АВЕК, если АВ = 22,5 см, ЕК = 27,5 см, в трапецию можно вписать окружность.
Слайд 371. Верно ли утверждение: если две прямые не имеют общих точек,
то они параллельны?
2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) пересекаться; б) быть скрещивающимися?
3. Могут ли скрещивающиеся прямые а и в быть параллельными прямой с ? Ответ обоснуйте.
4. Прямая а скрещивается с прямой в, а прямая в скрещивается с прямой с . Следует ли из этого, что прямые а и с скрещивающиеся?
5. Каково должно быть взаимное расположение трех прямых, чтобы можно было провести плоскость, содержащую все прямые?
6. Можно ли провести прямую, пересекающую каждую из трех скрещивающихся прямых?
7. Даны две пересекающиеся плоскости. В одной из них лежит прямая а, в другой плоскости - прямая в. Лежат ли прямые а и в в одной плоскости, если известно, что они пересекают линию пересечения плоскостей : а) в одной точке; б) в разных точках.
8. Даны две параллельные плоскости . В одной плоскости лежит прямая а, в другой плоскости - прямая в. Каковы взаимные случаи расположения прямых а и в?
2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) пересекаться; б) быть скрещивающимися?
3. Могут ли скрещивающиеся прямые а и в быть параллельными прямой с ? Ответ обоснуйте.
4. Прямая а скрещивается с прямой в, а прямая в скрещивается с прямой с . Следует ли из этого, что прямые а и с скрещивающиеся?
5. Каково должно быть взаимное расположение трех прямых, чтобы можно было провести плоскость, содержащую все прямые?
6. Можно ли провести прямую, пересекающую каждую из трех скрещивающихся прямых?
7. Даны две пересекающиеся плоскости. В одной из них лежит прямая а, в другой плоскости - прямая в. Лежат ли прямые а и в в одной плоскости, если известно, что они пересекают линию пересечения плоскостей : а) в одной точке; б) в разных точках.
8. Даны две параллельные плоскости . В одной плоскости лежит прямая а, в другой плоскости - прямая в. Каковы взаимные случаи расположения прямых а и в?
Ответить на вопросы
Слайд 40Спасибо за урок!!!
Что быстрее всего ? – Ум.
Что мудрее всего ?
– Время.
Что приятнее всего ? –
Достичь желаемого. Фалес Милетский
Что приятнее всего ? –
Достичь желаемого. Фалес Милетский
