- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Решение олимпиадных задач для 5-6 классов
Содержание
- 1. Презентация по математике на тему Решение олимпиадных задач для 5-6 классов
- 2. Эпиграф«Весь смысл жизни заключается в бесконечном завоевании неизвестного, в вечном усилии познать больше».Э. Золя
- 3. Магический квадрат Задача В
- 4. Задачи по арифметикеЗадача Замените значки * в
- 5. При решении задач, в которых используются свойства
- 6. Задача Света выполнила действия:
- 7. Математические ребусыЗадача Решите ребус999998887663311
- 8. Задачи на разрезание и складывание фигур Задача
- 9. Задачи, решаемые с концаЗадача Группа туристов отправилась
- 10. Задачи типа "Кто есть кто?" Задача. В
- 11. Принцип ДирихлеЗадача В классе 22 ученика. Можно
- 12. Принцип ДирихлеЗадача В классе 22 ученика. Можно
- 13. Задачи на переливаниеЗадача Как с помощью 7-литрового
- 14.
Эпиграф«Весь смысл жизни заключается в бесконечном завоевании неизвестного, в вечном усилии познать больше».Э. Золя
Слайд 2Эпиграф
«Весь смысл жизни заключается в бесконечном завоевании неизвестного, в вечном усилии
познать больше».
Э. Золя
Э. Золя
Слайд 3 Магический квадрат
Задача В клетках квадрата 3 x
3 были записаны натуральные числа так, чтобы они образовывали магический квадрат. Некоторые числа стерли, восстановите квадрат.
12
27
3
Слайд 4Задачи по арифметике
Задача Замените значки * в выражении 13*11*9*7*5*3*1
= 1 на знаки + и – так, чтобы получилось верное равенство.
Ответ:
13 + 11 – 9 – 7 – 5 – 3 + 1 = 1;
13 – 11 + 9 – 7 – 5 + 3 – 1 = 1;
13 – 11 – 9 + 7 + 5 – 3 – 1 = 1.
Ответ:
13 + 11 – 9 – 7 – 5 – 3 + 1 = 1;
13 – 11 + 9 – 7 – 5 + 3 – 1 = 1;
13 – 11 – 9 + 7 + 5 – 3 – 1 = 1.
Слайд 5При решении задач, в которых используются свойства четности, важно помнить следующие
правила:
1. Сумма и разность двух нечетных чисел является четным числом.
2. Сумма и разность двух четных чисел является четным числом.
3. Сумма и разность двух чисел, одно из которых четное, а другое нечетное, является нечетным числом.
4. Произведение двух нечетных чисел является нечетным числом.
5. Произведение двух чисел, из которых одно четное, является четным числом.
Слайд 6Задача Света выполнила действия: 1997 ∙ 1999 ∙ 2001
– 1998 ∙ 2000.
Какова последняя цифра ответа?
Ответ:
Произведение 1997 ∙ 1999 ∙ 2001 оканчивается цифрой 3, поскольку 7 ∙ 9 ∙ 1 = 63.
Произведение 1998 ∙ 2000 оканчивается 0
Следовательно результат оканчивается цифрой 3.
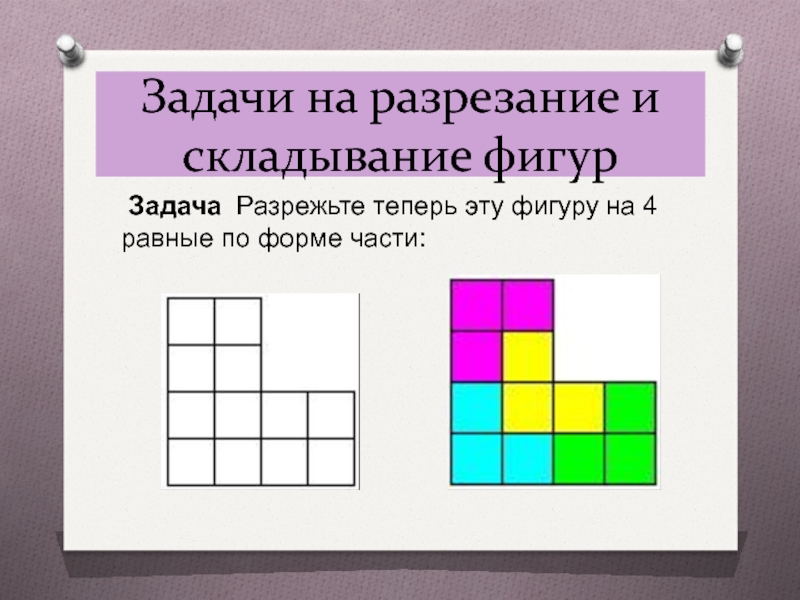
Слайд 8Задачи на разрезание и складывание фигур
Задача Разрежьте теперь эту фигуру
на 4 равные по форме части:
Слайд 9Задачи, решаемые с конца
Задача Группа туристов отправилась в поход. В первый
день они прошли 1/3 пути, в второй - 1/3 остатка, в третий - 1/3 нового остатка. В результате им осталось пройти 32 км. Сколько километров был маршрут туристов?
Решение:
32 : 2/3 = 48 (км) - последний остаток
48 : 2/3 = 72 (км) - 2/3 всего маршрута туристов
72 : 2/3 = 108 (км)
Ответ: 108 км
Решение:
32 : 2/3 = 48 (км) - последний остаток
48 : 2/3 = 72 (км) - 2/3 всего маршрута туристов
72 : 2/3 = 108 (км)
Ответ: 108 км
Слайд 10Задачи типа "Кто есть кто?"
Задача. В кругу сидят Иванов, Петров,
Марков и Карпов. Их имена Андрей, Сергей, Тимофей и Алексей. Известно, что:
1. Иванов не Алексей и не Андрей.
2. Карпов не Сергей и не Алексей.
3. Сергей сидит между Марковым и Тимофеем.
4. Петров сидит между Карповым и Андреем.
Назовите имя и фамилию каждого.
Решение:
1. Иванов не Алексей и не Андрей.
2. Карпов не Сергей и не Алексей.
3. Сергей сидит между Марковым и Тимофеем.
4. Петров сидит между Карповым и Андреем.
Назовите имя и фамилию каждого.
Решение:
-
-
-
-
-
-
-
-
+
-
+
-
-
+
-
+
Слайд 11Принцип Дирихле
Задача В классе 22 ученика. Можно ли утверждать, что среди
них найдутся хотя бы два ученика, фамилии которых начинаются с одной буквы.
Решение: Пусть «зайцы» - это ученики, «клетки» - буквы. В алфавите 33 буквы. Фамилии не могут начинаться с мягкого и твердого знаков, значит, остается 31 буква. Получается, что «клеток» (31) больше, чем «зайцев» (22). Принцип Дирихле нельзя применить. Поменяем «клетки» и «зайцев». По принципу Дирихле каждый ученик имеет свою собственную букву. Ответ на вопрос задачи – «нет».
Решение: Пусть «зайцы» - это ученики, «клетки» - буквы. В алфавите 33 буквы. Фамилии не могут начинаться с мягкого и твердого знаков, значит, остается 31 буква. Получается, что «клеток» (31) больше, чем «зайцев» (22). Принцип Дирихле нельзя применить. Поменяем «клетки» и «зайцев». По принципу Дирихле каждый ученик имеет свою собственную букву. Ответ на вопрос задачи – «нет».
Слайд 12Принцип Дирихле
Задача В классе 22 ученика. Можно ли утверждать, что среди
них найдутся хотя бы два ученика, фамилии которых начинаются с одной буквы.
Решение: Пусть «зайцы» - это ученики, «клетки» - буквы. В алфавите 33 буквы. Фамилии не могут начинаться с мягкого и твердого знаков, значит, остается 31 буква. Получается, что «клеток» (31) больше, чем «зайцев» (22). Принцип Дирихле нельзя применить. Поменяем «клетки» и «зайцев». По принципу Дирихле найдутся две буквы, с которых может начинаться фамилия какого-нибудь ученика, следовательно, каждый ученик имеет свою собственную букву.
Ответ на вопрос задачи – «нет».
Решение: Пусть «зайцы» - это ученики, «клетки» - буквы. В алфавите 33 буквы. Фамилии не могут начинаться с мягкого и твердого знаков, значит, остается 31 буква. Получается, что «клеток» (31) больше, чем «зайцев» (22). Принцип Дирихле нельзя применить. Поменяем «клетки» и «зайцев». По принципу Дирихле найдутся две буквы, с которых может начинаться фамилия какого-нибудь ученика, следовательно, каждый ученик имеет свою собственную букву.
Ответ на вопрос задачи – «нет».
Слайд 13Задачи на переливание
Задача Как с помощью 7-литрового ведра и 3-литровой банки
отмерить 5 л воды?
Решение:
Решение:
