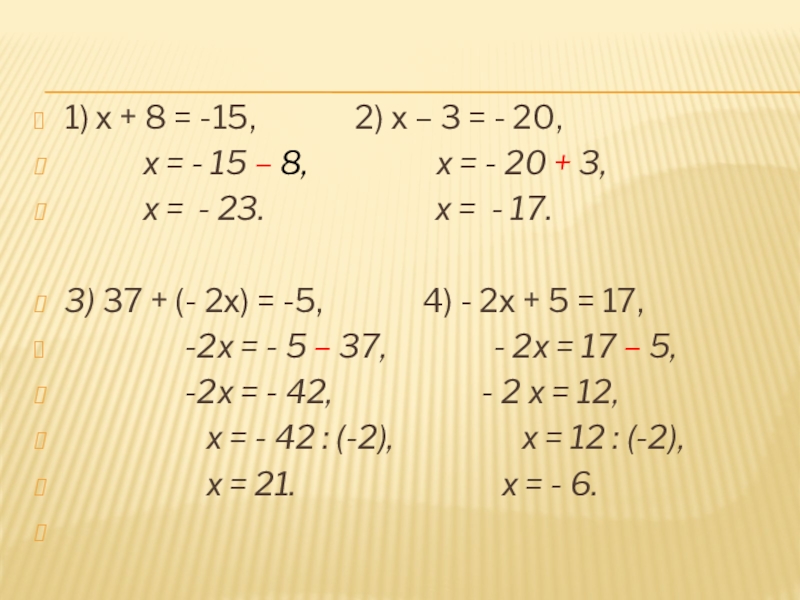- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Решение уравнений 6 класс
Содержание
- 1. Презентация по математике на тему Решение уравнений 6 класс
- 2. ЗАДАЧИ УРОКА: Образовательные:- начать формирование умений учащихся
- 3. ПОВТОРЕНИЕ. Устно:Повторим знаки при раскрытии скобок и
- 4. ВЫЧИСЛИТЕ И ПОКАЖИТЕ ОТВЕТ ОБЕИМИ РУКАМИ В
- 5. ПРИВЕДИТЕ ПОДОБНЫЕ СЛАГАЕМЫЕ: а) 9,5m +
- 6. РАСКРЫТЬ СКОБКИ И ПРИВЕСТИ ПОДОБНЫЕ СЛАГАЕМЫЕ:Письменно: а)
- 7. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА. Решите уравнения и покажите
- 8. 1) х + 8 = -15,
- 9. ВЫВОД:Слагаемые без переменной перешли из левой части уравнения в правую с ________________ знаком.
- 10. 5) 6х = 3х + 9,
- 11. ПРАВИЛО:Корни уравнения не изменятся, если какое-нибудь слагаемое
- 12. ЗАКРЕПЛЕНИЕ. Соберите в левой части уравнения все
- 13. Решить уравнения: № 1300а) 6х – 12
- 14. Решите уравнение и составьте алгоритм решения уравнения:
- 15. ПРОВЕРИМРешение:
- 16. Во всех рассмотренных примерах мы приводили данные
- 17. Решаем уравнения по алгоритму:б) 2(3х –
- 18. № 1305 ЗАДАЧА. В первом бидоне в
- 19. КРАТКАЯ ЗАПИСЬ:
- 20. РЕШЕНИЕ: Пусть х л. молока было во
- 21. № 1322 Докажите, что при любом значении
- 22. ЗАПИШЕМ И РЕШИМ УРАВНЕНИЕ:35у -10 - 35у
- 23. ПОВТОРЕНИЕ. Повторим правило и алгоритм решения уравнений.Как
- 24. № 1300Попробуйте решить уравнения устно:
- 25. ИТОГ УРОКА. Проанализируйте, пожалуйста, каждый
- 26. ДОМАШНЕЕ ЗАДАНИЕ:п. 42 (выучить правило и алгоритм),
ЗАДАЧИ УРОКА: Образовательные:- начать формирование умений учащихся решать уравнения способом переноса слагаемых из одной части в другую;- познакомить с понятием линейное уравнение;- закрепить умение преобразования выражений в ходе решения уравнений;- продолжить формирование умений решать задачи составлением
Слайд 1РЕШЕНИЕ УРАВНЕНИЙ. 6 КЛАСС. УРОК ОЗНАКОМЛЕНИЯ С НОВЫМ МАТЕРИАЛОМ.
Цель урока:
Научить учащихся решать уравнения способом переноса слагаемых из одной части в другую.
Познакомить с понятием линейного уравнения.
Слайд 2ЗАДАЧИ УРОКА:
Образовательные:
- начать формирование умений учащихся решать уравнения способом переноса слагаемых
из одной части в другую;
- познакомить с понятием линейное уравнение;
- закрепить умение преобразования выражений в ходе решения уравнений;
- продолжить формирование умений решать задачи составлением уравнений;
Развивающие:
- развитие памяти, внимания учащихся;
- развитие умений преодолевать трудности при решении уравнений и задач;
- развитие познавательного интереса учащихся;
- развитие логического мышления учащихся.
Воспитательные:
- воспитание активности и аккуратности учащихся;
- воспитание настойчивости в достижении цели;
- привитие учащимся навыков самостоятельной работы.
- познакомить с понятием линейное уравнение;
- закрепить умение преобразования выражений в ходе решения уравнений;
- продолжить формирование умений решать задачи составлением уравнений;
Развивающие:
- развитие памяти, внимания учащихся;
- развитие умений преодолевать трудности при решении уравнений и задач;
- развитие познавательного интереса учащихся;
- развитие логического мышления учащихся.
Воспитательные:
- воспитание активности и аккуратности учащихся;
- воспитание настойчивости в достижении цели;
- привитие учащимся навыков самостоятельной работы.
Слайд 3ПОВТОРЕНИЕ.
Устно:
Повторим знаки при раскрытии скобок и при умножении и делении чисел
с разными знаками:
- (+) = (-) ∙ (+) = (-) : (+) =
- (-) = (-) ∙ (-) = (-) : (-) =
+ (-) = (+) ∙ (-) = (+) : (-) =
+ (+) = (+) ∙ (+) = (+) : (+) =
- (+) = (-) ∙ (+) = (-) : (+) =
- (-) = (-) ∙ (-) = (-) : (-) =
+ (-) = (+) ∙ (-) = (+) : (-) =
+ (+) = (+) ∙ (+) = (+) : (+) =
Слайд 4ВЫЧИСЛИТЕ И ПОКАЖИТЕ ОТВЕТ ОБЕИМИ РУКАМИ В ЗЕРКАЛЬНОМ ОТРАЖЕНИИ:
8 – 70
= - 19 + 19 =
0 - 19 = 78 : (-3) =
- 81 : 3 = -27 – 13 =
- 26 ∙ (-2) = - 20 + 6 =
0 - 19 = 78 : (-3) =
- 81 : 3 = -27 – 13 =
- 26 ∙ (-2) = - 20 + 6 =
Слайд 5ПРИВЕДИТЕ ПОДОБНЫЕ СЛАГАЕМЫЕ:
а) 9,5m + 3m =
б) 6в
– в =
в) 1,2у + 3,6у – 0,7у =
г) – 4х – х + 3 =
д) 7х – 6у – 2х + 8у =
в) 1,2у + 3,6у – 0,7у =
г) – 4х – х + 3 =
д) 7х – 6у – 2х + 8у =
Слайд 6РАСКРЫТЬ СКОБКИ И ПРИВЕСТИ ПОДОБНЫЕ СЛАГАЕМЫЕ:
Письменно:
а) 5 ∙ (а –
2) – 4 ∙ (2,5 – а) =
б) 4(х – 1,7) – 3(1,5 – х) =
в) - 2,4(2у – 3) + 3(2,1у – 1) =
б) 4(х – 1,7) – 3(1,5 – х) =
в) - 2,4(2у – 3) + 3(2,1у – 1) =
Слайд 7ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА.
Решите уравнения и покажите ответ носиком:
1) х + 8 = -15
2) х – 3 = - 20
3) 37 + (- 2х) = -5
4) - 2х + 5 = 17
2) х – 3 = - 20
3) 37 + (- 2х) = -5
4) - 2х + 5 = 17
Слайд 8
1) х + 8 = -15,
2) х – 3 = - 20,
х = - 15 – 8, х = - 20 + 3,
х = - 23. х = - 17.
3) 37 + (- 2х) = -5, 4) - 2х + 5 = 17,
-2х = - 5 – 37, - 2х = 17 – 5,
-2х = - 42, - 2 х = 12,
х = - 42 : (-2), х = 12 : (-2),
х = 21. х = - 6.
х = - 15 – 8, х = - 20 + 3,
х = - 23. х = - 17.
3) 37 + (- 2х) = -5, 4) - 2х + 5 = 17,
-2х = - 5 – 37, - 2х = 17 – 5,
-2х = - 42, - 2 х = 12,
х = - 42 : (-2), х = 12 : (-2),
х = 21. х = - 6.
Слайд 9ВЫВОД:
Слагаемые без переменной перешли из левой части уравнения в правую с
________________ знаком.
Слайд 10
5) 6х = 3х + 9,
6) 5х = 2х + 6,
6х 3х = 9. 5х 2х = 6.
7) 3х + 12 = х, 8) 3х – 19 = 4х – 10,
3х х = 12. 3х 4х = - 10 3х.
Вывод:
Слагаемые без переменной перешли из левой части уравнения в правую и, наоборот, слагаемые с переменной - из правой в левую с ___________________ знаком.
6х 3х = 9. 5х 2х = 6.
7) 3х + 12 = х, 8) 3х – 19 = 4х – 10,
3х х = 12. 3х 4х = - 10 3х.
Вывод:
Слагаемые без переменной перешли из левой части уравнения в правую и, наоборот, слагаемые с переменной - из правой в левую с ___________________ знаком.
Слайд 11ПРАВИЛО:
Корни уравнения не изменятся, если какое-нибудь слагаемое перенести из одной части
уравнения в другую, изменив при этом его знак.
(Три раза прочитайте правило (постарайтесь запомнить), а теперь вслух хором.)
(Три раза прочитайте правило (постарайтесь запомнить), а теперь вслух хором.)
Слайд 12ЗАКРЕПЛЕНИЕ.
Соберите в левой части уравнения все слагаемые, содержащие неизвестное, а в
правой части – слагаемые, не содержащие неизвестное:
№ 1298 а) 8х + 5,9 = 7х + 20 б) 6х – 8 = - 5х – 1,6
№ 1299 а) 15у – 8 = - 6у + 4,6 б) -16z + 1,7 = 2z – 1
№ 1298 а) 8х + 5,9 = 7х + 20 б) 6х – 8 = - 5х – 1,6
№ 1299 а) 15у – 8 = - 6у + 4,6 б) -16z + 1,7 = 2z – 1
Слайд 13
Решить уравнения: № 1300
а) 6х – 12 = 5х + 4
б) – 9а + 8 = - 10а – 2
Самостоятельно:
в) 7m + 1 = 8m + 9
г) - 12n – 3 = 11n – 3
Слайд 15ПРОВЕРИМ
Решение: Раскрыть
скобки;
21х – 7 = 5х – 15 Перенести слагаемые из одной части уравнения в другую, изменив при этом его знак;
21х – 5х = - 15 + 7 Привести подобные слагаемые;
16х = - 8 Найти корень уравнения.
х = - 8 : 16
х = - 0,5
Ответ: - 0,5.
21х – 7 = 5х – 15 Перенести слагаемые из одной части уравнения в другую, изменив при этом его знак;
21х – 5х = - 15 + 7 Привести подобные слагаемые;
16х = - 8 Найти корень уравнения.
х = - 8 : 16
х = - 0,5
Ответ: - 0,5.
Слайд 16Во всех рассмотренных примерах мы приводили данные уравнения к виду ах
= в, где а ≠ 0.
Уравнение вида ах = в, где а ≠ 0 называют линейным уравнением с одним неизвестным.
Уравнение вида ах = в, где а ≠ 0 называют линейным уравнением с одним неизвестным.
Слайд 17
Решаем уравнения по алгоритму:
б) 2(3х – 8) = - 13
+ 3(4х – 9)
Самостоятельно:
в) 9 – (4 + х) = 5(х + 1)
г) 3х + 2(2х – 3) = 8 – 7(х – 2)
Самостоятельно:
в) 9 – (4 + х) = 5(х + 1)
г) 3х + 2(2х – 3) = 8 – 7(х – 2)
Слайд 18№ 1305 ЗАДАЧА.
В первом бидоне в 3 раза больше молока, чем
во втором. Если из первого перелить 20л во второй, то молока в бидонах будет поровну. Сколько молока в каждом бидоне?
Слайд 20РЕШЕНИЕ:
Пусть х л. молока было во втором бидоне, тогда 3х л.
молока было в первом бидоне. После переливания в первом бидоне останется (3х – 20)л. молока, а во втором бидоне будет (х + 20)л. молока. По условию задачи молока в бидонах будет поровну. Составим уравнение:
3х – 20 = х + 20
3х – х = 20 + 20
2х = 40
х = 20
Значит, 20 л. молока было во втором бидоне, а в первом бидоне 3 ∙ 20 = 60 (л.) молока.
Ответ: 60 л., 20 л.
3х – 20 = х + 20
3х – х = 20 + 20
2х = 40
х = 20
Значит, 20 л. молока было во втором бидоне, а в первом бидоне 3 ∙ 20 = 60 (л.) молока.
Ответ: 60 л., 20 л.
Слайд 21№ 1322
Докажите, что при любом значении буквы значение выражения:
а) 5 ∙
(7у – 2) – 7 ∙ (5у + 2) равно – 24;
Слайд 22ЗАПИШЕМ И РЕШИМ УРАВНЕНИЕ:
35у -10 - 35у -14 = - 24
24 = - 24 - верно
Вывод:
Самостоятельно:
б) 4 ∙ (8а + 3) – 8 ∙ (4а – 3) равно 36.
Вывод:
Самостоятельно:
б) 4 ∙ (8а + 3) – 8 ∙ (4а – 3) равно 36.
Слайд 23ПОВТОРЕНИЕ.
Повторим правило и алгоритм решения уравнений.
Как называются уравнения, которые решали сегодня
на уроке?
Какое уравнение называют линейным?
Какое уравнение называют линейным?
Слайд 24№ 1300
Попробуйте решить уравнения устно:
д) 4 + 25у = 6 + 24у
е) 11 – 5z = 12 – 6z
ж) 4k + 7 = - 3 + 5k
з) 6 – 2с = 8 – 3с.
е) 11 – 5z = 12 – 6z
ж) 4k + 7 = - 3 + 5k
з) 6 – 2с = 8 – 3с.
Слайд 25ИТОГ УРОКА.
Проанализируйте, пожалуйста, каждый свою работу и работу товарищей
на уроке.
- Что новое узнали?
- Что было легко, и что ещё вызывает трудности (какой этап в алгоритме самый трудный и непонятный)?
- Над чем ещё нужно работать?
- Кто может уверенно сказать, что понял как надо решать уравнения?
- Кто вообще ничего не понял?
- Что новое узнали?
- Что было легко, и что ещё вызывает трудности (какой этап в алгоритме самый трудный и непонятный)?
- Над чем ещё нужно работать?
- Кто может уверенно сказать, что понял как надо решать уравнения?
- Кто вообще ничего не понял?
Слайд 26ДОМАШНЕЕ ЗАДАНИЕ:
п. 42 (выучить правило и алгоритм),
№
1325 (а, б), 1326 (а, в), 1330 (задача аналогичная задаче № 1305).