XVII веке.
Долгое время комбинаторика лежала вне основного русла развития математики. Положение дел резко изменилось после появления быстродействующих вычислительных машин.
В настоящее время комбинаторные методы применяются в теории случайных процессов, статистике, математическом программировании, вычислительной математике и др.»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Простейшие задачи комбинаторики (5-6 класс)
Содержание
- 1. Презентация по математике на тему: Простейшие задачи комбинаторики (5-6 класс)
- 2. Во взрослой жизни человеку часто приходится стоять
- 3. В науке
- 4. Определите, какие из задач являются комбинаторными.№4. Сколькими
- 5. Простейшие задачи комбинаторики.
- 6. Способ рассуждений – метод непосредственного перебора возможных вариантов.
- 7. Пример №1. Из группы
- 8. ГСФАГАГ, АС, АФ.Пары, в которые входит Антонов:СПары,
- 9. Пример №2. Три друга – Антон, Борис
- 10. Решение: Для записи трехзначного числа используем 3
- 11. Слайд 11
- 12. Слайд 12
- 13. Меню кафе «Минутка»Первое блюдоБорщРассольникВторое блюдо1 Гуляш2. Котлеты3. Сосиски4. ПельмениКафе «Минутка»
- 14. Рассольник, гуляш.Рассольник, котлеты.Рассольник, сосиски.Рассольник, пельмени.Борщ, гуляш.Борщ, котлеты.Борщ, сосиски.Борщ, пельмени.
- 15. Решение задачи с использованием таблицы.
- 16. I блюдоII блюдо№1№2№3№4№5№6№7№8
- 17. Алгебра 7-9 Элементы статистики и теории
- 18. Ответ: 12. А1ВСПристаньВведем обозначениямаршрутов:АА2В3В1В2С1С2Маршрут А1 В1
- 19. Слайд 19
Во взрослой жизни человеку часто приходится стоять перед выбором: куда пойти учиться, какую профессию выбрать, чтоб не оказаться в ряду безработных, какую модель поведения в себе построить, какой стиль одежды предпочесть… Другими словами, из всего
Слайд 1 «Комбинаторика – ветвь математики, изучающая комбинации и перестановки предметов, возникла в
Слайд 2Во взрослой жизни человеку часто приходится стоять перед выбором: куда пойти
учиться, какую профессию выбрать, чтоб не оказаться в ряду безработных, какую модель поведения в себе построить, какой стиль одежды предпочесть…
Другими словами, из всего возможного выбрать тот вариант, (тот путь, ту комбинацию), который приведет к положительному и лучшему исходу в сложившейся ситуации.
Во всех случаях приходится человеку прежде, чем принять решение, продумать все возможные варианты, комбинации. И при этом выбрать наилучший (говорят «оптимальный»). Вот какая связь комбинаторики с жизнью.
И, конечно, знакомство с ней начинается
с самого простого…
Слайд 3
В науке и практике часто встречаются
задачи,
решая которые
приходится составлять
различные комбинации
из конечного числа элементов
и подсчитывать количество
таких комбинаций.
Такие задачи называются комбинаторными.
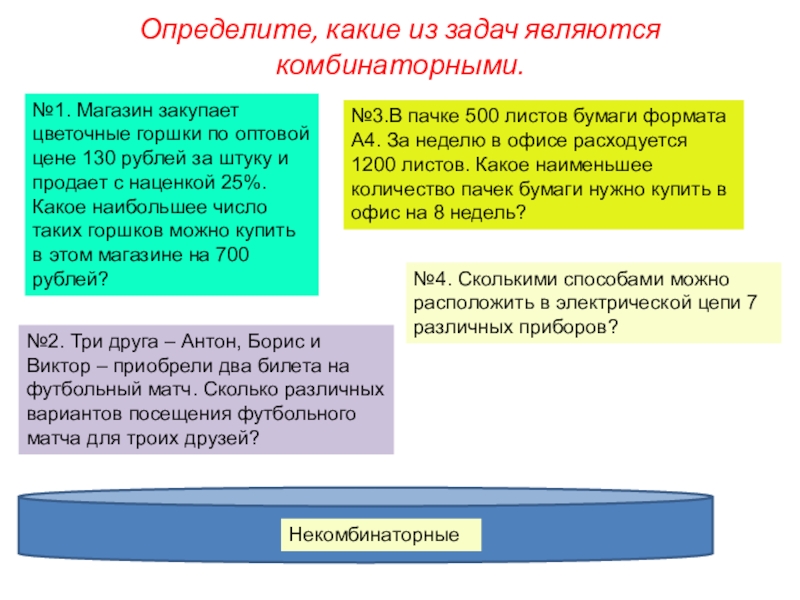
Слайд 4Определите, какие из задач являются комбинаторными.
№4. Сколькими способами можно расположить в
электрической цепи 7 различных приборов?
№2. Три друга – Антон, Борис и Виктор – приобрели два билета на футбольный матч. Сколько различных вариантов посещения футбольного матча для троих друзей?
Некомбинаторные
№1. Магазин закупает цветочные горшки по оптовой цене 130 рублей за штуку и продает с наценкой 25%. Какое наибольшее число таких горшков можно купить в этом магазине на 700 рублей?
№3.В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 1200 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 8 недель?
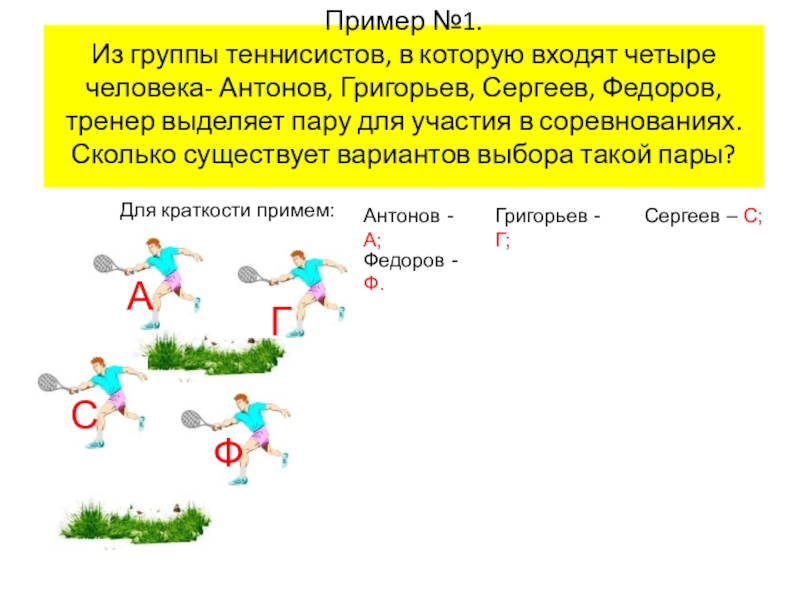
Слайд 7 Пример №1. Из группы теннисистов, в которую входят четыре человека- Антонов, Григорьев,
Сергеев, Федоров, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?
Для краткости примем:
Антонов - А;
Григорьев - Г;
Сергеев – С;
Федоров - Ф.
С
А
Г
Ф
Слайд 8
Г
С
Ф
А
Г
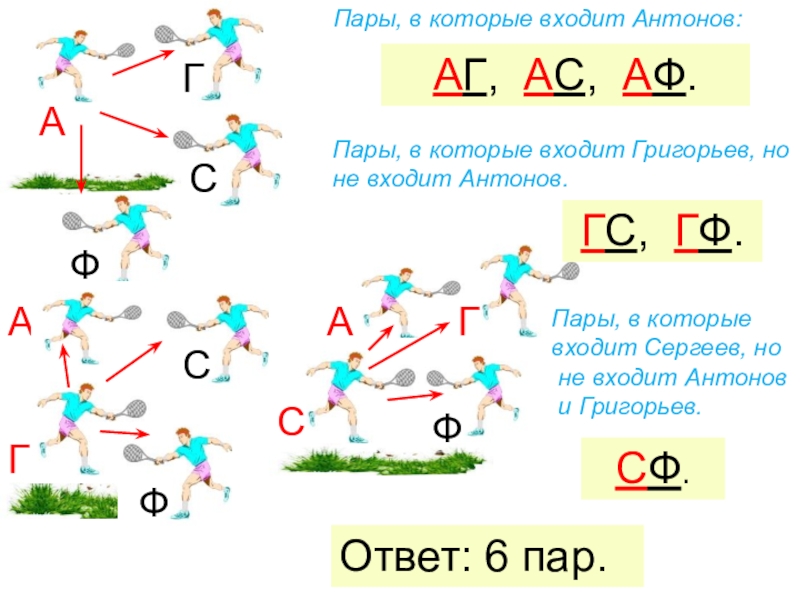
АГ, АС, АФ.
Пары, в которые входит Антонов:
С
Пары, в которые входит Григорьев,
но не входит Антонов.
ГС, ГФ.
С
Ф
Пары, в которые входит Сергеев, но
не входит Антонов
и Григорьев.
СФ.
Ответ: 6 пар.
А
Ф
А
Г
Слайд 9Пример №2. Три друга – Антон, Борис и Виктор – приобрели
два билета на футбольный матч. Сколько различных вариантов посещения футбольного матча для троих друзей?
Рассуждая по аналогии, решить задачу.
Слайд 10Решение:
Для записи трехзначного числа используем 3 цифры в классе единиц:
для разряда сотен, десятков, единиц.
Составим схему, которая называется деревом возможных вариантов.
Пример №2.
Запишите все трехзначные числа, для записи которых употребляются только цифры 0 и 7.
Найдите сумму этих чисел и разделите её на 211.
Слайд 11
7
единицы
7
0
десятки
7
0
0
7
Ответ: (777, 770, 707, 700.);
(777+770+707+700):211=14.
сотни
Для разряда сотен можно использовать только 7, иначе искомое число будет двузначным!!!
Для разряда десятков можно
использовать 0 и 7.
Для разряда единиц можно 0 и 7.
Слайд 12
Пример №3
В кафе «Минутка» предлагают
два первых блюда:
борщ, рассольник
четыре вторых блюда:
гуляш, котлеты, сосиски, пельмени.
Укажите все обеды из двух блюд, которые может заказать посетитель.
Проиллюстрируйте ответ, построив дерево возможных вариантов.
В кафе «Минутка» предлагают
два первых блюда:
борщ, рассольник
четыре вторых блюда:
гуляш, котлеты, сосиски, пельмени.
Укажите все обеды из двух блюд, которые может заказать посетитель.
Проиллюстрируйте ответ, построив дерево возможных вариантов.
Кафе «Минутка»
Слайд 13
Меню кафе «Минутка»
Первое блюдо
Борщ
Рассольник
Второе блюдо
1 Гуляш
2. Котлеты
3. Сосиски
4. Пельмени
Кафе «Минутка»
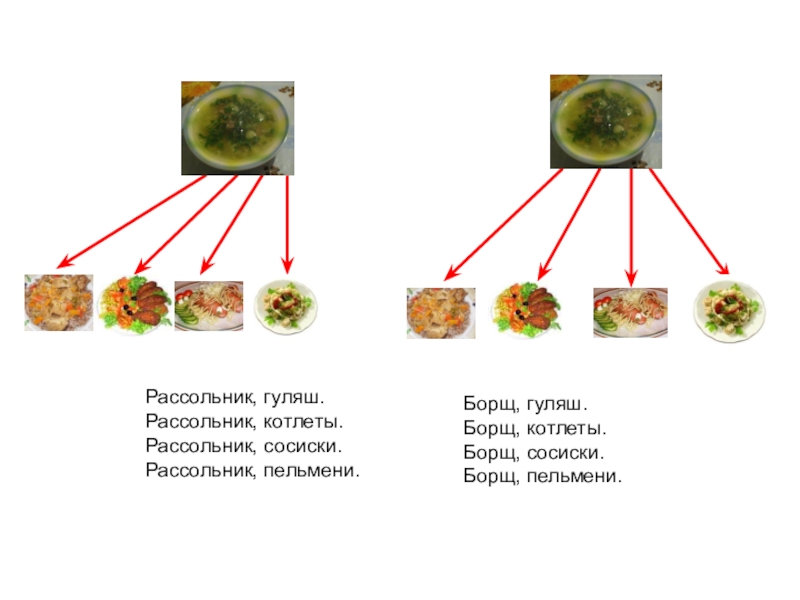
Слайд 14Рассольник, гуляш.
Рассольник, котлеты.
Рассольник, сосиски.
Рассольник, пельмени.
Борщ, гуляш.
Борщ, котлеты.
Борщ, сосиски.
Борщ, пельмени.
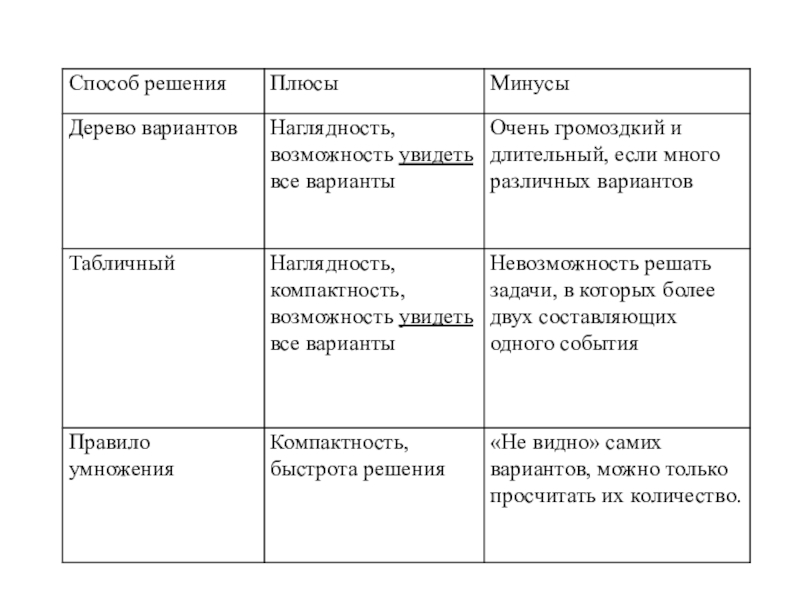
Слайд 17Алгебра 7-9 Элементы статистики
и теории вероятности (Ю.Н. Макарычев, Н.Г. Миндюк)
Пример
3(стр.39)
Правило умножения
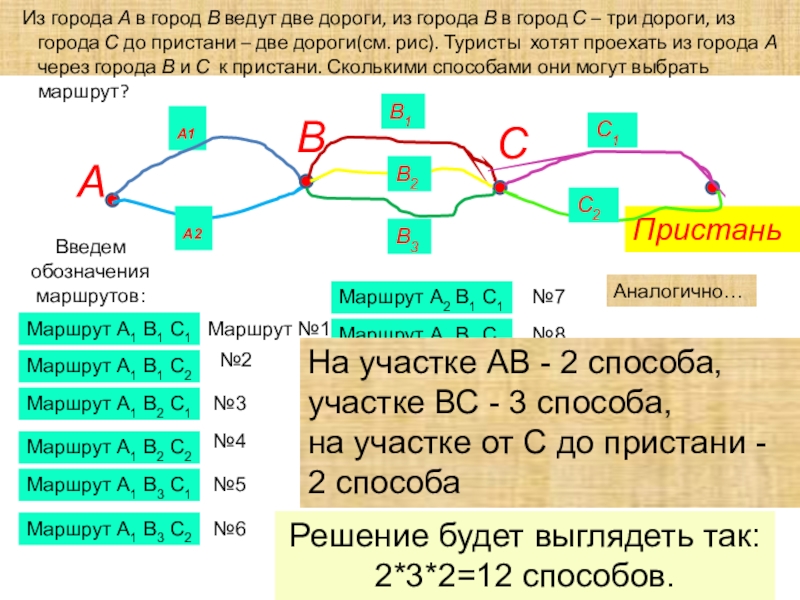
Слайд 18Ответ: 12.
А1
В
С
Пристань
Введем
обозначения
маршрутов:
А
А2
В3
В1
В2
С1
С2
Маршрут А1 В1 С1
Маршрут №1
Маршрут А1 В1
С2
№2
Маршрут А1 В2 С1
Маршрут А1 В2 С2
Маршрут А1 В3 С1
Маршрут А1 В3 С2
№4
№3
№5
№6
Маршрут А2 В1 С1
Маршрут А2 В1 С2
Маршрут А2 В2 С1
Маршрут А2 В2 С2
Маршрут А2 В3 С1
Маршрут А2 В3 С2
№8
№7
№9
№ 10
№ 11
№ 12
Решение будет выглядеть так: 2*3*2=12 способов.
Аналогично…
На участке АВ - 2 способа,
участке ВС - 3 способа,
на участке от С до пристани - 2 способа
Из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги(см. рис). Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?
