- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Пропорция
Содержание
- 1. Презентация по математике на тему Пропорция
- 2. Цель урока: изучение понятия пропорции.Задачи:1.Сформировать понятие пропорция,
- 3. План урока1.Организационный момент.2.Устные упражнения.3.Объяснение нового материала.4.Математические исследования.5.Страница истории.6.Домашнее задание.
- 4. Подумай и реши:1.Найдите отношение: а)125:5; б)3:10; в)14,4:4;
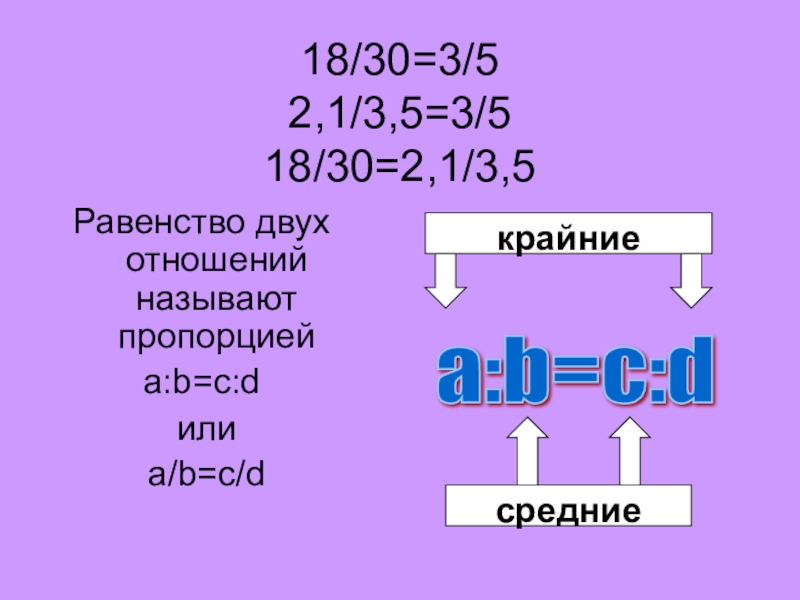
- 5. 18/30=3/5 2,1/3,5=3/5 18/30=2,1/3,5Равенство двух отношений называют пропорциейa:b=c:d или a/b=c/d
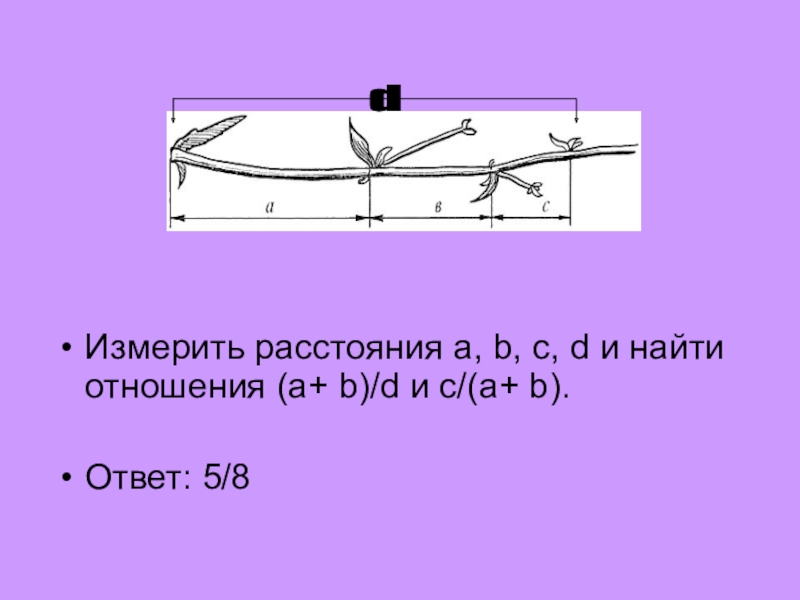
- 6. Измерить расстояния a, b, c, d и найти отношения (a+ b)/d и c/(a+ b).Ответ: 5/8d
- 7. Одним из красивейших произведений древнегреческой архитектуры является
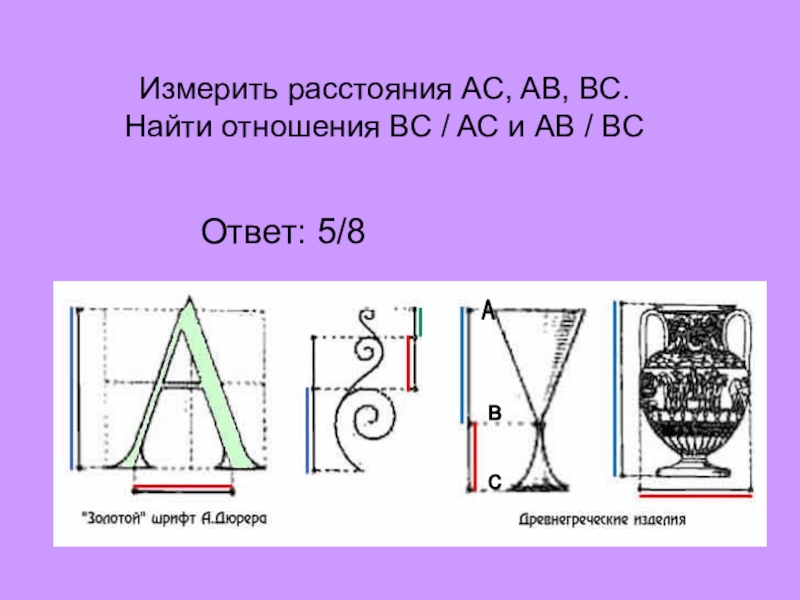
- 8. Измерить расстояния AC, AB, BC. Найти отношения
- 9. Слово пропорция означает «соразмерность», «определенное соотношение частей
- 10. Принято считать, что понятие о золотом делении
- 11. Золотое сечение в картине И. И. Шишкина"Сосновая
- 12. Скульпторы утверждают, что талия делит совершенное человеческое
- 13. Природа распорядилась в строении человеческого тела следующими
- 14. Длина четырёх пальцев равна длине ладони.Расстояние от
- 15. Домашнее заданиеНайдите предметы, окружающие вас, которые дают
Цель урока: изучение понятия пропорции.Задачи:1.Сформировать понятие пропорция, умение составлять и читать пропорции..2.Развивать чувство гармонии, прекрасного.3.Показать практическое применение этого понятия.4.Учить анализировать и делать выводы.
Слайд 2Цель урока: изучение понятия пропорции.
Задачи:
1.Сформировать понятие пропорция, умение составлять и читать
пропорции..
2.Развивать чувство гармонии, прекрасного.
3.Показать практическое применение этого понятия.
4.Учить анализировать и делать выводы.
2.Развивать чувство гармонии, прекрасного.
3.Показать практическое применение этого понятия.
4.Учить анализировать и делать выводы.
Слайд 3План урока
1.Организационный момент.
2.Устные упражнения.
3.Объяснение нового материала.
4.Математические исследования.
5.Страница истории.
6.Домашнее задание.
Слайд 4Подумай и реши:
1.Найдите отношение: а)125:5; б)3:10; в)14,4:4; г)45:20; д)0,1:0,6.
Ответ: а)25; б)0,3;
в)3,6; г)9/4; д)1/6
2.Крутизной лестницы называют отношение высоты ступеньки к её глубине. Чему равна крутизна лестницы, если высота ступеньки 18см, а глубина 30см?
Ответ: 18/30=3/5
3.Для варенья на 2,1 кг ягод было взято 3,5 кг сахарного песка. В каком отношении по массе были взяты ягоды и сахарный песок?
Ответ: 2,1/3,5=3/5
2.Крутизной лестницы называют отношение высоты ступеньки к её глубине. Чему равна крутизна лестницы, если высота ступеньки 18см, а глубина 30см?
Ответ: 18/30=3/5
3.Для варенья на 2,1 кг ягод было взято 3,5 кг сахарного песка. В каком отношении по массе были взяты ягоды и сахарный песок?
Ответ: 2,1/3,5=3/5
Слайд 518/30=3/5
2,1/3,5=3/5
18/30=2,1/3,5
Равенство двух отношений называют пропорцией
a:b=c:d
или
a/b=c/d
Слайд 7Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до
н. э.).
Измерить расстояния AC, AB, BC.
Найти отношения BC / AC и AB / BC
Ответ: 5/8
A
B
C
Слайд 9Слово пропорция означает «соразмерность», «определенное соотношение частей между собой».
Деление целого
на две неравные части, при котором большая часть так относится к целому, как меньшая к большей называют«золотым сечением» и даже «божественной пропорцией». Это отношение приближенно равно 0,618 ≈ 5/8.
В геометрии «золотым сечением» называется также деление отрезка в среднем и крайнем отношении.
Пропорции «золотого сечения» создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях.
Золотое сечение применяется в произведениях искусства, архитектуре, развитии ремесел, встречается в природе.
В геометрии «золотым сечением» называется также деление отрезка в среднем и крайнем отношении.
Пропорции «золотого сечения» создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях.
Золотое сечение применяется в произведениях искусства, архитектуре, развитии ремесел, встречается в природе.
Слайд 10Принято считать, что понятие о золотом делении ввел в научный обиход
Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре.
В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре.
В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели.
Слайд 11
Золотое сечение в картине И. И. Шишкина"Сосновая роща"
На этой знаменитой картине
И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен - при желании можно с успехом продолжить деление картины по золотому сечению и дальше.
Слайд 12Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении «золотого
сечения».
Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям.
Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям.
Слайд 13Природа распорядилась в строении человеческого тела следующими пропорциями:
четыре ладони равны стопе,
шесть
ладоней составляют один локоть,
четыре локтя - рост человека,
четыре локтя равны шагу, а двадцать четыре ладони равны росту человека,
наибольшая ширина плеч - восьмая часть роста,
расстояние от локтя до кончиков пальцев - 1/5 роста, от локтя до подмышечной ямки - 1/8,
длина всей руки - это 1/10 роста,
стопа - 1/7 часть роста.
четыре локтя - рост человека,
четыре локтя равны шагу, а двадцать четыре ладони равны росту человека,
наибольшая ширина плеч - восьмая часть роста,
расстояние от локтя до кончиков пальцев - 1/5 роста, от локтя до подмышечной ямки - 1/8,
длина всей руки - это 1/10 роста,
стопа - 1/7 часть роста.
Слайд 14Длина четырёх пальцев равна длине ладони.
Расстояние от кончика подбородка до носа
и от корней волос до бровей будет одинаково и, подобно длине уха, равно 1/3 лица.
Слайд 15Домашнее задание
Найдите предметы, окружающие вас, которые дают примеры золотого сечения
Проверьте, в
каком отношении находятся части вашего тела.