- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Применение производной к исследованию функций. Построение графика функции.
Содержание
- 1. Презентация по математике на тему Применение производной к исследованию функций. Построение графика функции.
- 2. 1. Вопросы по теории:1) Какая функция называется
- 3. Дана функция y=f(x), убывающая на
- 4. Доказательство этих признаков проводится на основании формулы
- 5. 3. Внутренние точки области определения функции, в
- 6. Определение. - точка минимума для функции f,
- 7. Дана функция y=f(x). Найдите1) область определения функции;2)
- 8. xy-66Y=f '(x)На рисунке изображён график производной функции
- 9. xyY=f '(x)К графику функции y = f(x)
- 10. На рисунке изображен график функции f(x) =
- 11. Стих о производнойВ данной функции от икс,
Слайд 1Применение производной к исследованию функций. Построение графика функции.
Презентацию подготовила: Седых
учитель математики
МБОУ Бобровская СОШ № 1
Слайд 2
1.
Вопросы по теории:
1) Какая функция называется возрастающей?
2) Какая функция называется
3) Какие точки функции называются точками экстремума?
tg α > 0, f’(x) > 0
0 a b X
2.Дана функция y=f’(x), возрастающая на (a;b).
α
Теорема. Если f’(x)>0 в каждой точке интервала (a;b), то функция возрастает на (a;b).
y
Слайд 3
Дана функция y=f(x), убывающая на (a;b)
tg α < 0,
a b x
Теорема. Если f’(x)<0 в каждой точке интервала (a;b), то функция f(x) убывает на (a;b).
y
α
Слайд 4Доказательство этих признаков проводится на основании формулы Лагранжа:
Пусть x1 € (a;
По формуле Лагранжа Ә c € (x1; x2), такое что
1) Если f’(x) > 0, то f(x2) - f(x1);
2) Если f’(x) < 0, то f(x2) - f(x1);
Вывод
1) Достаточный признак возрастания функции на интервале: f’(x) > 0.
2) Достаточный признак убывания функции на интервале: f’(x) < 0.
Слайд 5
3. Внутренние точки области определения функции, в которых её производная равна
Теорема Ферма (необходимое условие экстремума). Если функция f(x) определена в окрестности точки x0, точка x0 является точкой экстремума и в этой точке существует производная f’(x0)=0.
y
+ -
0 a x0 b x
4. Определение. x0 – точка максимума функции f, если для V x из некоторой окрестности x0 f(x) ≤ f(x0).
y=f(x)
Признак максимума функции.
Если в точке производная меняет знак с «плюса» на «минус», то есть точка максимума.
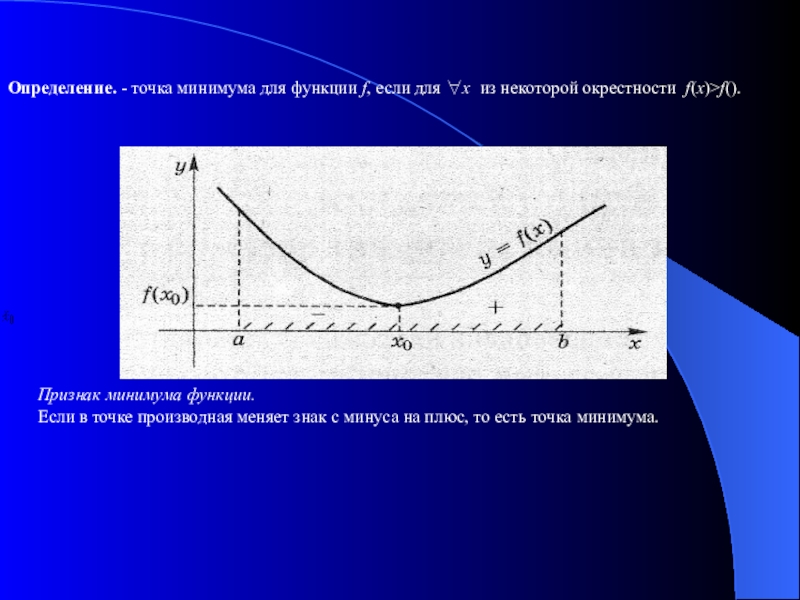
Слайд 6Определение. - точка минимума для функции f, если для ∀x из
Признак минимума функции.
Если в точке производная меняет знак с минуса на плюс, то есть точка минимума.
Слайд 7
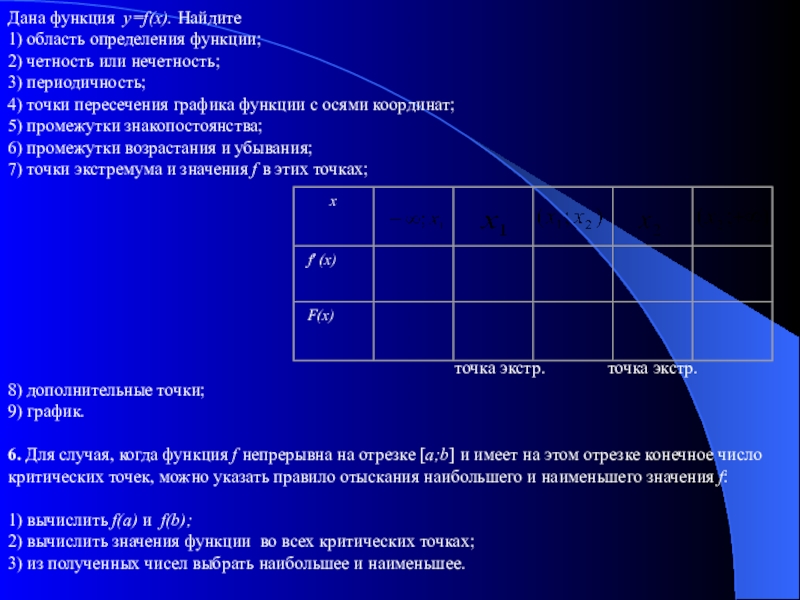
Дана функция y=f(x). Найдите
1) область определения функции;
2) четность или нечетность;
3) периодичность;
4)
5) промежутки знакопостоянства;
6) промежутки возрастания и убывания;
7) точки экстремума и значения f в этих точках;
точка экстр. точка экстр.
8) дополнительные точки;
9) график.
6. Для случая, когда функция f непрерывна на отрезке [a;b] и имеет на этом отрезке конечное число критических точек, можно указать правило отыскания наибольшего и наименьшего значения f:
1) вычислить f(a) и f(b);
2) вычислить значения функции во всех критических точках;
3) из полученных чисел выбрать наибольшее и наименьшее.
Слайд 8
x
y
-6
6
Y=f '(x)
На рисунке изображён график производной функции y= f/ (x), заданной
[-6; 6].Исследуйте функцию y=f(x) на монотонность и укажите в ответе число
промежутков убывания.
Слайд 9
x
y
Y=f '(x)
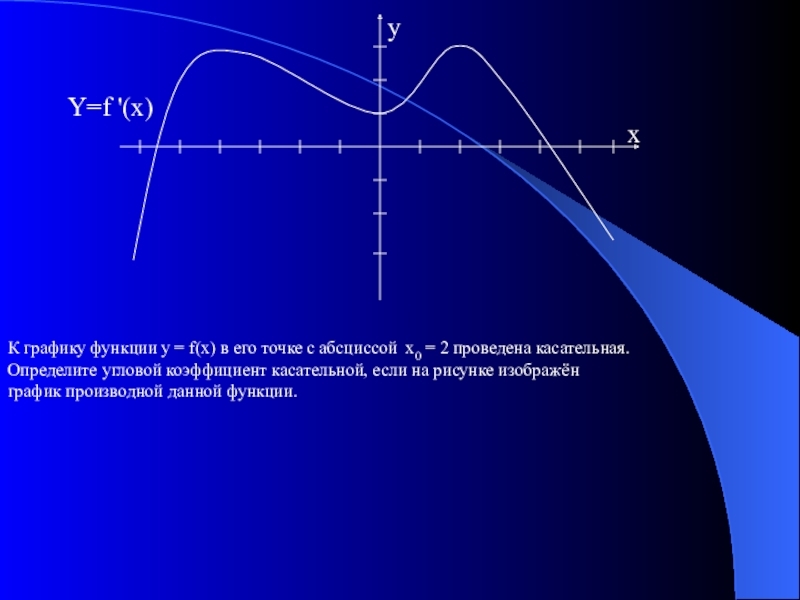
К графику функции y = f(x) в его точке с
Определите угловой коэффициент касательной, если на рисунке изображён
график производной данной функции.
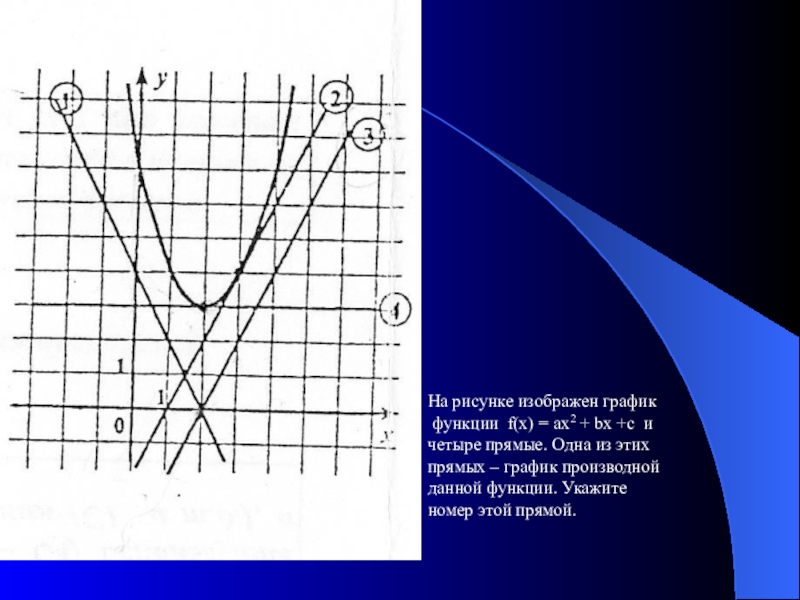
Слайд 10На рисунке изображен график
функции f(x) = ax2 + bx +c
четыре прямые. Одна из этих
прямых – график производной
данной функции. Укажите
номер этой прямой.
Слайд 11Стих о производной
В данной функции от икс, наречённой игреком,
Вы фиксируете икс,
Придаёте вы ему тотчас приращение,
Тем у функции самой вызвав изменение.
Приращений тех теперь, взявши отношение,
Пробуждаете к нулю дельта икс стремление.
Предел такого отношенья вычисляется,
Он производною в науке называется.





![Презентация по математике на тему Применение производной к исследованию функций. Построение графика функции. xy-66Y=f '(x)На рисунке изображён график производной функции y= f/ (x), заданной xy-66Y=f '(x)На рисунке изображён график производной функции y= f/ (x), заданной на отрезке [-6; 6].Исследуйте функцию y=f(x)](/img/thumbs/cb086a94d410473a28d55d9fcebb5c24-800x.jpg)