- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Приближенные вычисления
Содержание
- 1. Презентация по математике на тему Приближенные вычисления
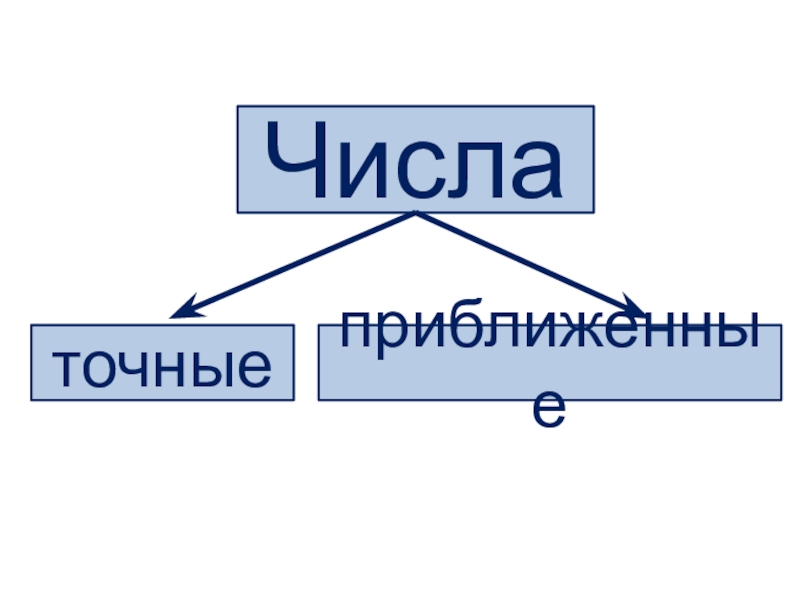
- 2. Числаточныеприближенные
- 3. Теория приближенных вычислений позволяет:зная степень точности
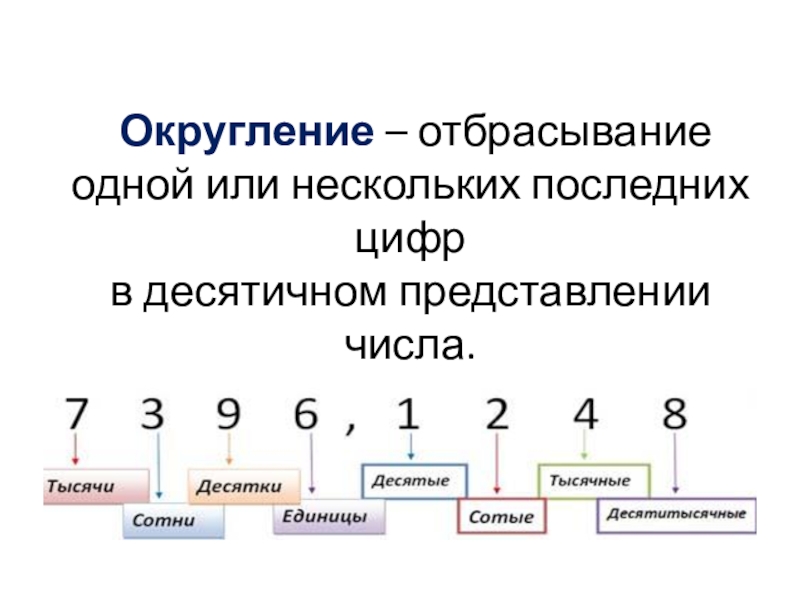
- 4. Округление – отбрасывание одной или нескольких последних цифр в десятичном представлении числа.
- 5. Правила округления чиселЕсли первая из отбрасываемых цифр
- 6. Если первая из отбрасываемых цифр меньше 5,
- 7. Абсолютная и относительная погрешности Разность между точным числом
- 8. Приближенные вычисления с помощью правил подсчета цифр
- 9. Приближенные вычисления по способу границ НГ
Числаточныеприближенные
Слайд 3Теория приближенных
вычислений позволяет:
зная степень точности данных, оценить степень точности результатов;
брать
данные с надлежащей степенью точности, достаточной для обеспечения требуемой точности результата;
рационализировать процесс вычисления.
рационализировать процесс вычисления.
Слайд 4 Округление – отбрасывание одной или нескольких последних цифр в десятичном представлении
числа.
Слайд 5Правила округления чисел
Если первая из отбрасываемых цифр
больше 5, то последняя
из сохраняющихся цифр увеличивается на 1.
Если первая из отбрасываемых цифр равна 5,
а за ней следуют одна или несколько значащих цифр, то последняя из сохраняющихся цифр
также увеличивается на 1.
Слайд 6Если первая из отбрасываемых цифр меньше 5, то последняя из сохраняемых
цифр остаётся неизменной.
Если отбрасывается цифра 5, а за ней нет и никогда не было значащих цифр, то последняя из сохраняемых цифр остаётся неизменной, если она чётная, и увеличивается на 1, если она нечётная.
Если отбрасывается цифра 5, а за ней нет и никогда не было значащих цифр, то последняя из сохраняемых цифр остаётся неизменной, если она чётная, и увеличивается на 1, если она нечётная.
Слайд 7Абсолютная и относительная погрешности
Разность между точным числом
и его приближенным значением
называется абсолютной погрешностью приближенного числа.
Относительной погрешностью называется отношение абсолютной погрешности к величине приближенного числа.
Относительной погрешностью называется отношение абсолютной погрешности к величине приближенного числа.
Слайд 8Приближенные вычисления с помощью правил подсчета цифр
При сложении и вычитании приближенных
чисел
в результате следует сохранять столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков.
При умножении и делении приближенных чисел в произведении надо сохранить столько значащих цифр, сколько их есть в данном числе с наименьшим количеством значащих цифр.
При возведении приближенных чисел в квадрат, и куб в результате сохраняется столько значащих цифр, сколько их в основании.
При умножении и делении приближенных чисел в произведении надо сохранить столько значащих цифр, сколько их есть в данном числе с наименьшим количеством значащих цифр.
При возведении приближенных чисел в квадрат, и куб в результате сохраняется столько значащих цифр, сколько их в основании.
Слайд 9Приближенные вычисления
по способу границ
НГ ( x + у ) =
НГ х + HГ y ; ВГ ( х + у ) = ВГ х + ВГ y
НГ ( ху ) = НГ х · НГ у ; ВГ ( х у) = ВГ х · ВГ y
НГ ( х - у ) = НГ х - ВГ у ; ВГ ( х - у ) = ВГ х - НГ у
НГ ( ху ) = НГ х · НГ у ; ВГ ( х у) = ВГ х · ВГ y
НГ ( х - у ) = НГ х - ВГ у ; ВГ ( х - у ) = ВГ х - НГ у