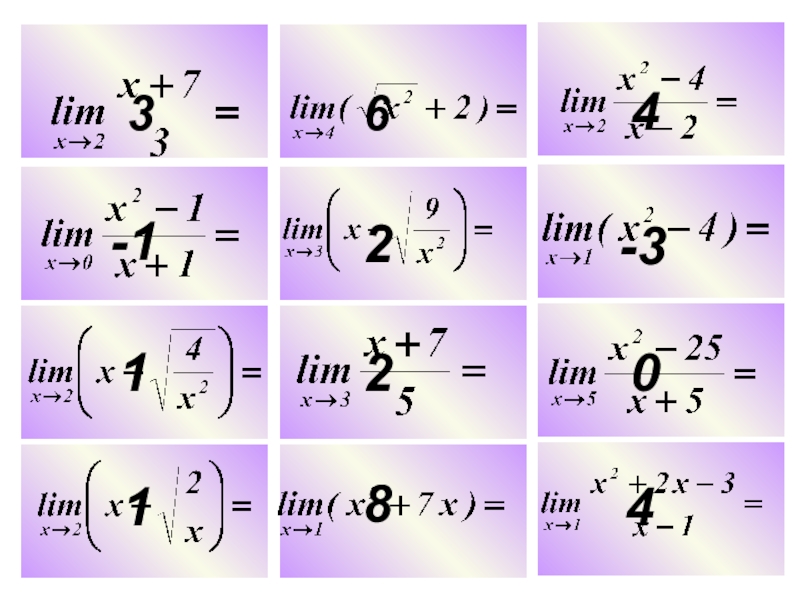Задачи: 1. Научиться вычислять предел функции на бесконечности.
2. Познакомиться с геометрической интерпретацией предела функции на бесконечности.
3. Рассмотреть случаи применения предела функции в экономике.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Предел функции на бесконечности
Содержание
- 1. Презентация по математике на тему Предел функции на бесконечности
- 2. Проверка домашнего заданияСформулировать определение предела функции в
- 3. Слайд 3
- 4. Какие методы и приемы мы используем, когда
- 5. Математическоелото
- 6. 36 4 -1 2 -3 1 2 0 1 8 4
- 7. Вопрос 5Дана дробь. Что происходит с ее
- 8. Дана дробь. Что происходит с ее значением, если постепенно уменьшать ее знаменатель?2=21,510,90,80,70,60,51,051,332,002,222,504,002,853,335,0011,90,4Вопрос 6Актуализация знаний
- 9. Изучение нового материала
- 10. Определение предела функции на бесконечностиКроме предела
- 11. y 1Геометрическая
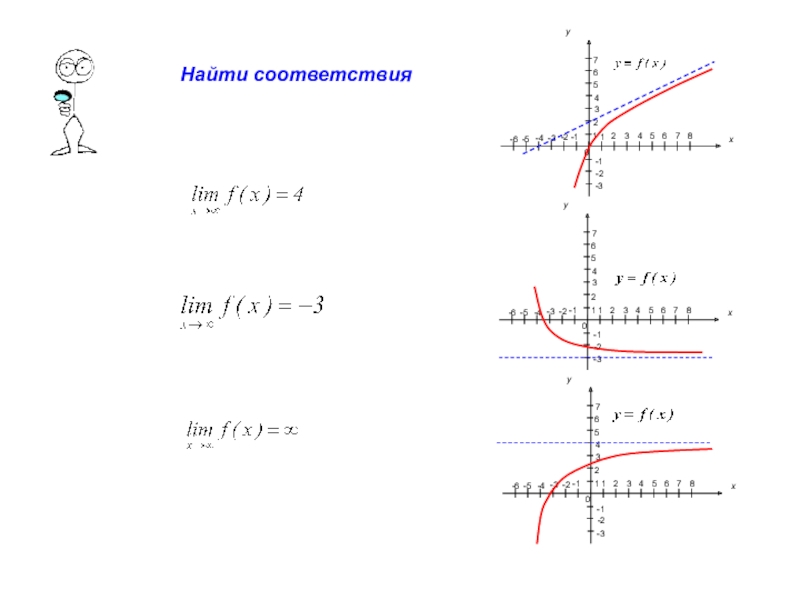
- 12. Найти соответствия
- 13. Вычисление пределов функцийна бесконечности
- 14. Пример. Вычислите предел функцииРешение.Ответ:Правило 1. Если старшая
- 15. Пример. Вычислите предел функцииРешение.Ответ:Правило 2. Если старшая
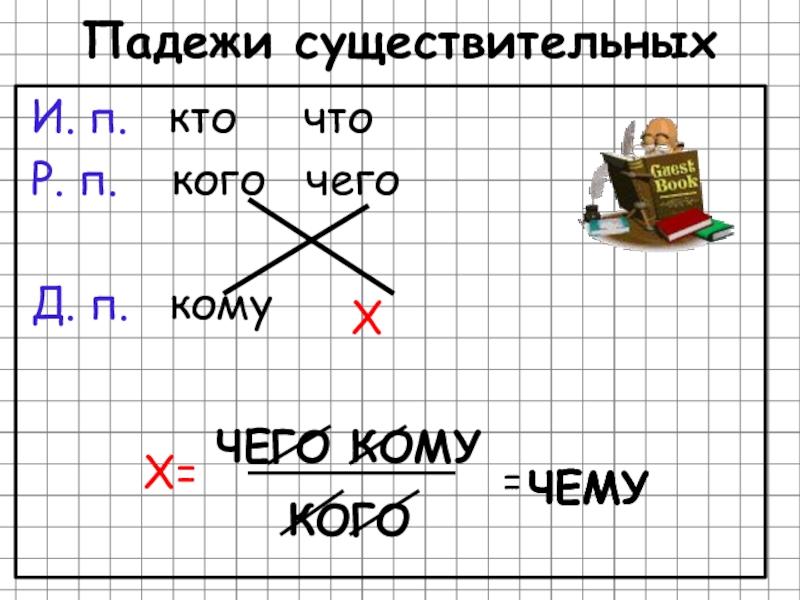
- 16. Падежи существительныхКОГОЧЕГО КОМУ=ЧЕМУХ=И. п. кто
- 17. Пример. Вычислите предел функцииРешение.Ответ:Правило 3. Если старшая
- 18. Вывод:
- 19. отдохнем !
- 20. ПРЕДЕЛЫ В ЭКОНОМИКЕ
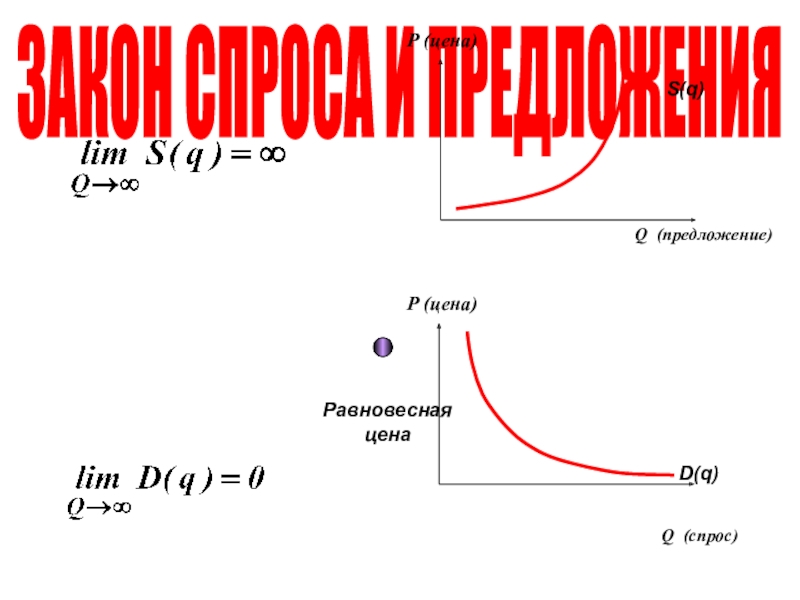
- 21. ЗАКОН СПРОСА И ПРЕДЛОЖЕНИЯРавновесная цена
- 22. Слайд 22
- 23. Спасибо за вниманиедо встречи!
Слайд 1Тема: Предел функции на бесконечности
Цель урока: Изучить понятие
Слайд 2Проверка домашнего задания
Сформулировать определение предела функции в точке.
Вопрос 1
Вопрос 2
Сформулировать свойства
Слайд 4Какие методы и приемы мы используем, когда избавляемся от неопределенности вида
Вопрос 3
Вопрос 4
Что происходит при делении степени на степень?
Проверка домашнего задания
Слайд 7Вопрос 5
Дана дробь. Что происходит с ее значением, если постепенно увеличивать
3
=
3
5
6
7
8
9
10
11
0,75
0,6
0,5
0,42
0,38
0,27
0,33
0,30
0,25
1
4
12
Актуализация знаний
“Человек есть дробь. Числитель это – сравнительно с другими – достоинства человека; знаменатель – это оценка человеком самого себя. Увеличить своего числителя – свои достоинства – не во власти человека, но всякий может уменьшить своего знаменателя – свое мнение о самом себе, и этим уменьшением приблизиться к совершенству.”
(Л. Н. Толстой)
Слайд 8
Дана дробь. Что происходит с ее значением, если постепенно уменьшать
2
=
2
1,5
1
0,9
0,8
0,7
0,6
0,5
1,05
1,33
2,00
2,22
2,50
4,00
2,85
3,33
5,00
1
1,9
0,4
Вопрос 6
Актуализация знаний
Слайд 10Определение
предела функции на бесконечности
Кроме предела функции в точке существует понятие
Определение. Число А называется пределом функции f(x) при если при достаточно больших значениях аргумента, соответствующая последовательность значений функции стремится к числу А.
Обозначение
Слайд 11y 1
Геометрическая интерпретация предела функции на
Если 111.111.111 умножить на
111.111.111, то получится
12345678987654321
Слайд 14Пример. Вычислите предел функции
Решение.
Ответ:
Правило 1.
Если старшая степень переменной числителя равна
Во всем просвещенном мире вызвало сенсацию заявление о том, что одна из «семи математических задач тысячелетия» — гипотеза Пуанкаре — доказана. Доказал ее российский математик-гений Григорий Перельман.
Все удивляются, что отказался - китайцы, американцы, русские. Ведь 1000000 $ , и не взял. И за наградой не поехал. Учредители предлагали ему варианты:
а) примите награду, приезжайте за медалью и деньгами;
б) примите награду, не приезжайте, а медаль и чек мы вам пришлем;
в) не принимайте.
Перельман выбрал вариант «в».
Слайд 15Пример. Вычислите предел функции
Решение.
Ответ:
Правило 2.
Если старшая степень переменной числителя больше
Слайд 17Пример. Вычислите предел функции
Решение.
Ответ:
Правило 3.
Если старшая степень переменной числителя меньше
Слайд 22
Знать теоретический материал.
Вычислить пределы функций
3. Придумать пример на вычисление предела функции на бесконечности, сдать задание на следующем занятии, фамилию на листе не подписывать.