- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Построение графиков функций, содержащих знак целой и дробной части
Содержание
- 1. Презентация по математике на тему Построение графиков функций, содержащих знак целой и дробной части
- 2. Вспомним!Целой частью числа x называется наибольшее целое
- 3. Вычислите:[1,5] = [ 3] = [-1,3] =
- 4. Функция y=[x]
- 5. D([x]) = RНи четная, ни нечетная Не
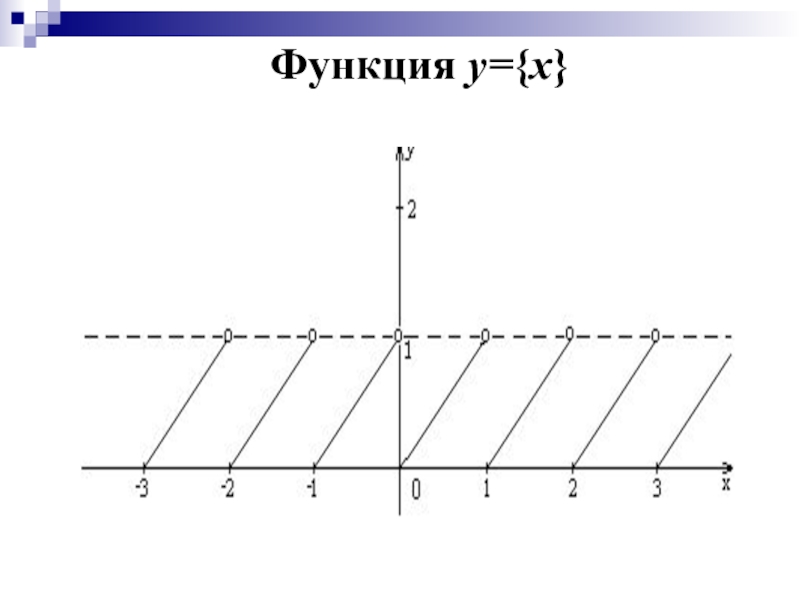
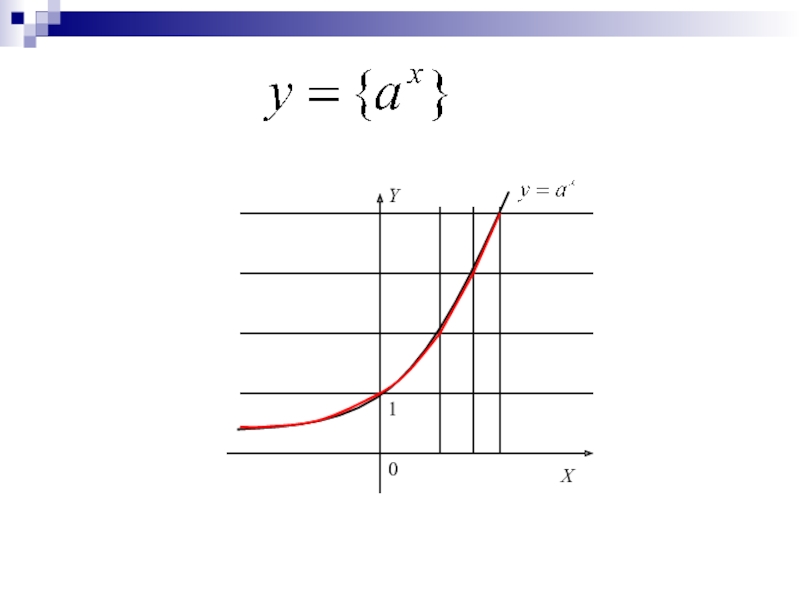
- 6. Функция y={x}
- 7. Свойства функции y={x}D({x}) = RНи четная, ни
- 8. Построение графика функции y=[f(x)]Строим прямые y=n, рассматриваем
- 9. y=[arcsinx]XY01y=arcsinx
- 10. Построение графика функции y=f([x]) Строим прямые x=n
- 11. XY10
- 12. Построение графика функции y={f(x)}Cтроим прямые y=n В
- 13. XY01
- 14. Построение графика функции y=f({x})Легко заметить, что такие
- 15. XY01
- 16. Самостоятельно! Построить графики вида y=f([x]), y=[f(x)], y=f({x}), y={f(x)}, гдеf(x)=cosxf(x)=sinx
Вспомним!Целой частью числа x называется наибольшее целое число n, не превышающее x Дробной частью числа называют разность между самим числом x и его целой частью:
Слайд 2Вспомним!
Целой частью числа x называется наибольшее целое число n, не превышающее
x
Дробной частью числа называют разность между самим числом x и его целой частью:
Дробной частью числа называют разность между самим числом x и его целой частью:
Слайд 5
D([x]) = R
Ни четная, ни нечетная
Не периодическая
E ([x]) = Z
Неограниченна
Разрывная
Нулями функции будут все значения [0;1)
Принимает отрицательные значения при x<0, и положительные значения при x>1
Неубывающая
Точек экстремума нет, так как не меняет характер монотонности
Не принимает наибольшего и наименьшего значений на области определения, т.к. постоянна на каждом интервале [n ; n+1)
Свойства функции y=[x]
Слайд 7Свойства функции y={x}
D({x}) = R
Ни четная, ни нечетная
Периодическая с наименьшим положительным
периодом T = 1;
E({x}) = [0,1)
Ограничена
Непрерывна на каждом интервале [n ; n+1), где n – целое, в каждой точке n функция терпит разрыв
Нулями функции являются все целочисленные значения аргумента
На всей области определения принимает только положительные значения
Строго монотонно возрастающая на каждом интервале [n, n+1)
Точек экстремума нет, так как не меняет характер монотонности
На каждом интервале [n; n+1) функция y = {x} принимает минимальное значение в точке n
E({x}) = [0,1)
Ограничена
Непрерывна на каждом интервале [n ; n+1), где n – целое, в каждой точке n функция терпит разрыв
Нулями функции являются все целочисленные значения аргумента
На всей области определения принимает только положительные значения
Строго монотонно возрастающая на каждом интервале [n, n+1)
Точек экстремума нет, так как не меняет характер монотонности
На каждом интервале [n; n+1) функция y = {x} принимает минимальное значение в точке n
Слайд 8Построение графика функции y=[f(x)]
Строим прямые y=n, рассматриваем полосу y=n и y=n+1
Точки
пересечения прямых y=n, y=n+1 с графиком функции y=f(x) будут принадлежать графику функции y=[f(x)], остальные точки графика y=[f(x)] в рассматриваемой полосе получим как проекцию части графика y=f(x) на прямую y=n
В каждой другой полосе, где есть точки графика функции y=f(x), построение проводится аналогично
В каждой другой полосе, где есть точки графика функции y=f(x), построение проводится аналогично
y=f(x)
0
X
Y
1
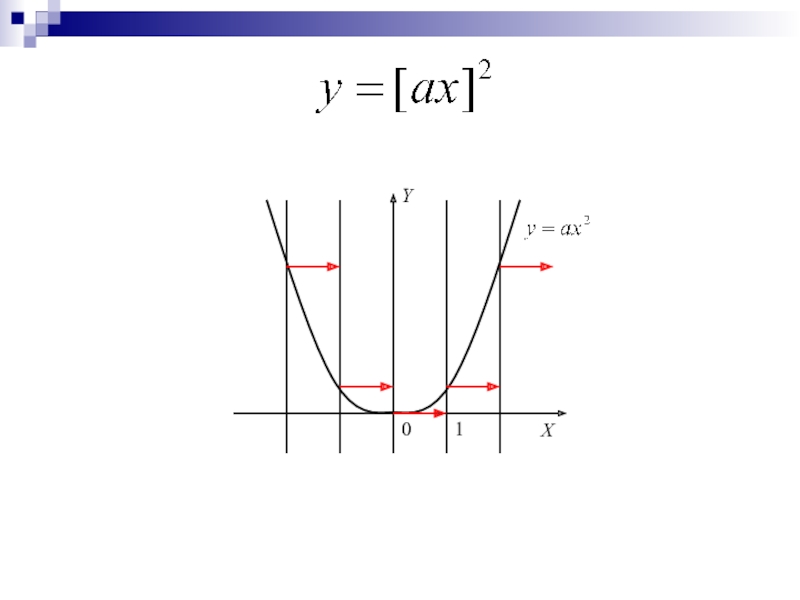
Слайд 10Построение графика функции y=f([x])
Строим прямые x=n и рассматриваем одну из
полос, образованную линиями x=n, x=n+1
Точки пересечения графика функции y=f(x) с прямыми y=n принадлежат графику функции y=f([x]), поскольку их абсциссы - целые числа; другие точки графика функции y=f([x]) в рассматриваемой полосе получим как проекцию части графика функции y=f(x), которая находится в этой полосе, на прямую y=f(n)
В каждой другой полосе, где есть точки графика функции y=f(x), построение производится аналогично
Точки пересечения графика функции y=f(x) с прямыми y=n принадлежат графику функции y=f([x]), поскольку их абсциссы - целые числа; другие точки графика функции y=f([x]) в рассматриваемой полосе получим как проекцию части графика функции y=f(x), которая находится в этой полосе, на прямую y=f(n)
В каждой другой полосе, где есть точки графика функции y=f(x), построение производится аналогично
0
1
y=f(x)
Y
X
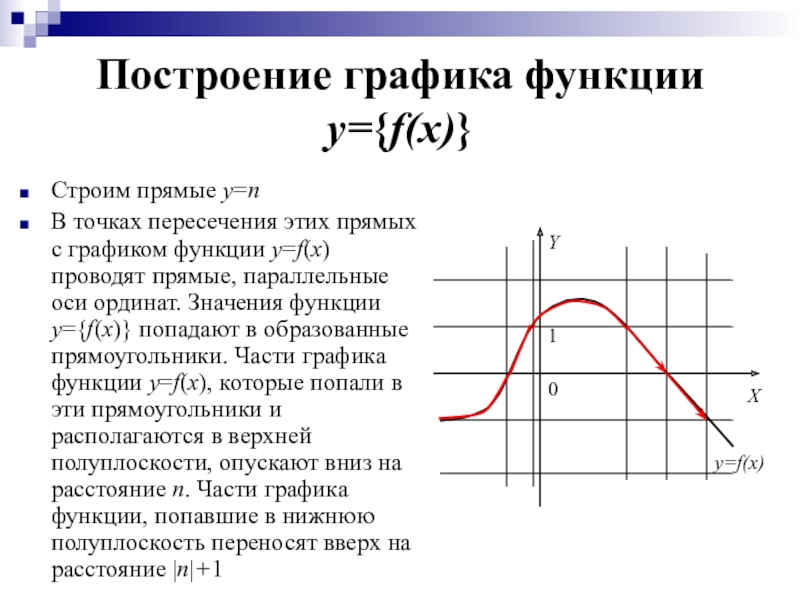
Слайд 12Построение графика функции y={f(x)}
Cтроим прямые y=n
В точках пересечения этих прямых
с графиком функции y=f(x) проводят прямые, параллельные оси ординат. Значения функции y={f(x)} попадают в образованные прямоугольники. Части графика функции y=f(x), которые попали в эти прямоугольники и располагаются в верхней полуплоскости, опускают вниз на расстояние n. Части графика функции, попавшие в нижнюю полуплоскость переносят вверх на расстояние |n|+1
y=f(x)
X
Y
1
0
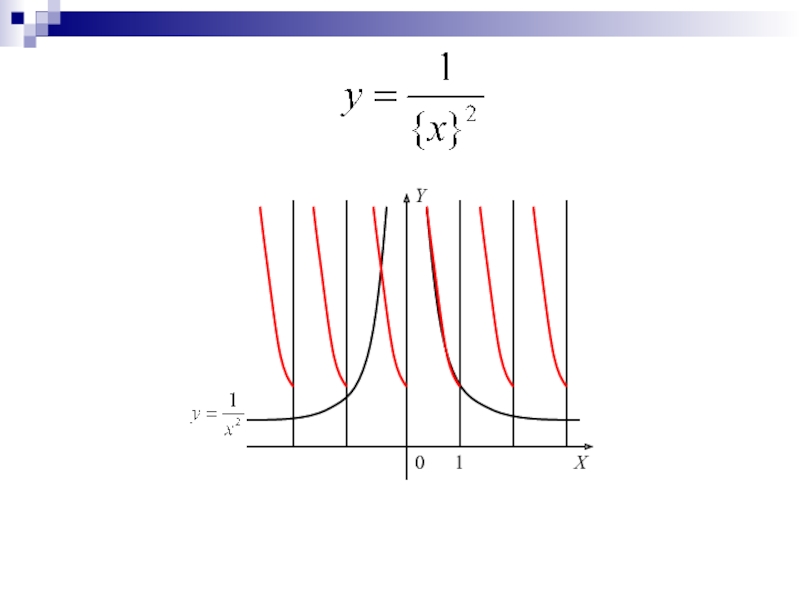
Слайд 14Построение графика функции y=f({x})
Легко заметить, что такие функции периодичны с периодом
T=1, и на отрезке [0; 1] f({x})=f(x). Отсюда следует способ построения графика функции y=f({x}):
строят график функции y=f(x) на [0; 1)
продолжают этот график, учитывая свойство периодичности функции y=f({x})
строят график функции y=f(x) на [0; 1)
продолжают этот график, учитывая свойство периодичности функции y=f({x})
X
0
1
Y
y=f(x)


![Презентация по математике на тему Построение графиков функций, содержащих знак целой и дробной части Вычислите:[1,5] = [ 3] = [-1,3] = [-4] = { 2,37} Вычислите:[1,5] = [ 3] = [-1,3] = [-4] = { 2,37} = { 3,14} = {5} ={-2,5}](/img/thumbs/a146fa956772ada97af57e3dd0f5e9fa-800x.jpg)
![Презентация по математике на тему Построение графиков функций, содержащих знак целой и дробной части Функция y=[x] Функция y=[x]](/img/thumbs/88044cd32ca648d4bf740894434f9b4f-800x.jpg)
![Презентация по математике на тему Построение графиков функций, содержащих знак целой и дробной части D([x]) = RНи четная, ни нечетная Не периодическаяE ([x]) = ZНеограниченнаРазрывная D([x]) = RНи четная, ни нечетная Не периодическаяE ([x]) = ZНеограниченнаРазрывная Нулями функции будут все значения [0;1)Принимает](/img/thumbs/12f0870891ed83bd29fe2c0a831e4bd2-800x.jpg)

![Презентация по математике на тему Построение графиков функций, содержащих знак целой и дробной части Построение графика функции y=[f(x)]Строим прямые y=n, рассматриваем полосу y=n и y=n+1Точки Построение графика функции y=[f(x)]Строим прямые y=n, рассматриваем полосу y=n и y=n+1Точки пересечения прямых y=n, y=n+1 с графиком](/img/thumbs/ca5b9aa488a32d146eded046ae65c20e-800x.jpg)
![Презентация по математике на тему Построение графиков функций, содержащих знак целой и дробной части y=[arcsinx]XY01y=arcsinx y=[arcsinx]XY01y=arcsinx](/img/thumbs/d2789554af8fd6b32005d9729c83f7da-800x.jpg)
![Презентация по математике на тему Построение графиков функций, содержащих знак целой и дробной части Построение графика функции y=f([x]) Строим прямые x=n и рассматриваем одну из Построение графика функции y=f([x]) Строим прямые x=n и рассматриваем одну из полос, образованную линиями x=n, x=n+1Точки пересечения](/img/thumbs/73a3bb8b5e034ba77ab8d3a4e63d3197-800x.jpg)
![Презентация по математике на тему Построение графиков функций, содержащих знак целой и дробной части Построение графика функции y=f({x})Легко заметить, что такие функции периодичны с периодом Построение графика функции y=f({x})Легко заметить, что такие функции периодичны с периодом T=1, и на отрезке [0; 1] f({x})=f(x).](/img/thumbs/d269bf17c62a257d3f357538ab12e5d3-800x.jpg)
![Презентация по математике на тему Построение графиков функций, содержащих знак целой и дробной части Самостоятельно! Построить графики вида y=f([x]), y=[f(x)], y=f({x}), y={f(x)}, гдеf(x)=cosxf(x)=sinx Самостоятельно! Построить графики вида y=f([x]), y=[f(x)], y=f({x}), y={f(x)}, гдеf(x)=cosxf(x)=sinx](/img/thumbs/ce24b6fd543c2938ab9418e41d999152-800x.jpg)





