- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Понятие о непрерывности функции для студентов 1 курса
Содержание
- 1. Презентация по математике на тему Понятие о непрерывности функции для студентов 1 курса
- 2. Понятие непрерывностифункцииФункция f(x) называется непрерывной в
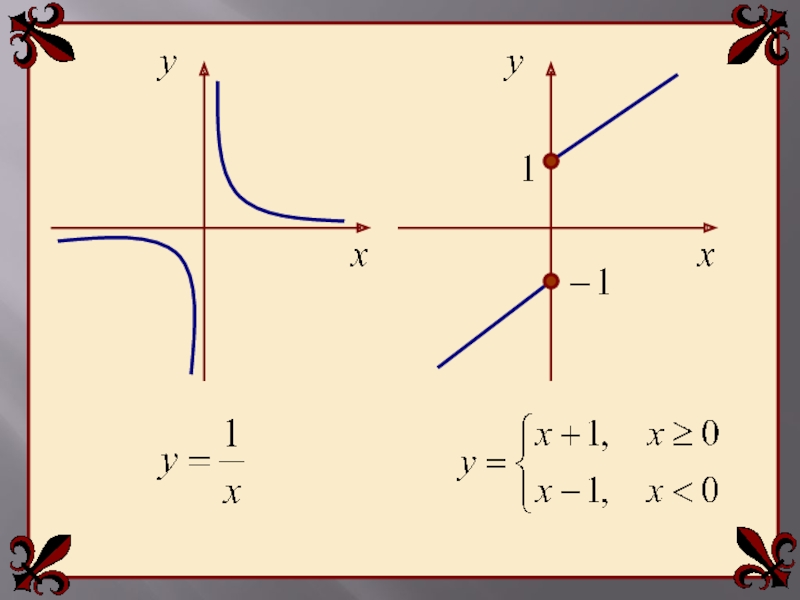
- 3. Функция не является непрерывной в точке х=0, т.к. не существует значения функции в этой точке:ПРИМЕРЫ.1
- 4. Функция существует в точке х=0 , т.к.
- 5. Функция является непрерывной в точке х=0, т.к. существует значение функции в этой точке: y(0)=03и существует предел
- 6. Определение непрерывности функции может быть записано в виде:определение 2.
- 7. Непрерывность функции в данной точке выражается непрерывностью
- 8. Слайд 8
- 9. определение 3.Функция f(x) называется непрерывной в точке
- 10. Точка x0 называется точкой разрыва функции f(x), если в этой точке функцияне является непрерывной.
- 11. Точка x0 называется точкой разрыва второгорода функции
- 12. Функция имеет точку разрыва второго рода х=0, поскольку: ПРИМЕРЫ.1
- 13. Функция 2имеет точку разрыва первого рода х=0, поскольку:
- 14. Слайд 14
Понятие непрерывностифункцииФункция f(x) называется непрерывной в точке x0, если она определена в этой точке (т.е. существует значениефункции в этой точке f(x0)) и имеет конечный предел при равный значению функции в этой точке:определение 1.
Слайд 2 Понятие непрерывности
функции
Функция f(x) называется непрерывной в точке x0, если она
определена в этой точке (т.е. существует значение
функции в этой точке f(x0)) и имеет конечный предел при
функции в этой точке f(x0)) и имеет конечный предел при
равный значению функции в этой точке:
определение 1.
Слайд 3Функция
не является непрерывной в точке х=0, т.к. не существует значения
функции в этой точке:
ПРИМЕРЫ.
1
Слайд 4Функция
существует в точке х=0 , т.к. у(0)=1
2
Рассмотрим пределы этой
функции в точке х=0 .
Предел слева:
Предел справа:
Эти пределы неравны, следовательно общего предела не существует и функция не является непрерывной в этой точке.
Слайд 5Функция
является непрерывной в точке х=0, т.к. существует значение функции в
этой точке: y(0)=0
3
и существует предел
Слайд 7Непрерывность функции в данной точке выражается непрерывностью графика при прохождении этой
точки.
Рассмотрим график функции y=f(x).
Дадим аргументу x0 приращение Δx. Тогда функция получит приращение Δy:
Графически:
Слайд 9определение 3.
Функция f(x) называется непрерывной в точке x0, если она определена
в точке x0 и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
Слайд 10Точка x0 называется точкой разрыва
функции f(x), если в этой точке
функция
не является непрерывной.
не является непрерывной.
Слайд 11Точка x0 называется точкой разрыва второго
рода функции f(x), если хотя бы
один из
односторонних пределов функции равен
бесконечности или не существует.
односторонних пределов функции равен
бесконечности или не существует.
Точка x0 называется точкой разрыва первого
рода функции f(x), если существуют
односторонние пределы функции слева и
справа при
Точки разрыва бывают 1 и 2 рода.
