- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Подготовка к ЕГЭ. Алгоритм нахождения отрезка в треугольнике
Содержание
- 1. Презентация по математике на тему Подготовка к ЕГЭ. Алгоритм нахождения отрезка в треугольнике
- 2. Найти отрезокв треугольникеИзвестны сторона и угол. Значит
- 3. Решение: ∆ ABС – прямоугольный.АВ = 26;
- 4. Задача 2. В треугольнике
- 5. Задача 3. В треугольнике АВС Решение.Треугольник АВС-произвольный
- 6. Задача 4. В треугольнике ABC АС = ВС
- 7. Задача 5. Основания равнобедренной трапеции равны 7
- 8. Задача 6. Найдите радиус окружности,
- 9. При использовании свойства трапеции: высота равнобедренной трапеции,
- 10. Задача 7. В прямоугольнике диагональ делит угол
- 11. Задача 8. Найдите высоту ромба, сторона которого
- 12. Слайд 12
- 13. ЛитератураЕГЭ 2012. Математика. Задача В6.Планиметрия:углы и длины.Рабочая
Слайд 1
Подготовка к ЕГЭ
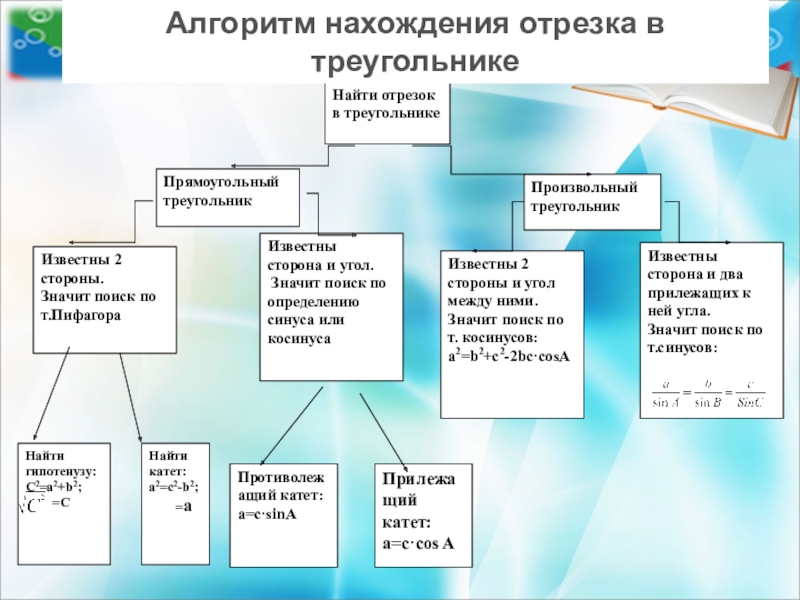
Алгоритм нахождения отрезка в треугольнике
Выполнила :
Слайд 2Найти отрезок
в треугольнике
Известны сторона и угол.
Значит поиск по определению синуса
Известны 2 стороны.
Значит поиск по т.Пифагора
Прямоугольный треугольник
Произвольный треугольник
Найти гипотенузу:
С2=a2+b2;
=C
Найти катет:
a2=c2-b2;
=a
Противолежащий катет:
a=c·sinA
Известны 2 стороны и угол между ними.
Значит поиск по т. косинусов:
a2=b2+c2-2bc·cosA
Известны сторона и два прилежащих к ней угла.
Значит поиск по т.синусов:
Прилежащий катет:
a=c·cos A
Алгоритм нахождения отрезка в треугольнике
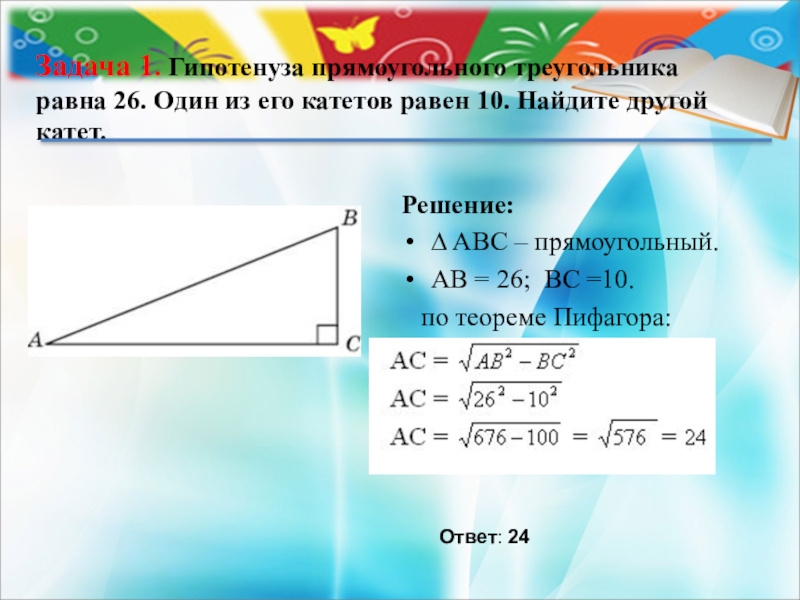
Слайд 3Решение:
∆ ABС – прямоугольный.
АВ = 26; ВС =10.
по
Задача 1. Гипотенуза прямоугольного треугольника равна 26. Один из его катетов равен 10. Найдите другой катет.
Ответ: 24
Слайд 4 Задача 2. В треугольнике ABC угол C прямой, BC=6, sinA=0,6. Найдите
Ответ: 10
6
?
Решение
∆ АВС – прямоугольный
Используем определение синуса : sinA=
AB= 10.
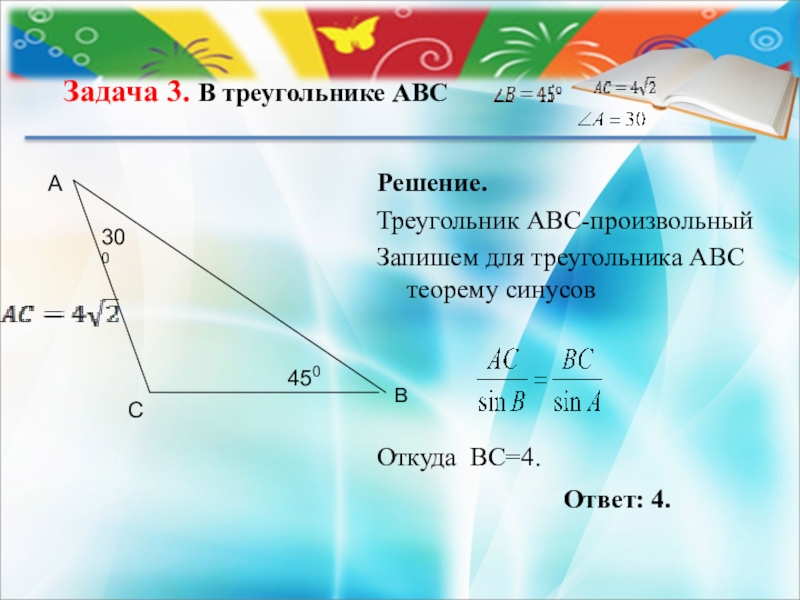
Слайд 5Задача 3. В треугольнике АВС
Решение.
Треугольник АВС-произвольный
Запишем для треугольника АВС
Откуда ВС=4.
Ответ: 4.
А
В
300
450
С
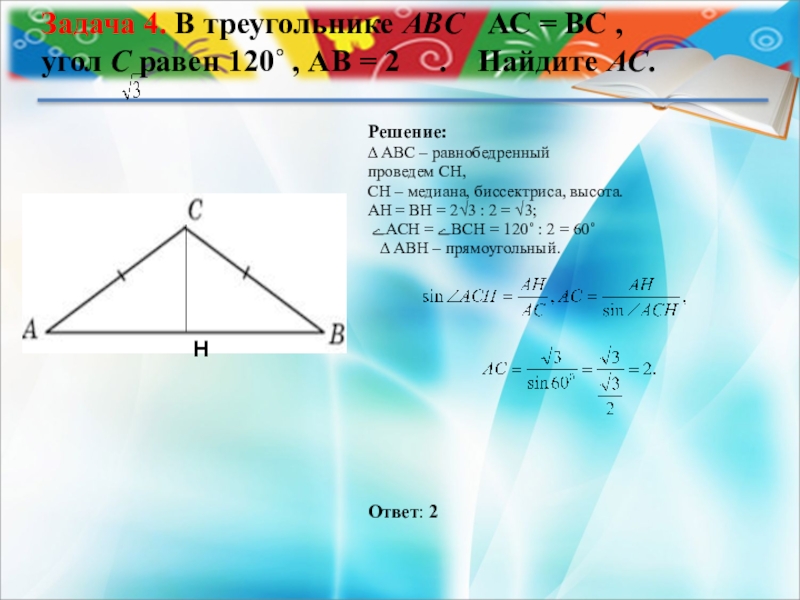
Слайд 6Задача 4. В треугольнике ABC АС = ВС , угол C равен 120˚ , АВ =
Решение:
∆ ABС – равнобедренный
проведем СН,
СН – медиана, биссектриса, высота.
АН = ВН = 2√3 : 2 = √3;
ےAСН = ےBСН = 120˚ : 2 = 60˚
∆ ABН – прямоугольный.
Ответ: 2
Н
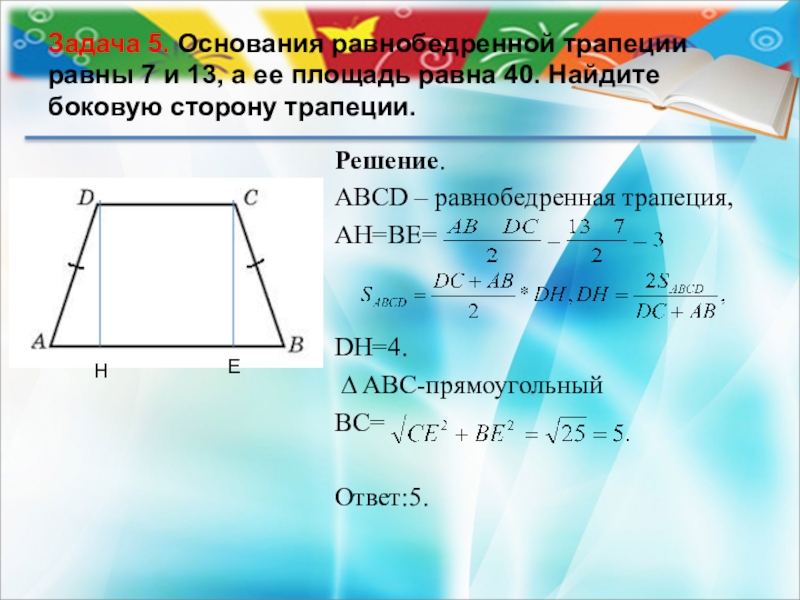
Слайд 7Задача 5. Основания равнобедренной трапеции равны 7 и 13, а ее
Решение.
АВСD – равнобедренная трапеция,
АН=ВЕ=
DH=4.
∆ ABC-прямоугольный
ВС=
Ответ:5.
Н
Е
Слайд 8
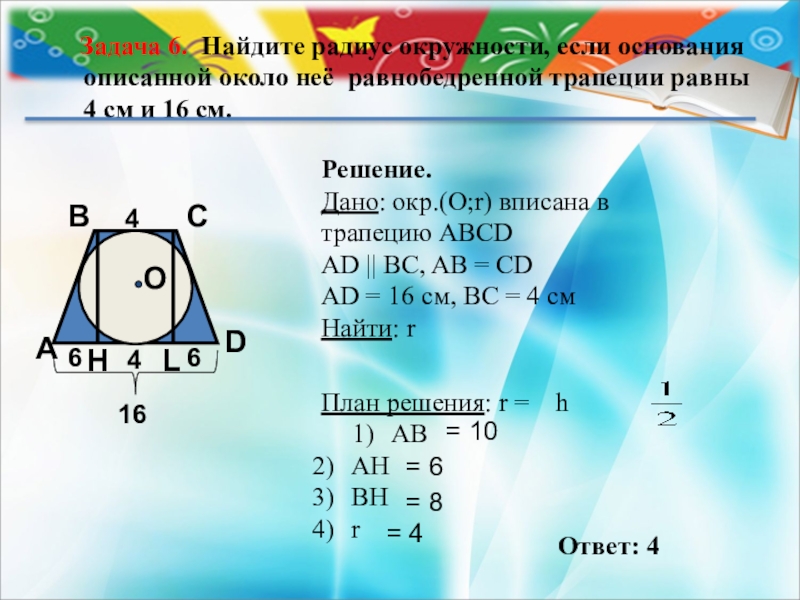
Задача 6. Найдите радиус окружности, если основания описанной около
B
A
D
С
4
4
6
6
16
Решение.
Дано: окр.(О;r) вписана в
трапецию ABCD
AD || BC, AB = CD
AD = 16 cм, ВС = 4 см
Найти: r
O
H
L
План решения: r = h
АВ
АН
ВН
r
= 10
= 6
= 8
= 4
Ответ: 4
Слайд 9При использовании свойства трапеции: высота равнобедренной трапеции, в которую можно вписать окружность,
Задачу 6 можно решить иначе:
4
16
A
O
B
C
D
Решение:
(cм)
h 2 = a ∙ b
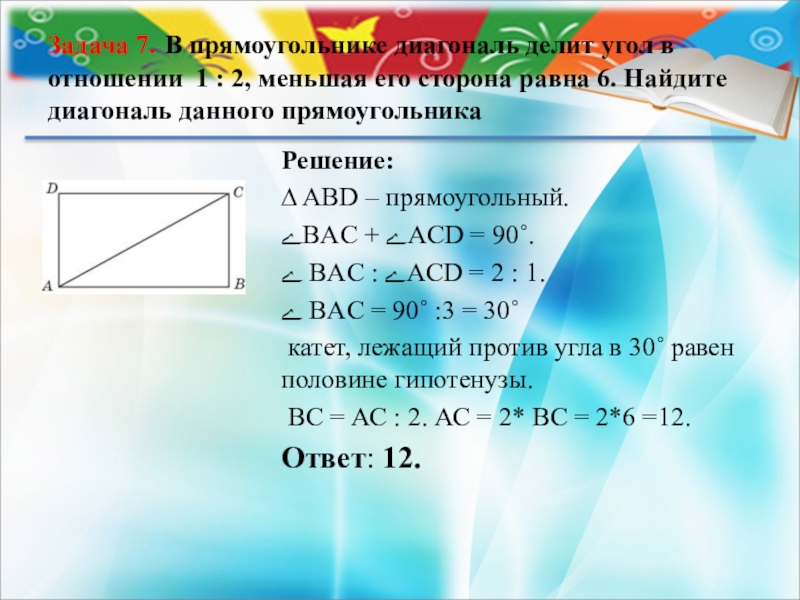
Слайд 10Задача 7. В прямоугольнике диагональ делит угол в отношении 1 :
Решение:
∆ ABD – прямоугольный.
ےBAС + ےAСD = 90˚.
ے BAС : ےAСD = 2 : 1.
ے BAС = 90˚ :3 = 30˚
катет, лежащий против угла в 30˚ равен половине гипотенузы.
ВС = АС : 2. АС = 2* ВС = 2*6 =12.
Ответ: 12.
Слайд 11Задача 8. Найдите высоту ромба, сторона которого равна √3 , а острый
Решение.
DH- высота,
∆ ADH – прямоугольный, используя алгоритм получим:
DH=
Ответ: 0,5.
√3
Слайд 13Литература
ЕГЭ 2012. Математика. Задача В6.Планиметрия:углы и длины.Рабочая тетрадь./Под ред. А.Л. Семенова
ЕГЭ. Математика. Решение задач типа В: универсальные материалы с методическими рекомендациями и ответами/Ю.А. Глазков, И.К. Варшавский, М,Я,Гаиашвили. - М.:Издательство»Экзамен».2012.397
http://reshuege.ru/test?theme=96
http://www.egetrener.ru/view_best.php?kritery=6 http://www.egetrener.ru/view_best.php?kritery=6 – видеоуроки.
Шаблон. Бондаренко Татьяна Николаевна, МОУ «НШ-ДС» г.Железноводска, заместитель директора по воспитательной работе, учитель начальных классов, Шаблон. Бондаренко Татьяна Николаевна, МОУ «НШ-ДС» г.Железноводска, заместитель директора по воспитательной работе, учитель начальных классов, http://pedsovet.su/