БойкоН.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Первообразная
Содержание
- 1. Презентация по математике на тему Первообразная
- 2. Три пути ведут к знанию: путь размышления
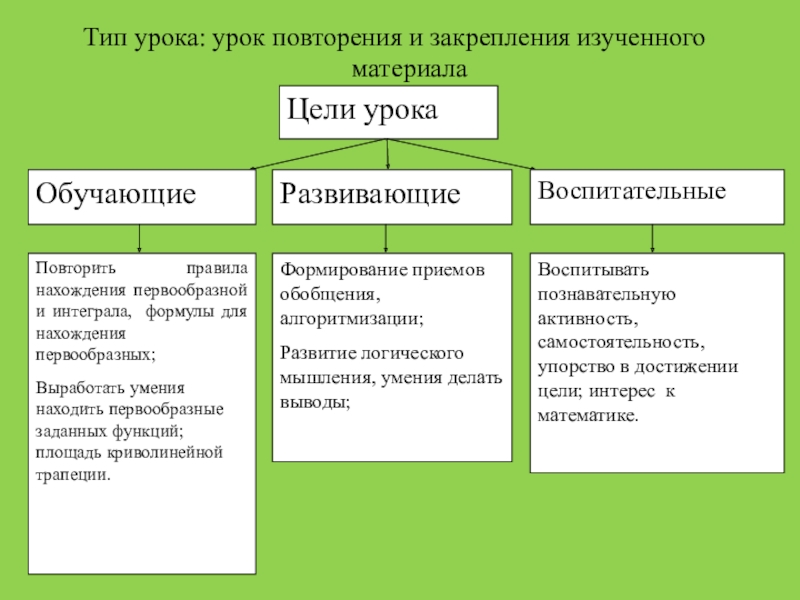
- 3. Тип урока: урок повторения и закрепления изученного материала
- 4. Блиц-опросОпределение первообразной.Основное свойство первообразных.Геометрический смысл основного свойства
- 5. Историческая справкаИстория понятия интеграла тесно связана с
- 6. Математический диктант с самопроверкой найдите первообразную1) f(x)=x;
- 7. Ответы:F(x)=F(x)=F(x) = - 7 x + cF(x)=
- 8. Связь между операциями интегрирования и дифференцированияПроизводная"Производит" новую функциюПервообразнаяПервичный образдифференцированиевычисление производнойинтегрированиевосстановление функции из производной
- 9. Три правила нахождения первообразных1) Если F(x) есть
- 10. Определенный интеграл– формула Ньютона-Лейбница.Геометрический смысл определенного интеграла
- 11. Вычисление объемов телПусть задано тело объемом V,
- 12. Применение интегралаКроме этого определенный интеграл используется для
- 13. Прилетела бабочка, Она вместо указкиПопытайтесь вслед за ней пробежаться глазками.
- 14. Вычислите площадь криволинейной трапеции, ограниченной линиями
- 15. Домашнее заданиеВычислите интегралыI Уровень1)
- 16. РефлексияНадо повторить ещё разСовсем не понятноВсё легко и просто
- 17. Спасибо за внимание!
Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта – это путь самый горький.Конфуций
Слайд 1Первообразная
МБОУ СШ № 1 с углубленным изучением отдельных предметов имени Ф.Г.Логинова
Учитель
Слайд 2Три пути ведут к знанию: путь размышления – это путь самый благородный, путь
подражания – это путь
самый легкий и
путь опыта – это путь
самый горький.
Конфуций
Конфуций
Слайд 4Блиц-опрос
Определение первообразной.
Основное свойство первообразных.
Геометрический смысл основного свойства первообразной?
Три правила нахождения первообразных.
Какую
фигуру называют криволинейной трапецией?
Формула для вычисления площади криволинейной трапеции.
Что такое интеграл?
Геометрический смысл интеграла?
Формула Ньютона- Лейбница.
Примеры применения определенного интеграла в геометрии и физике.
Какая связь существует между операциями дифференцирования и интегрирования?
Формула для вычисления площади криволинейной трапеции.
Что такое интеграл?
Геометрический смысл интеграла?
Формула Ньютона- Лейбница.
Примеры применения определенного интеграла в геометрии и физике.
Какая связь существует между операциями дифференцирования и интегрирования?
Слайд 5Историческая справка
История понятия интеграла тесно связана с задачами нахождения квадратур, т.е.
задачами на вычисление площадей. Вычислениями площадей поверхностей и объемов тел занимались еще математики Древней Греции и Рима. Первым европейским математиком, получившим новые формулы для площадей фигур и объемов тел, был знаменитый астроном И. Кеплер. После исследований ряда ученых (П.Ферма, Д.Валлиса) И. Барроу открыл связь между задачами отыскания площадей и проведением касательной (т.е. между интегрированием и дифференцированием). Исследование связи между этими операциями, свободное от геометрического языка, было дано И.Ньютоном и Г. Лейбницем.
Современное обозначение интеграла восходит к Лейбницу, у которого оно выражало мысль, что площадь криволинейной трапеции есть сумма площадей бесконечно тонких полосок шириной d и высоты f(x). Сам знак интеграла является стилизованной латинской буквой S (summa). Символ интеграла введен с 1675г., а вопросами интегрального исчисления занимаются с 1696г. Хотя интеграл изучают, в основном, ученые–математики, но и физики внесли свой вклад в эту науку. Практически ни одна формула физики не обходится без
дифференциального и интегрального исчислений.
Современное обозначение интеграла восходит к Лейбницу, у которого оно выражало мысль, что площадь криволинейной трапеции есть сумма площадей бесконечно тонких полосок шириной d и высоты f(x). Сам знак интеграла является стилизованной латинской буквой S (summa). Символ интеграла введен с 1675г., а вопросами интегрального исчисления занимаются с 1696г. Хотя интеграл изучают, в основном, ученые–математики, но и физики внесли свой вклад в эту науку. Практически ни одна формула физики не обходится без
дифференциального и интегрального исчислений.
Слайд 6Математический диктант с самопроверкой
найдите первообразную
1) f(x)=x; F(x)-?
2) f(x)= ;
F(x)-?
3) f(x)= - 7; F(x)-?
4) f(x)=5 sin(x); F(x)-?
5) f(x)=3 cos(3x); F(x)-?
6)f(x)=3 - 4x; F(x)-?
3) f(x)= - 7; F(x)-?
4) f(x)=5 sin(x); F(x)-?
5) f(x)=3 cos(3x); F(x)-?
6)f(x)=3 - 4x; F(x)-?
Слайд 8Связь между операциями интегрирования и дифференцирования
Производная
"Производит" новую функцию
Первообразная
Первичный образ
дифференцирование
вычисление производной
интегрирование
восстановление функции
из производной
Слайд 9Три правила нахождения первообразных
1) Если F(x) есть первообразная для f(x), а
G(x) –
первообразная для g(x), то F(x) + G(x) есть
первообразная для f(x) + g(x).
первообразная для g(x), то F(x) + G(x) есть
первообразная для f(x) + g(x).
2) Если F(x) есть первообразная для f(x), а k –
постоянная, то функция kF(x) есть первообразная
для kf.
3) Если F(x) есть первообразная для f(x), а k и b –
постоянные, причем k ≠ 0, то функция F(kx + b)
есть первообразная для f(kx + b).
Слайд 10Определенный интеграл
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла заключается в том, что
определенный интеграл равен площади криволинейной трапеции, образованной линиями:
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.
Слайд 11Вычисление объемов тел
Пусть задано тело объемом V, причем имеется такая прямая,
что, какую бы плоскость, перпендикулярную этой прямой, мы ни взяли, нам известна площадь S сечения тела этой плоскостью. Но плоскость, перпендикулярная оси Ох, пересекает ее в некоторой точке х. Следовательно, каждому числу х (из отрезка [а; b]) поставлено в соответствие единственное число S (х) — площадь сечения тела этой плоскостью. Тем самым на отрезке [а; b] задана функция S(x). Если функция S непрерывна на отрезке [а; b] то справедлива формула:
Слайд 12Применение интеграла
Кроме этого определенный интеграл используется для вычисления площадей плоских фигур,
объемов тел вращения, длин дуг кривых.