- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Параллельность в пространстве
Содержание
- 1. Презентация по математике на тему Параллельность в пространстве
- 2. Устная работа.АВСДА1В1С1Д1αДано: куб АВСДА1В1С1Д1Найдите:Несколько точек, которые лежат
- 3. Параллельные прямые в пространстве1Каково может быть взаимное
- 4. Параллельные прямые в пространствеПараллельными прямыми в пространстве
- 5. Так как две прямые в пространстве называются
- 6. Теорема о параллельных прямых Через
- 7. Параллельные прямые в пространствеДан куб. Являются ли
- 8. Параллельные прямые в пространствеДве прямые называются скрещивающимися,
- 9. Признак скрещивающихся прямыхЕсли b є α, a
- 10. Найти:3 пары параллельных прямых, 3 пары скрещивающихся
- 11. Параллельные прямые в пространствеПо рисункам назовите:1) пары скрещивающихся ребер;2) пары параллельных ребер.DCABKLNK1L1N1
- 12. Параллельные прямые в пространствеАлгоритм распознавания взаимного расположения
- 13. ЛеммаДано: a ΙΙ b, Если a ∩ α,то b∩α
- 14. Теорема
- 15. Слайд 15
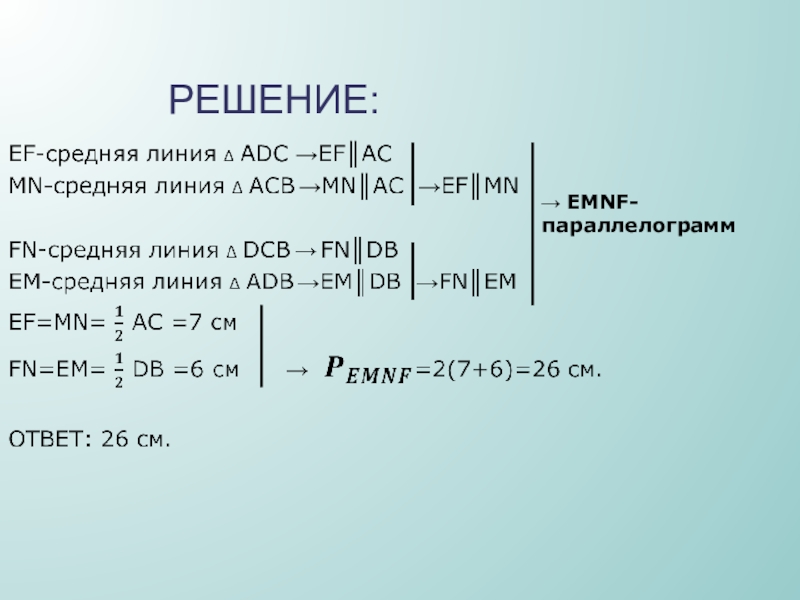
- 16. РЕШЕНИЕ:→ EMNF-параллелограмм
- 17. Параллельные прямые в пространстве1Всегда ли две непересекающиеся
- 18. Параллельность прямой и плоскости в пространстве
- 19. Параллельность прямой и плоскости Возможны три случая взаимного расположения прямой и плоскости в пространстве:
- 20. 1. Если прямая и плоскость имеют одну общую точку, то прямая пересекает эту плоскость.
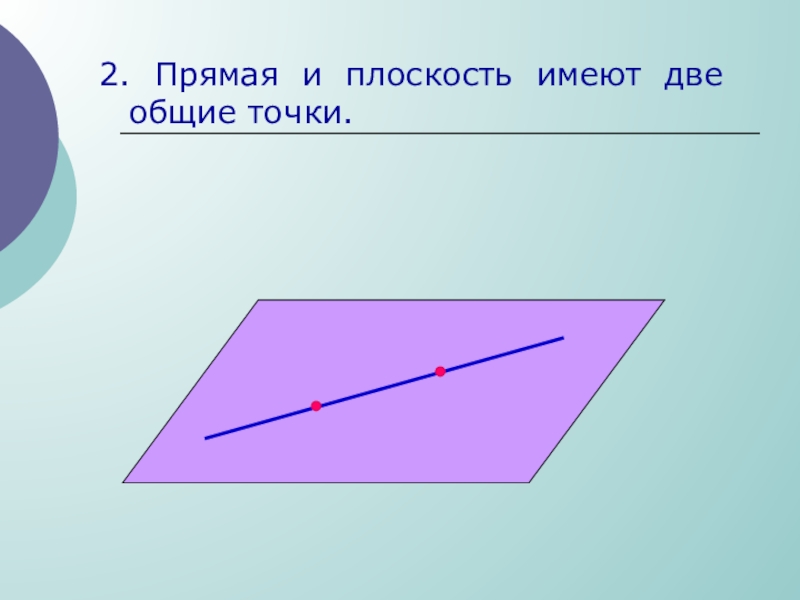
- 21. 2. Прямая и плоскость имеют две общие точки.
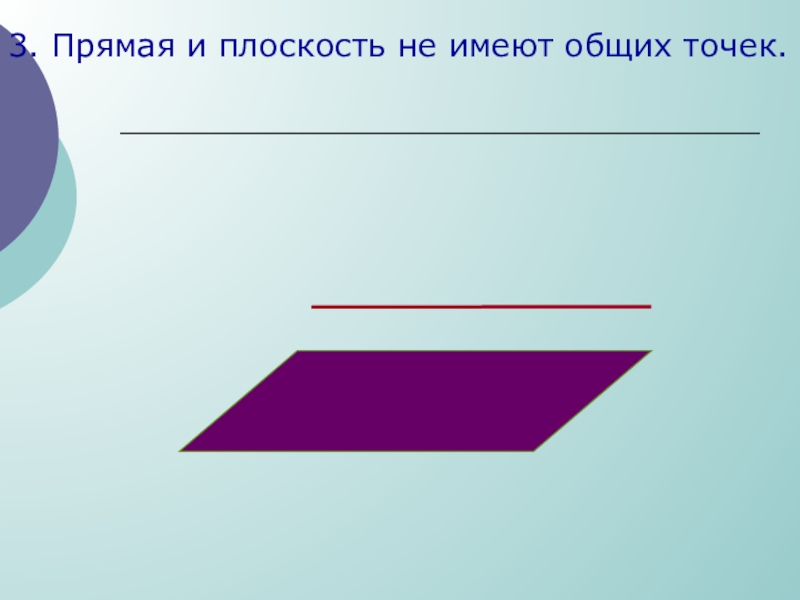
- 22. 3. Прямая и плоскость не имеют общих точек.
- 23. Слайд 23
- 24. Признак параллельности двух прямых. Если прямая, лежащая
- 25. Слайд 25
- 26. Параллельность прямой и плоскости (устно)E и F
- 27. Слайд 27
- 28. Слайд 28
- 29. ЗАДАЧАДано: Δ АВС ,АС//αАС = 10 смАВ
- 30. ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
- 31. Слайд 31
- 32. Слайд 32
- 33. Признак параллельности двух плоскостей.
- 34. Слайд 34
- 35. 2. Отрезки параллельных прямых, заключенные между параллельными
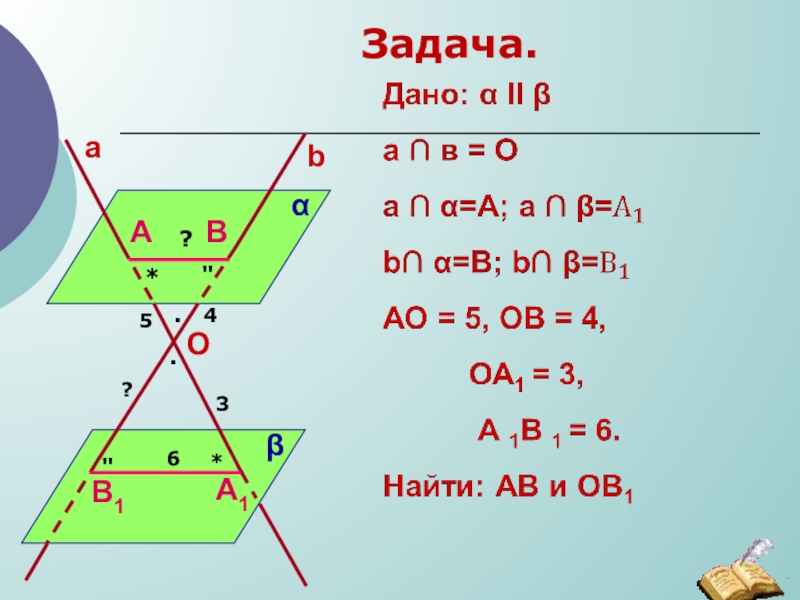
- 36. Задача.5436??..**""
- 37. ЗАДАЧАДано:∆ АВС
- 38. ЗАДАЧААВСDЕКРαβДано:∆ АВС
- 39. Используемая литература:1. Геометрия: Учебник для средней школы.
Слайд 2Устная работа.
А
В
С
Д
А1
В1
С1
Д1
α
Дано: куб АВСДА1В1С1Д1
Найдите:
Несколько точек, которые лежат в плоскости α;
Несколько точек,
Несколько прямых, которые лежат в плоскости α;
Несколько прямых, которые не лежат в плоскости α;
Несколько прямых которые пересекают прямую ВС;
Несколько прямых, которые не пересекают прямую ВС.
Слайд 3Параллельные прямые в пространстве
1
Каково может быть взаимное расположение двух прямых на
(совпадают, пересекаются, параллельны)
2
Дайте определение параллельных прямых на плоскости.
Параллельными называются прямые, не имеющие общих точек.
Слайд 4Параллельные прямые в пространстве
Параллельными прямыми в пространстве называются прямые, которые лежат
Определение
Слайд 5Так как две прямые в пространстве называются параллельными, если они не
Значит, через две параллельные прямые можно провести плоскость и только одну.
a
b
a ΙΙ b
Слайд 6Теорема о параллельных прямых
Через любую точку
Если даны пр. a,
M є a ,
то :
1. через пр. a можно
провести пр. b ΙΙ a.
2. пр. b -единственная
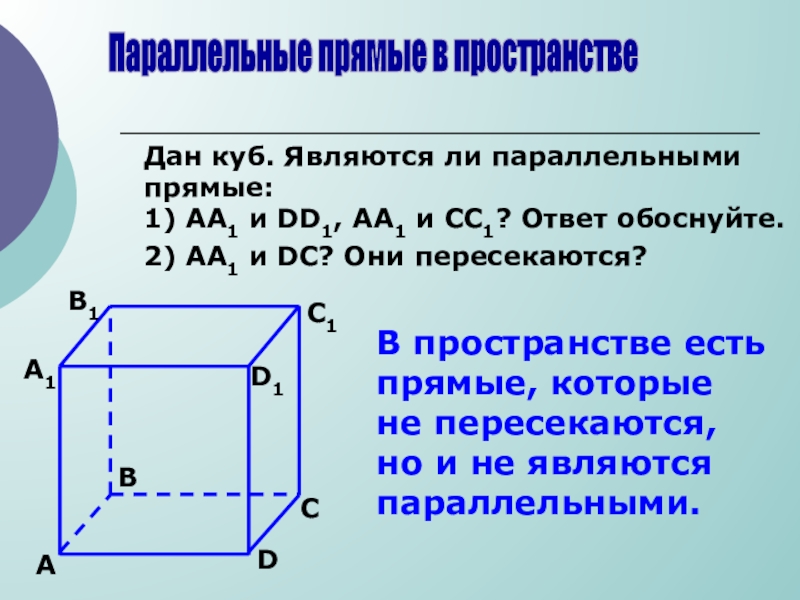
Слайд 7Параллельные прямые в пространстве
Дан куб. Являются ли параллельными прямые:
D
C
A
B
D1
C1
A1
B1
1) АА1 и
2) АА1 и DС? Они пересекаются?
В пространстве есть прямые, которые не пересекаются, но и не являются параллельными.
Слайд 8Параллельные прямые в пространстве
Две прямые называются скрещивающимися, если они не лежат
Слайд 10Найти:
3 пары параллельных прямых,
3 пары скрещивающихся прямых,
3 пары пересекающихся прямых.
Пересекаются
B1D и BC?
B1D и A1C1?
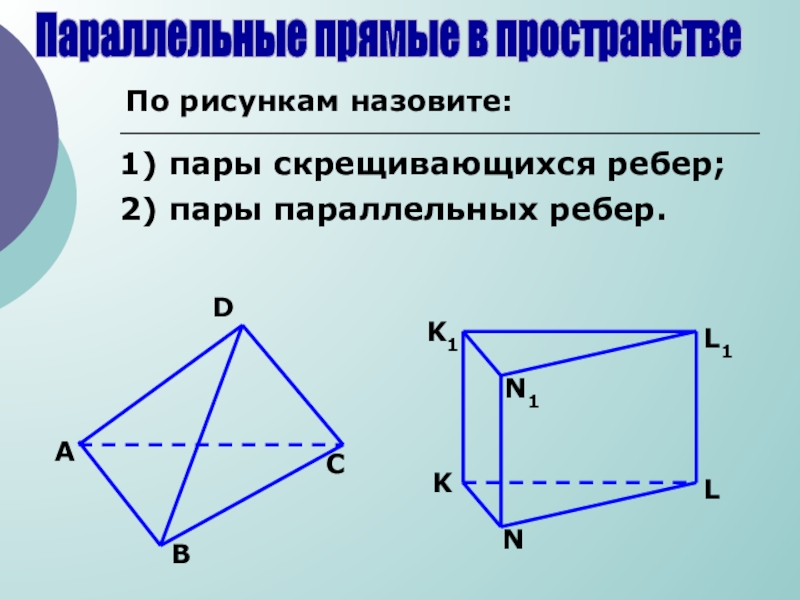
Слайд 11Параллельные прямые в пространстве
По рисункам назовите:
1) пары скрещивающихся ребер;
2) пары параллельных
D
C
A
B
K
L
N
K1
L1
N1
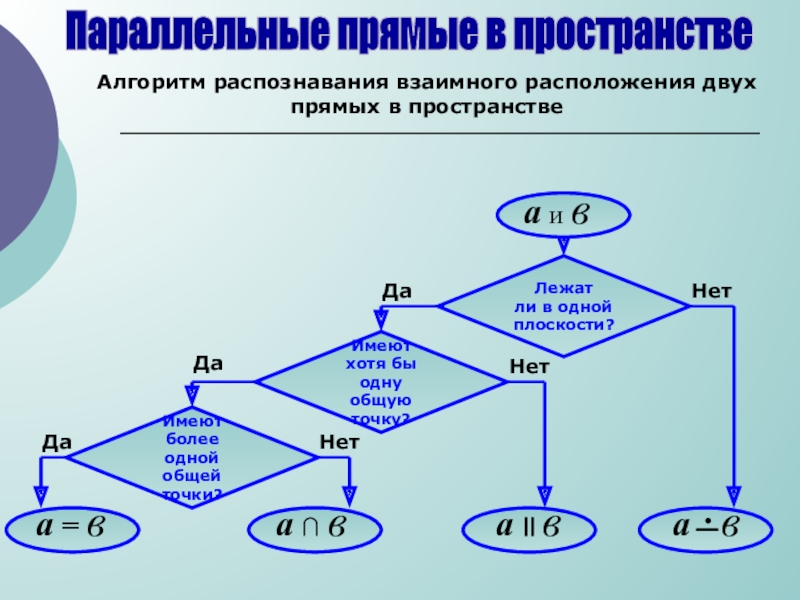
Слайд 12Параллельные прямые в пространстве
Алгоритм распознавания взаимного расположения двух прямых в пространстве
Лежат
ли
плоскости?
Имеют
хотя бы одну
общую
точку?
Имеют
более одной
общей
точки?
а и в
а = в
а в
а в
а в
Да
Да
Да
Нет
Нет
Нет
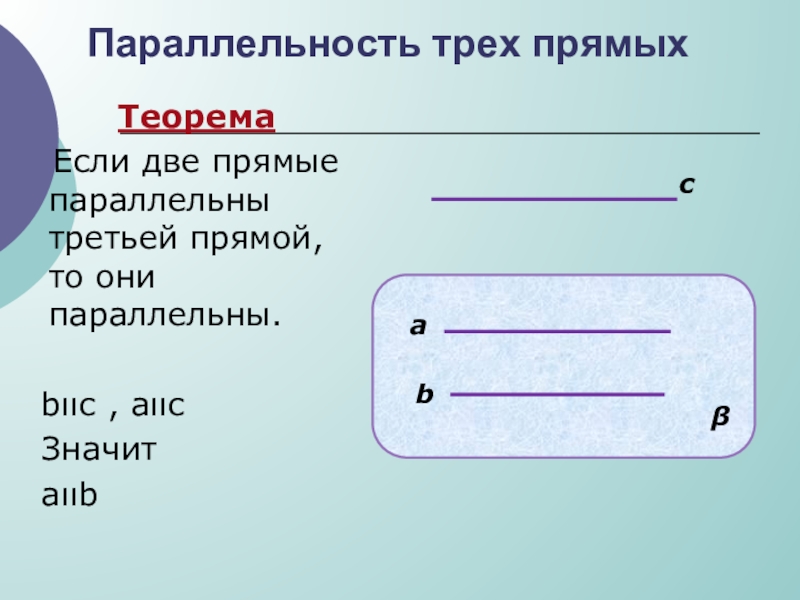
Слайд 14 Теорема
Если две прямые параллельны
bιιс , аιιс
Значит
аιιb
Параллельность трех прямых
с
а
b
β
Слайд 15
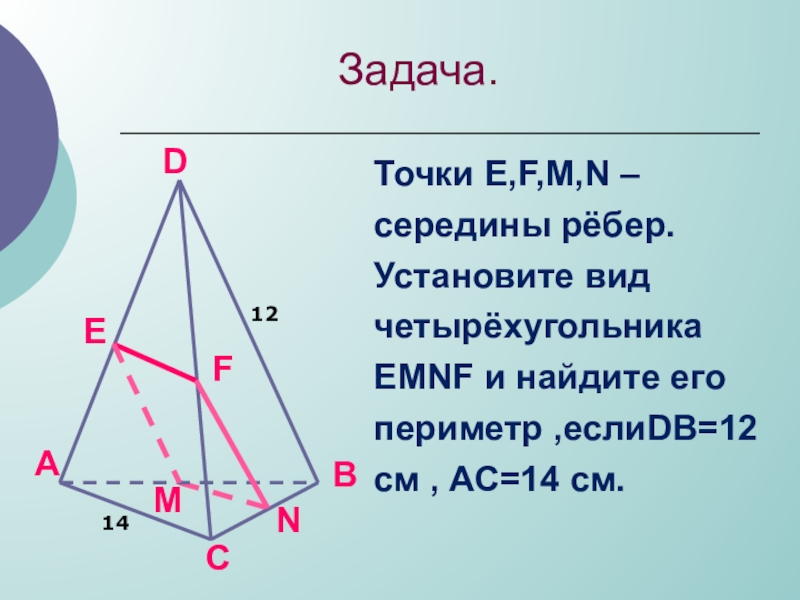
Точки Е,F,M,N – середины рёбер.Установите вид четырёхугольника ЕМNF и найдите его периметр ,еслиDB=12 см , АС=14 см.
12
14
Слайд 17Параллельные прямые в пространстве
1
Всегда ли две непересекающиеся прямые в пространстве параллельны?
2
Какие
3
4
Сколько можно провести в пространстве прямых, проходящих через данную точку, параллельных данной прямой?
Какие прямые называются скрещивающимися?
Слайд 19Параллельность прямой и плоскости
Возможны три случая взаимного расположения прямой
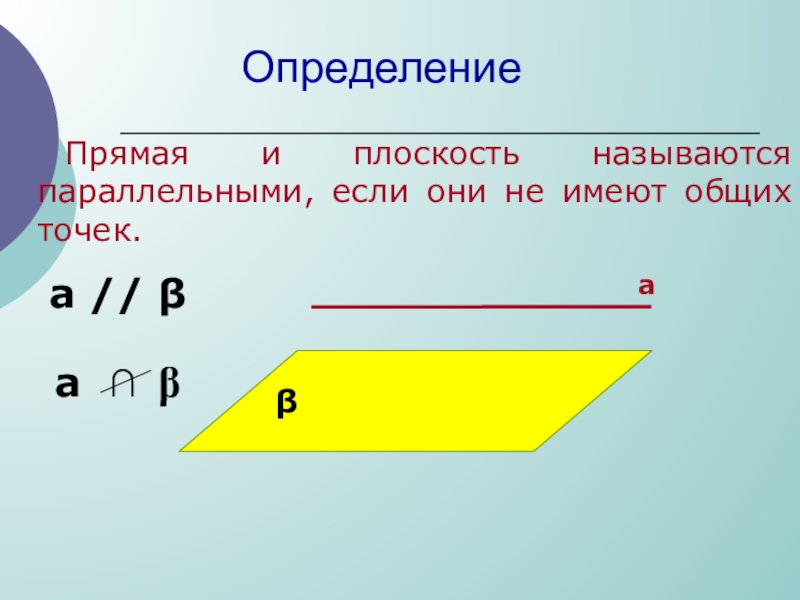
Слайд 23 Определение
β
а
а ∩ β
а // β
Слайд 24Признак параллельности двух прямых. Если прямая, лежащая в одной из пересекающихся плоскостей,
Если aєα, allβ, α ∩ β = c, то
allc
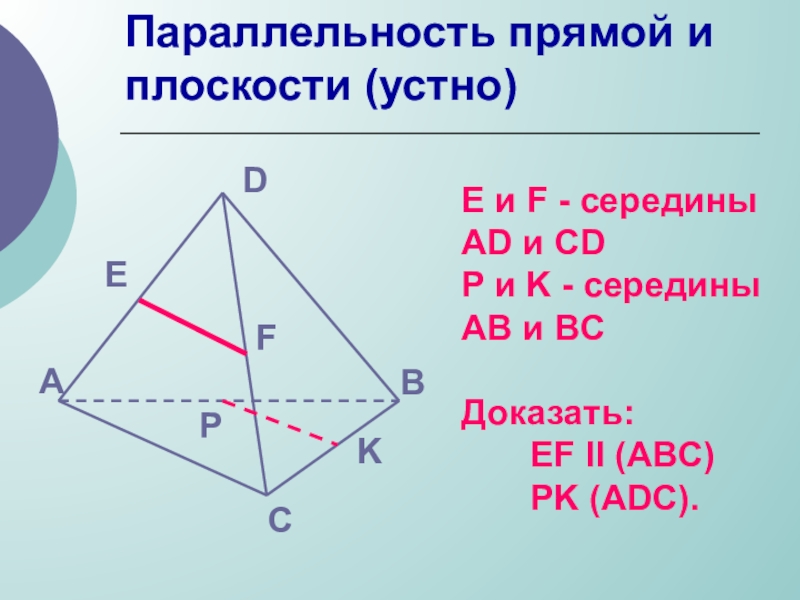
Слайд 26Параллельность прямой и плоскости (устно)
E и F - середины AD и
P и K - середины AB и BC
Доказать:
EF ll (ABC)
PK (ADC).
A
B
C
D
E
F
K
P
Слайд 27
Средняя линия трапеции лежит в некоторой плоскости. Докажите, что основания трапеции параллельны данной плоскости.
Слайд 33Признак параллельности двух плоскостей.
Пусть
пл-ти α и β,
a ∩ b, a1∩b1,
a , b є α,
a1 , b1 є β,
Если а// a1 ; b // b1 ,то α II β
Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то плоскости параллельны.
Слайд 34 Свойства.__________
1.
Если α II β, γ ∩ α = a,
γ ∩ β = b,
то a II b
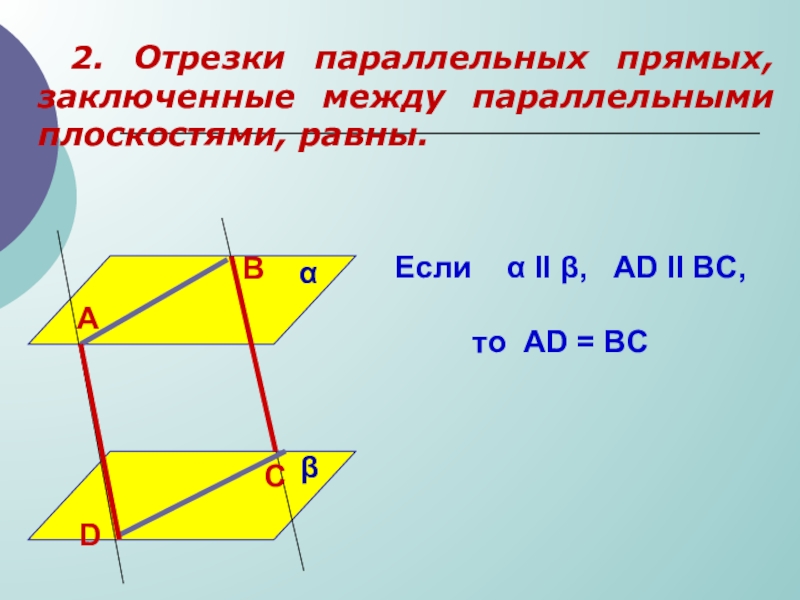
Слайд 352. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Если α
то AD = BC
α
β
А
B
C
D
Слайд 38 ЗАДАЧА
А
В
С
D
Е
К
Р
α
β
Дано:
∆ АВС ; α // β
АВ
ВС ∩ α=К;ВС ∩ β=Р
ВD:ВЕ=2:3
ВК=4см
Найти: ВР и ВЕ
4
Слайд 39Используемая литература:
1. Геометрия: Учебник для средней школы. 10–11 классы./ Под ред.
2. Геометрия. 10 класс. Поурочные планы / Авт.-сост. Г.И. Ковалева – Волгоград: Учитель, 2004
Презентацию подготовила:
Седова Оксана Михайловна
преподаватель математики
ГАОУ МО СПО «Печенгский политехнический техникум»
2016 год
Параллельные прямые в пространстве