«Чебаркульский профессиональный
техникум: Пуртова Т.И.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Параллелепипед, тетраэдр. Построение сечений (СПО)
Содержание
- 1. Презентация по математике на тему Параллелепипед, тетраэдр. Построение сечений (СПО)
- 2. ГЕОМЕТРИЯ – ЭТО ИСКУССТВО ПРАВИЛЬНО РАССУЖДАТЬ НА
- 3. План:1.Паралелепипед и его свойства2.Свойства тетраэдра3.Построение сечений многогранников4.Вопросы на повторение
- 4. ЦЕЛЬ:Ознакомиться с такими многогранниками как тетраэдр и
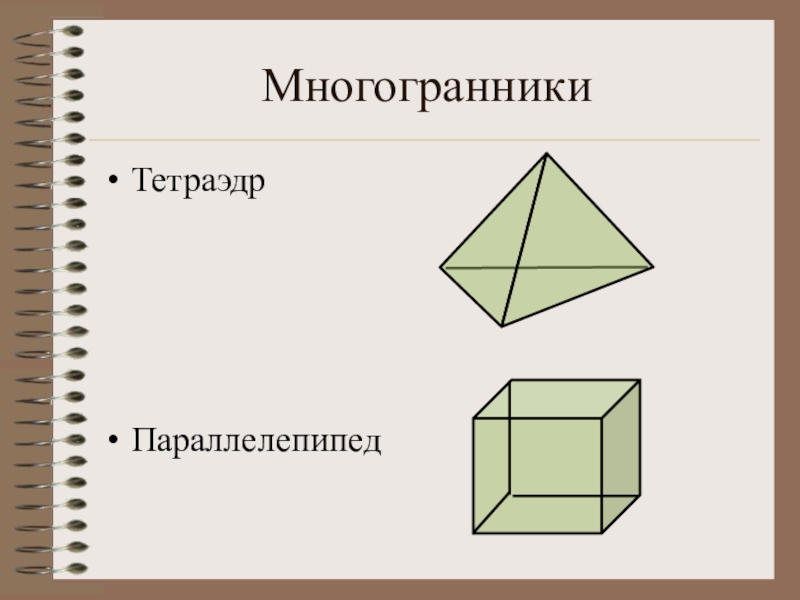
- 5. МногогранникиТетраэдрПараллелепипед
- 6. параллелепипед
- 7. Параллелепипед - это призма, основанием которой служит параллелограмм.
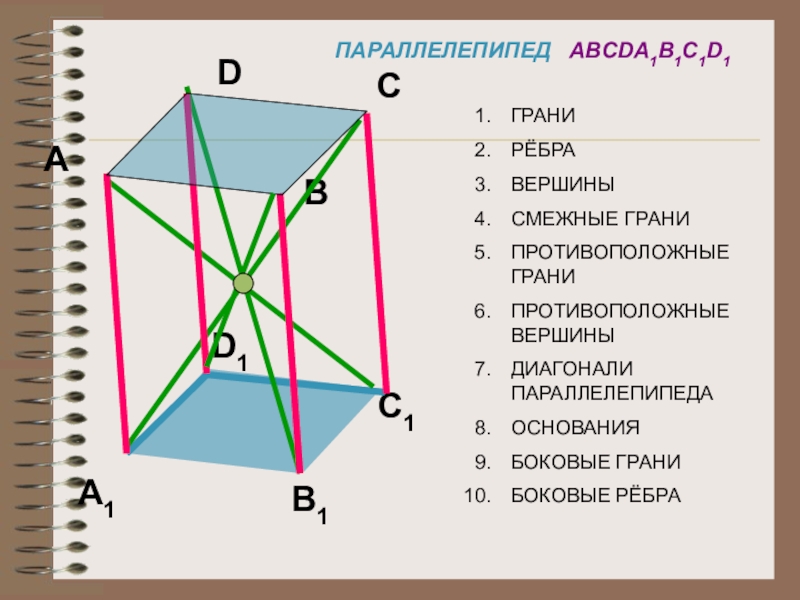
- 8. ПАРАЛЛЕЛЕПИПЕД ABCDA1B1C1D1ГРАНИРЁБРАВЕРШИНЫСМЕЖНЫЕ ГРАНИПРОТИВОПОЛОЖНЫЕ ГРАНИПРОТИВОПОЛОЖНЫЕ ВЕРШИНЫДИАГОНАЛИ ПАРАЛЛЕЛЕПИПЕДАОСНОВАНИЯБОКОВЫЕ ГРАНИБОКОВЫЕ РЁБРА
- 9. Свойства параллелепипеда10 Противоположные грани параллелепипеда равны.20 Диагонали параллелепипеда пересекаются и делятся точкой пересечения пополам.
- 10. Параллелепипед в жизни
- 11. тетраэдр
- 12. Тетраэдр, или треугольная пирамида,-простейший из многогранников,
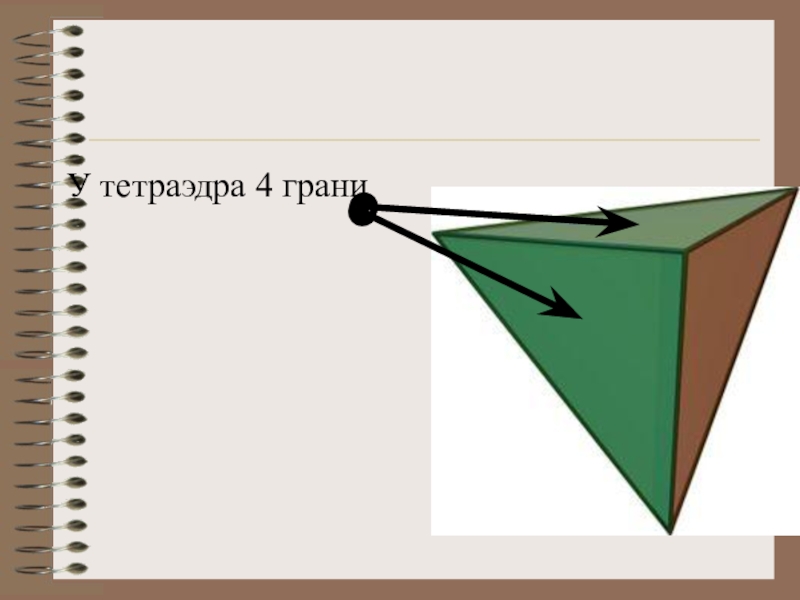
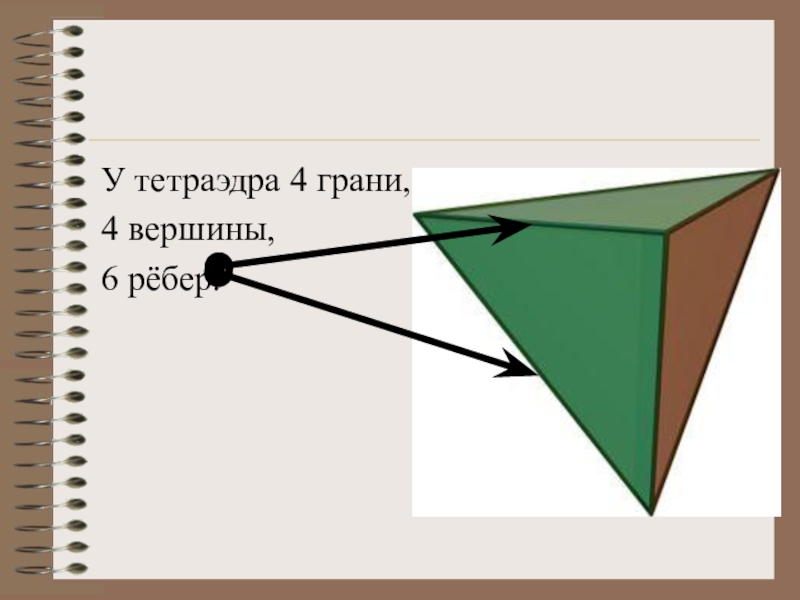
- 13. У тетраэдра 4 грани
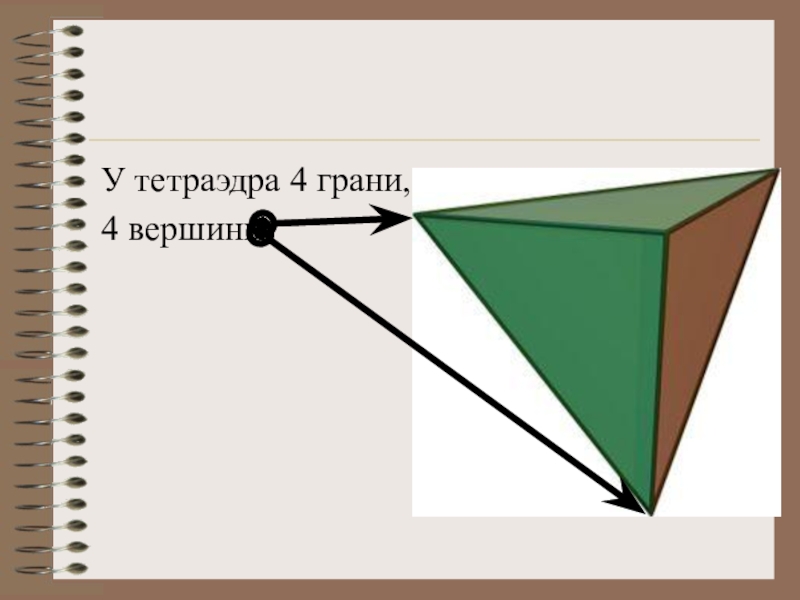
- 14. У тетраэдра 4 грани, 4 вершины
- 15. У тетраэдра 4 грани,4 вершины,6 рёбер.
- 16. Свойства тетраэдра:В тетраэдр можно вписать октаэдр, притом
- 17. Тетраэдр в жизни
- 18. Сечения параллелепипеда и тетраэдра
- 19. Сечением пространственного тела (например, многогранника) называется фигура,
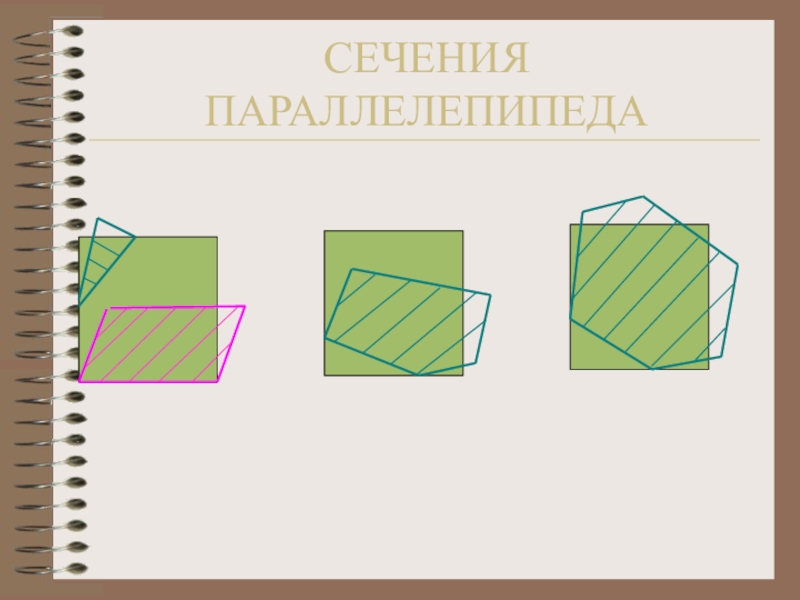
- 20. СЕЧЕНИЯ ПАРАЛЛЕЛЕПИПЕДА
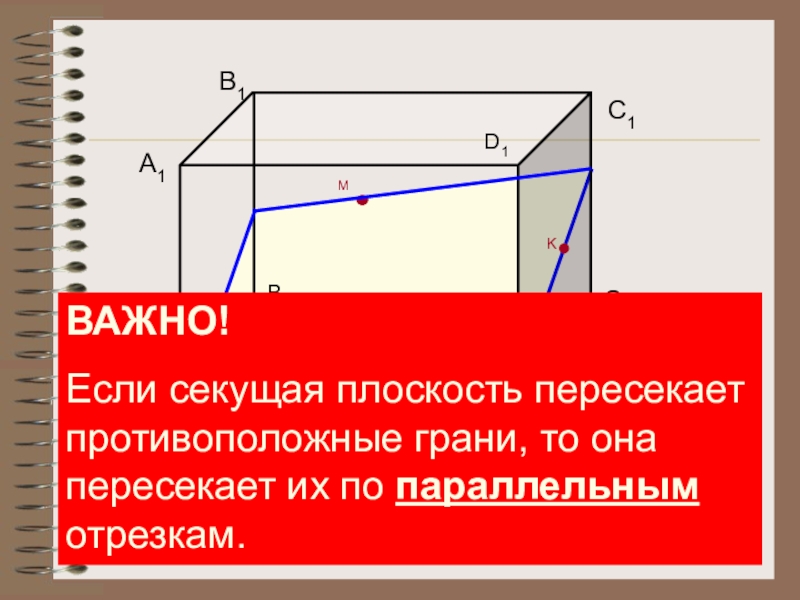
- 21. ABСB1D1DKMC1A1ВАЖНО!Если секущая плоскость пересекает противоположные грани, то она пересекает их по параллельным отрезкам.
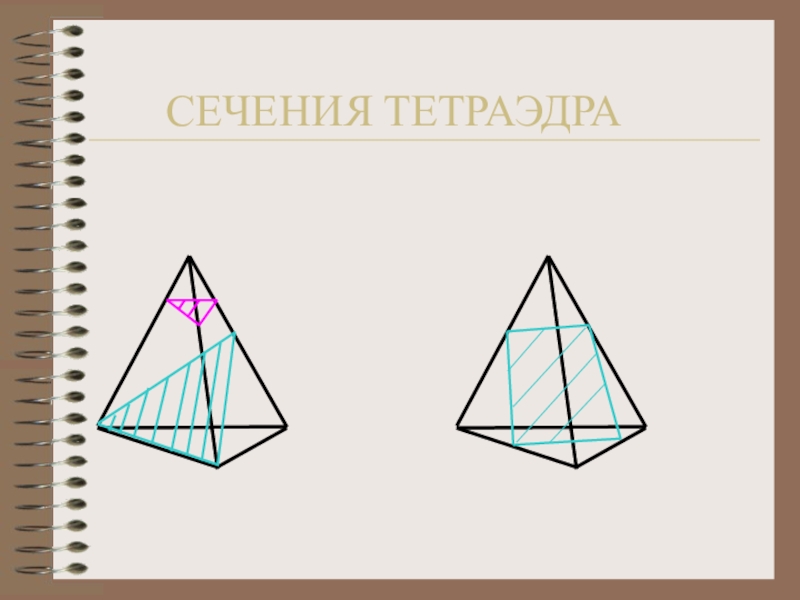
- 22. СЕЧЕНИЯ ТЕТРАЭДРА
- 23. Задания на повторение.
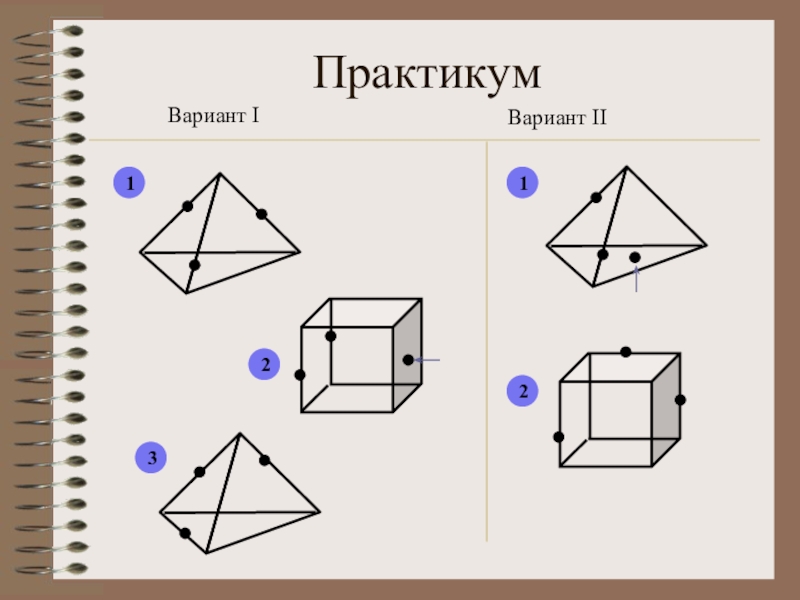
- 24. ПрактикумВариант IВариант II 12312
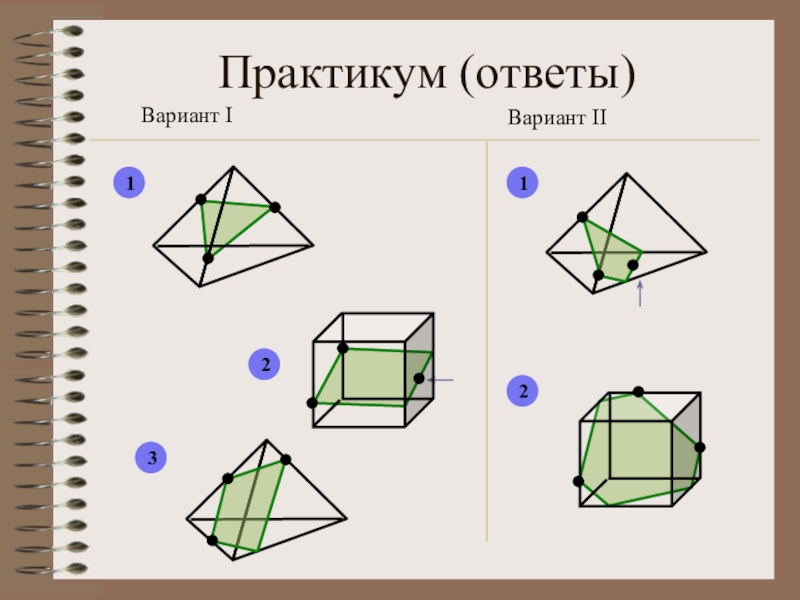
- 25. Практикум (ответы)Вариант I Вариант II 12312
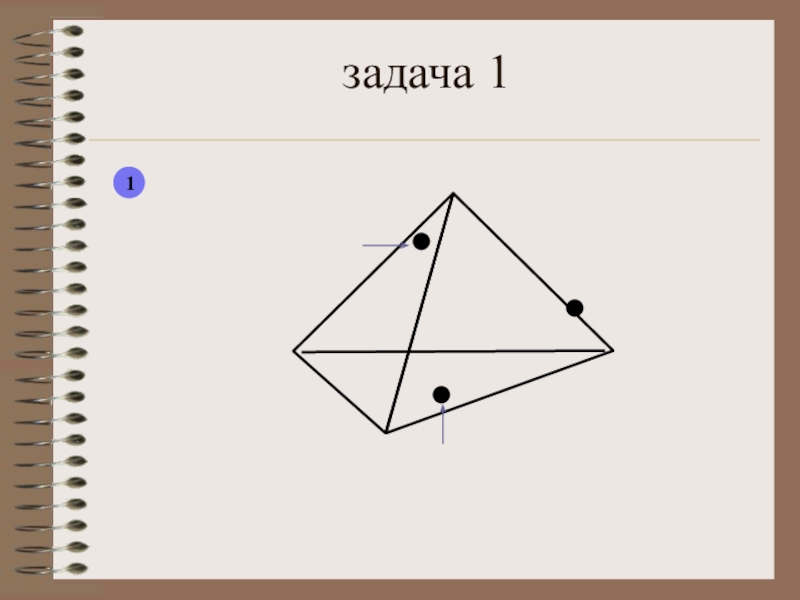
- 26. задача 11
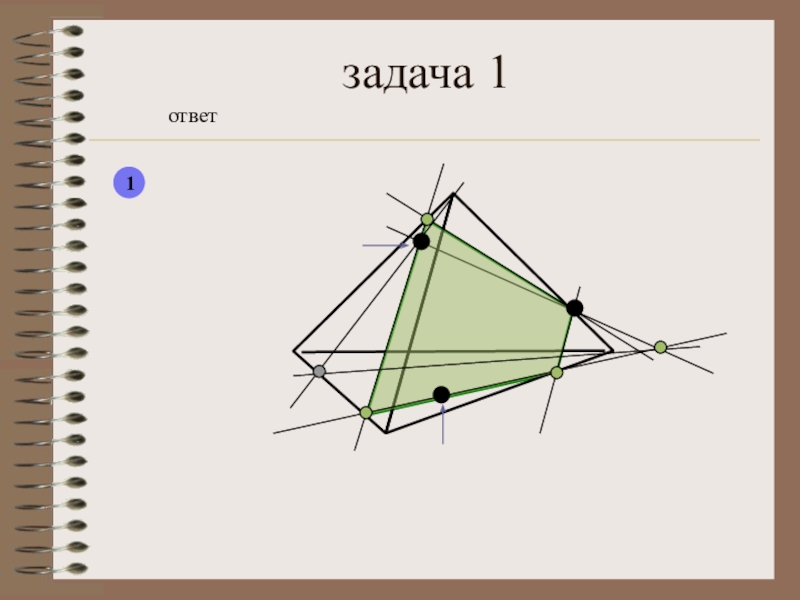
- 27. задача 1ответ1
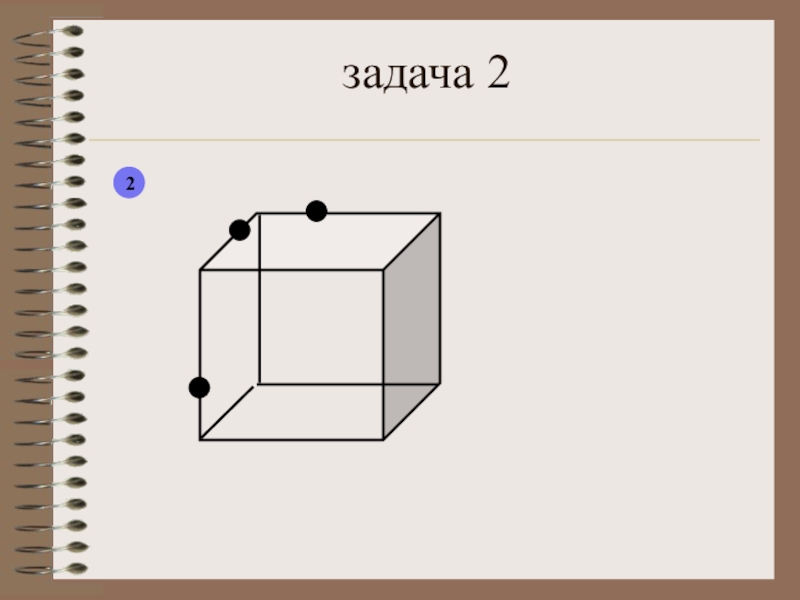
- 28. задача 22
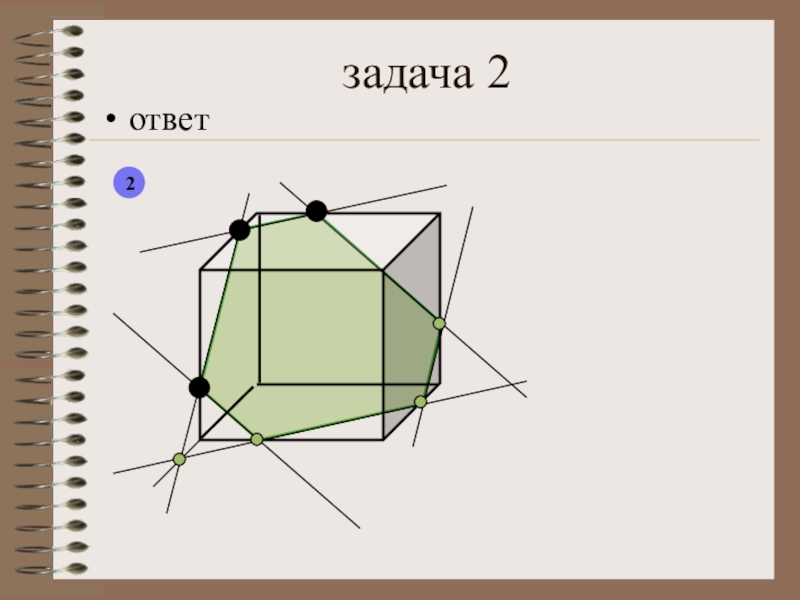
- 29. задача 22ответ
ГЕОМЕТРИЯ – ЭТО ИСКУССТВО ПРАВИЛЬНО РАССУЖДАТЬ НА НЕПРАВИЛЬНЫХ ЧЕРТЕЖАХ. ПОЙА Д.
Слайд 1Презентация по математике на тему: Параллелепипед и тетраэдр
Выполнила преподаватель математики
ГБПОУ
Слайд 3План:
1.Паралелепипед и его свойства
2.Свойства тетраэдра
3.Построение сечений многогранников
4.Вопросы на повторение
Слайд 4ЦЕЛЬ:
Ознакомиться с такими многогранниками как тетраэдр и параллелепипед.
рассмотреть общие принципы построения
сечений многогранников.
Выработать навыки решения задач на построение сечений тетраэдра и параллелепипеда.
Выработать навыки решения задач на построение сечений тетраэдра и параллелепипеда.
Слайд 8
ПАРАЛЛЕЛЕПИПЕД ABCDA1B1C1D1
ГРАНИ
РЁБРА
ВЕРШИНЫ
СМЕЖНЫЕ ГРАНИ
ПРОТИВОПОЛОЖНЫЕ ГРАНИ
ПРОТИВОПОЛОЖНЫЕ ВЕРШИНЫ
ДИАГОНАЛИ ПАРАЛЛЕЛЕПИПЕДА
ОСНОВАНИЯ
БОКОВЫЕ ГРАНИ
БОКОВЫЕ РЁБРА
Слайд 9Свойства параллелепипеда
10 Противоположные грани параллелепипеда равны.
20 Диагонали параллелепипеда пересекаются
и делятся точкой пересечения пополам.
Слайд 12 Тетраэдр, или треугольная пирамида,-простейший из многогранников, подобно тому как треугольник-
простейший из многоугольников на плоскости. Слово «тетраэдр» образовано из двух греческих слов: tetra- «четыре» и hedra- «основание», «грань».
Слайд 16Свойства тетраэдра:
В тетраэдр можно вписать октаэдр, притом четыре (из восьми) грани
октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.
Тетраэдр с ребром х состоит из одного вписанного октаэдра (в центре) с ребром х/2 и четырёх тетраэдров (по вершинам) с ребром х/2.
Тетраэдр можно вписать в куб двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба.
Тетраэдр можно вписать в икосаэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Тетраэдр с ребром х состоит из одного вписанного октаэдра (в центре) с ребром х/2 и четырёх тетраэдров (по вершинам) с ребром х/2.
Тетраэдр можно вписать в куб двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба.
Тетраэдр можно вписать в икосаэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Слайд 19Сечением пространственного тела (например, многогранника) называется фигура, получающаяся в пересечении тела
с плоскостью
Сечение тетраэдра и параллелепипеда – это выпуклый плоский многоугольник, вершины которого являются точками пересечения секущей плоскости с ребрами, а стороны – с его гранями
Сечение тетраэдра и параллелепипеда – это выпуклый плоский многоугольник, вершины которого являются точками пересечения секущей плоскости с ребрами, а стороны – с его гранями
ОПРЕДЕЛЕНИЕ
Слайд 21
A
B
С
B1
D1
D
K
M
C1
A1
ВАЖНО!
Если секущая плоскость пересекает противоположные грани, то она пересекает их по
параллельным отрезкам.