- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Окружность и круг (5 класс)
Содержание
- 1. Презентация по математике на тему Окружность и круг (5 класс)
- 2. В русском языке слово
- 3. Без понятия круга и окружности
- 4. Самая простая из кривых линий
- 5. О1. Поставьте в тетради точку и обозначьте
- 6. ОТочка О называется центром окружностиО1. Поставьте в
- 7. Круг – часть плоскости, ограниченная окружностьюОкружность -
- 8. Слайд 8
- 9. Окружность.Окружностью называется геометрическая фигура, состоящая из всех
- 10. Откладывание отрезка, равного данному. Дано: отрезокПостроить: отрезок, равный данному.АОА=аа
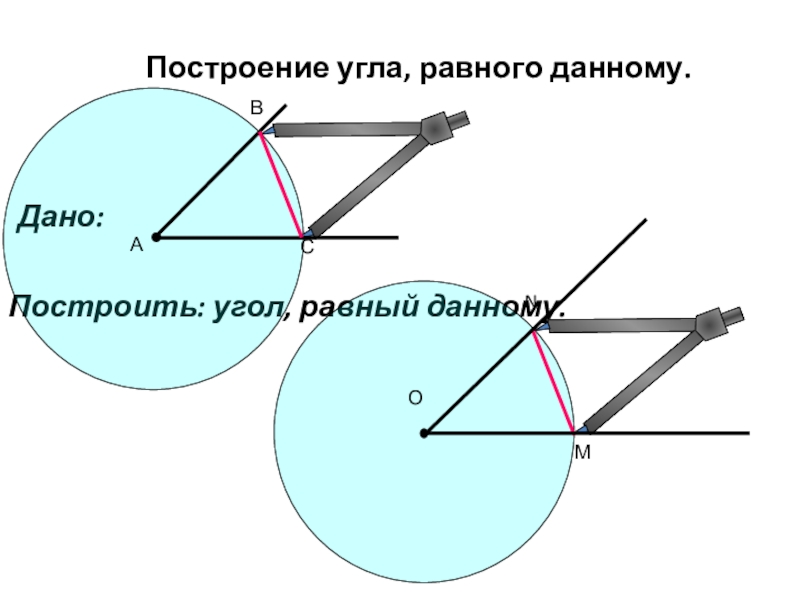
- 11. Построение угла, равного данному. Дано: Построить: угол, равный данному.ВСМN
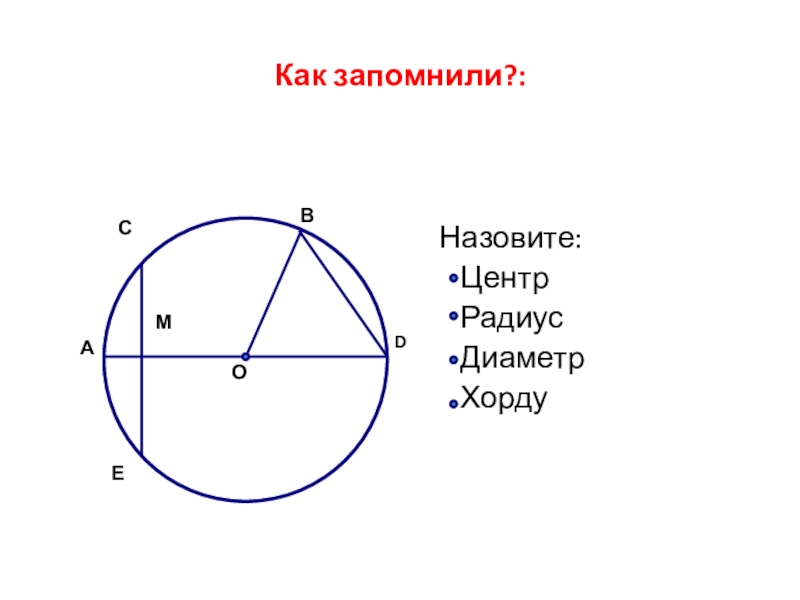
- 12. Как запомнили?:Назовите: Центр Радиус Диаметр ХордуЕОВDМАС
- 13. ТренажерНазовите точки, которые:Лежат на окружностиЛежат внутри кругаНе
- 14. Собери разбежавшиеся правила
- 15. Задание: Изучив таблицу, сформулируйте геометрические определения понятий, используя ключевые слова.
- 16. CАDВЗадание: Проведите прямые через каждые две точки.
- 17. AВПрактическая работа. Рассмотрите прямую m, точку М
Слайд 1Математика. 5 класс.
Тема «Окружность и круг»
ЗНАТЬ: ПОНЯТИЯ ОКРУЖНОСТИ, КРУГА, РАДИУСА, ДИАМЕТРА.
ФОРМИРОВАТЬ: УМЕНИЕ НАХОДИТЬ РАДИУС, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР, И ДИАМЕТР, ЕСЛИ ИЗВЕСТЕН РАДИУС.
Тип урока: урок получения новых знаний, умений и навыков.
Цели урока: обобщить и систематизировать знания по теме, ознакомление учащихся с понятием окружности и круга; формирование умения строить окружность с помощью циркуля по заданному радиусу и диаметру.
Учебные задачи, направленные на достижение:
Личностного развития:
продолжать развивать умение ясно, точно и грамотно излагать свои мысли в устной и письменной речи,
развивать креативность мышления, инициативу, находчивость, активность при решении математических задач.
Метапредметного развития:
расширять кругозор, прививать умение совместно работать (чувство товарищества и ответственности за результаты своего труда);
продолжать развивать умение понимать и использовать математические средства наглядности.
Предметного развития:
формировать теоретическое и практическое представление об окружности и круге, как о геометрических фигурах, их элементах;
продолжать развитие изобразительных умений (научить пользоваться циркулем для построения окружности любого радиуса);
формировать умение применять изученные понятия для решения задач практического характера.
Слайд 2
В русском языке слово «круглый» тоже означает
В школе свойства окружности и круга изучаются до 11 кл., но первые представления у учащихся должны быть уже в 5 кл.
Окружность – это геометрическая фигура, каждая точка которой равноудалена от одной точки – центра окружности.
Наглядным примером окружности является хулахуп (обруч).
Отрезок, соединяющий центр окружности с любой ее точкой, является радиусом окружности.
Диаметр окружности – это отрезок, соединяющий две точки окружности и проходящий через центр.
Круг – это часть плоскости, ограниченная окружностью. Блин, пожаренный на круглой сковороде, является кругом.
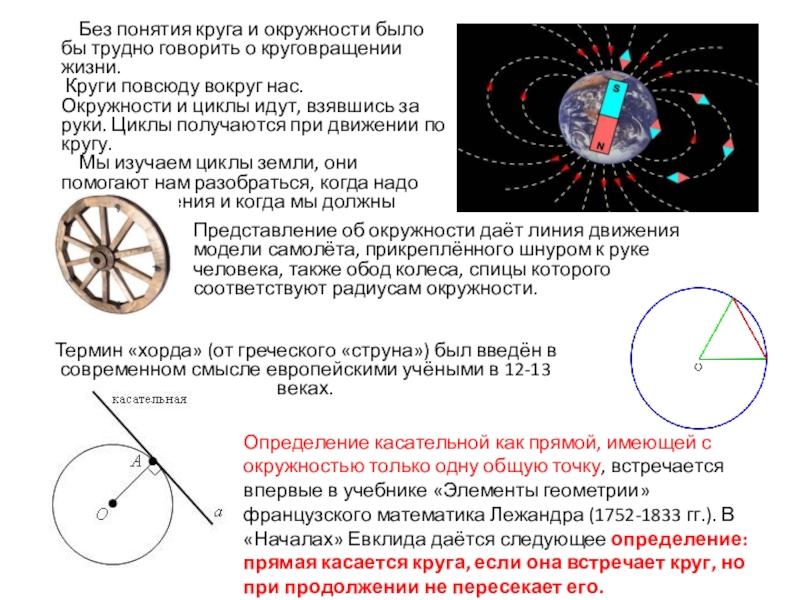
Слайд 3 Без понятия круга и окружности было бы трудно говорить
Круги повсюду вокруг нас. Окружности и циклы идут, взявшись за руки. Циклы получаются при движении по кругу.
Мы изучаем циклы земли, они помогают нам разобраться, когда надо сажать растения и когда мы должны вставать.
Представление об окружности даёт линия движения модели самолёта, прикреплённого шнуром к руке человека, также обод колеса, спицы которого соответствуют радиусам окружности.
Термин «хорда» (от греческого «струна») был введён в современном смысле европейскими учёными в 12-13 веках.
Определение касательной как прямой, имеющей с окружностью только одну общую точку, встречается впервые в учебнике «Элементы геометрии» французского математика Лежандра (1752-1833 гг.). В «Началах» Евклида даётся следующее определение: прямая касается круга, если она встречает круг, но при продолжении не пересекает его.
Слайд 4 Самая простая из кривых линий – окружность. Это
Ещё вавилоняне и древние индийцы считали самым важным элементом окружности – радиус. Слово это латинское и означает «луч».
В древности не было этого термина: Евклид и другие учёные говорили просто «прямая из центра», Ф. Виет писал что «радиус» - это «элегантное слово». Общепринятым термин «радиус» становится лишь в конце 17 в. Впервые термин «радиус» встречается в «Геометрии» французского ученого Пьер де ла Раме, изданной в 1569 году.
Евклид (3 век до нашей эры) – древнегреческий математик
Пьер де ла Раме (1515-1572) — французский философ, математик, педагог.
Франсуа Виет (1540-1603) –
французский математик
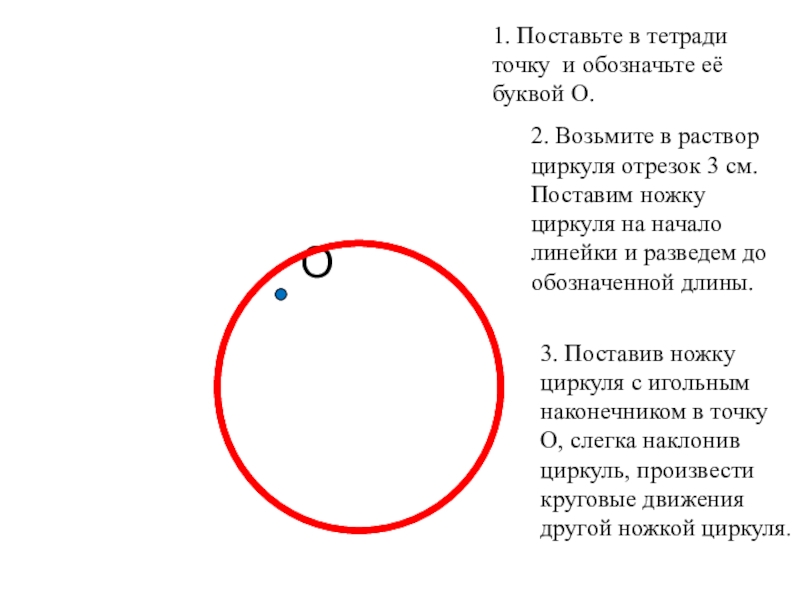
Слайд 5О
1. Поставьте в тетради точку и обозначьте её буквой О.
2. Возьмите
3. Поставив ножку циркуля с игольным наконечником в точку О, слегка наклонив циркуль, произвести круговые движения другой ножкой циркуля.
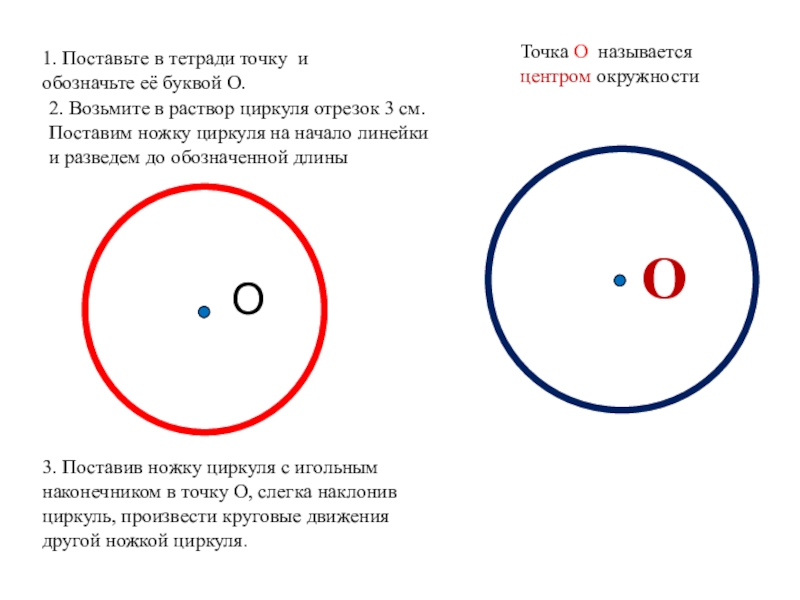
Слайд 6О
Точка О называется центром окружности
О
1. Поставьте в тетради точку и обозначьте
2. Возьмите в раствор циркуля отрезок 3 см. Поставим ножку циркуля на начало линейки и разведем до обозначенной длины
3. Поставив ножку циркуля с игольным наконечником в точку О, слегка наклонив циркуль, произвести круговые движения другой ножкой циркуля.
Слайд 7Круг – часть плоскости, ограниченная окружностью
Окружность - это замкнутая линия, все
Чем отличается окружность и круг друг от друга?
O
O
Построй две окружности и закрась внутреннюю область одной окружности.
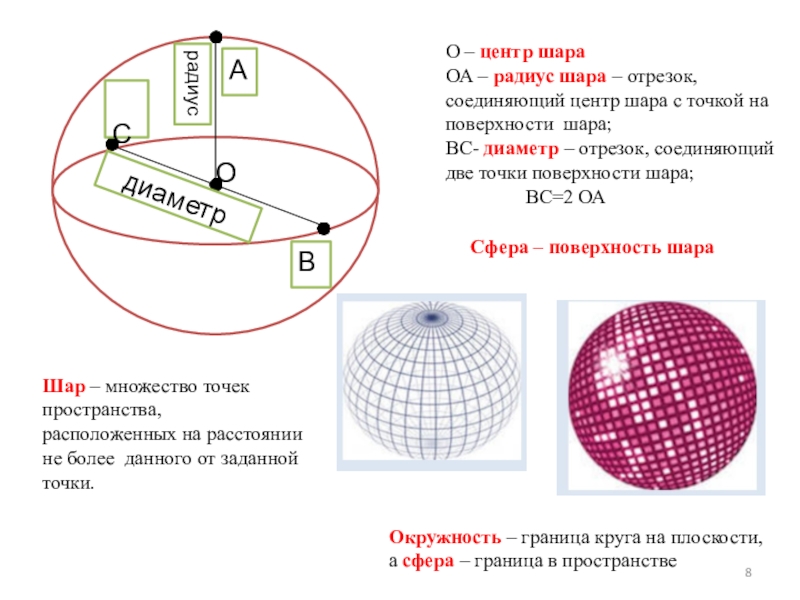
Слайд 8
А
диаметр
радиус
С
В
Шар – множество точек пространства,
расположенных на расстоянии не более данного от заданной точки.
О – центр шара
ОА – радиус шара – отрезок, соединяющий центр шара с точкой на поверхности шара;
ВС- диаметр – отрезок, соединяющий две точки поверхности шара;
ВС=2 ОА
Сфера – поверхность шара
Окружность – граница круга на плоскости,
а сфера – граница в пространстве
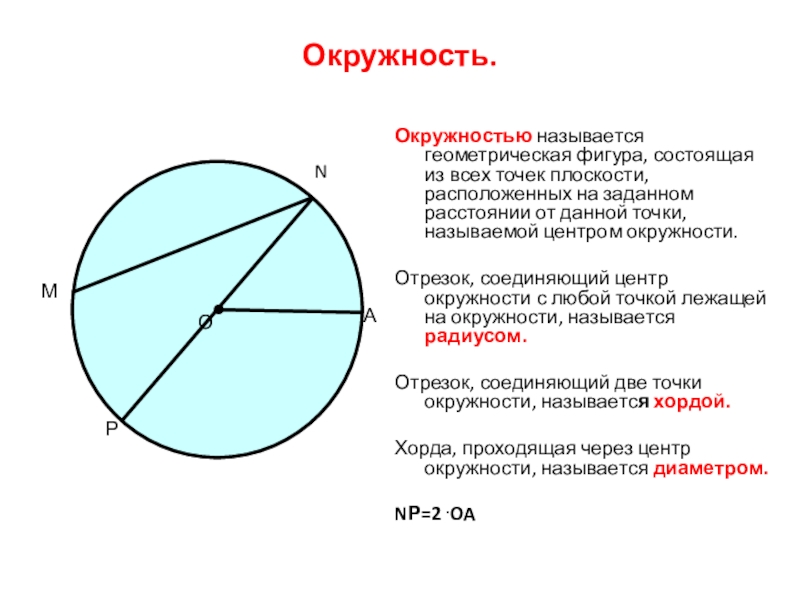
Слайд 9Окружность.
Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на
Отрезок, соединяющий центр окружности с любой точкой лежащей на окружности, называется радиусом.
Отрезок, соединяющий две точки окружности, называется хордой.
Хорда, проходящая через центр окружности, называется диаметром.
NР=2 .OA
М
N
А
Р
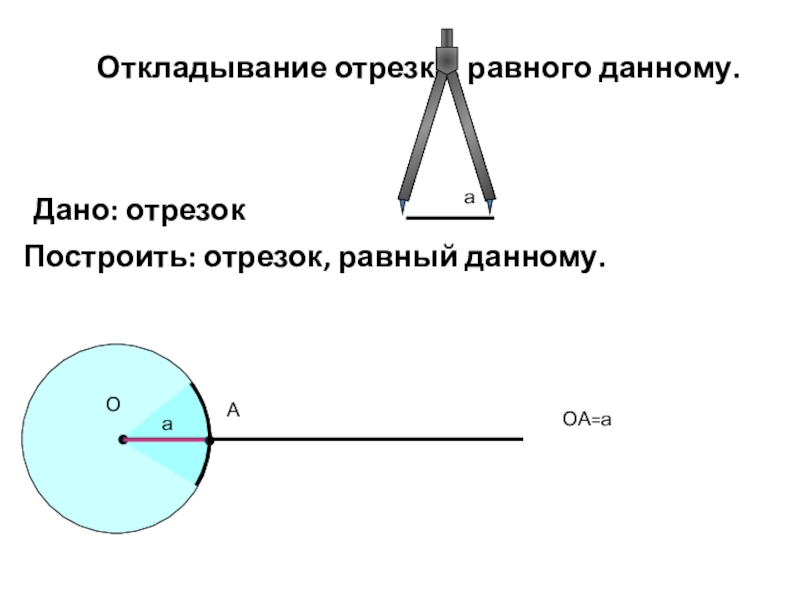
Слайд 10Откладывание отрезка, равного данному.
Дано: отрезок
Построить: отрезок, равный данному.
А
ОА=а
а
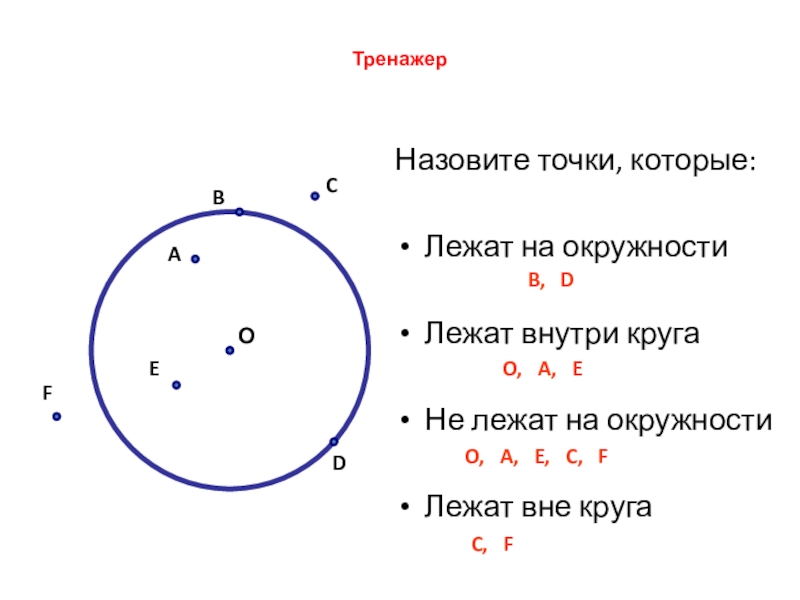
Слайд 13Тренажер
Назовите точки, которые:
Лежат на окружности
Лежат внутри круга
Не лежат на окружности
Лежат вне
О
E
A
B
C
D
F
B, D
O, A, E
O, A, E, C, F
C, F
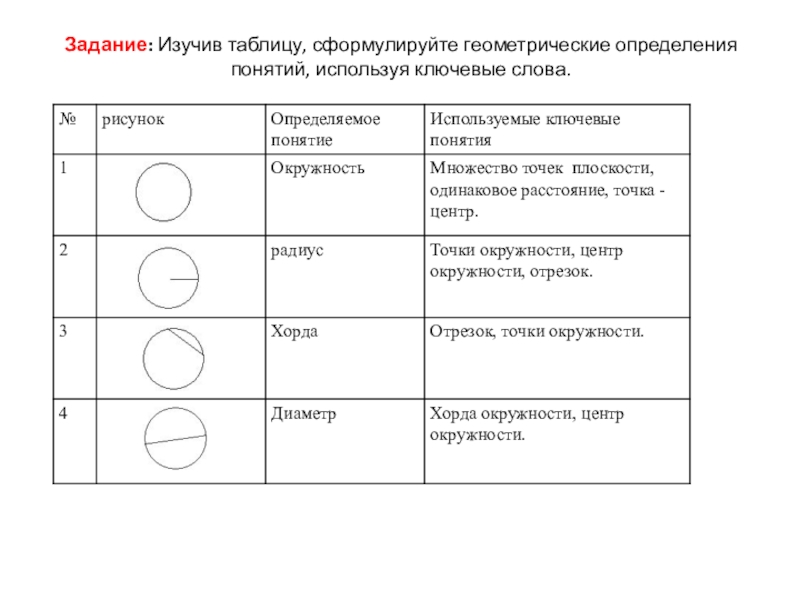
Слайд 15Задание: Изучив таблицу, сформулируйте геометрические определения понятий, используя ключевые слова.
Слайд 16C
А
D
В
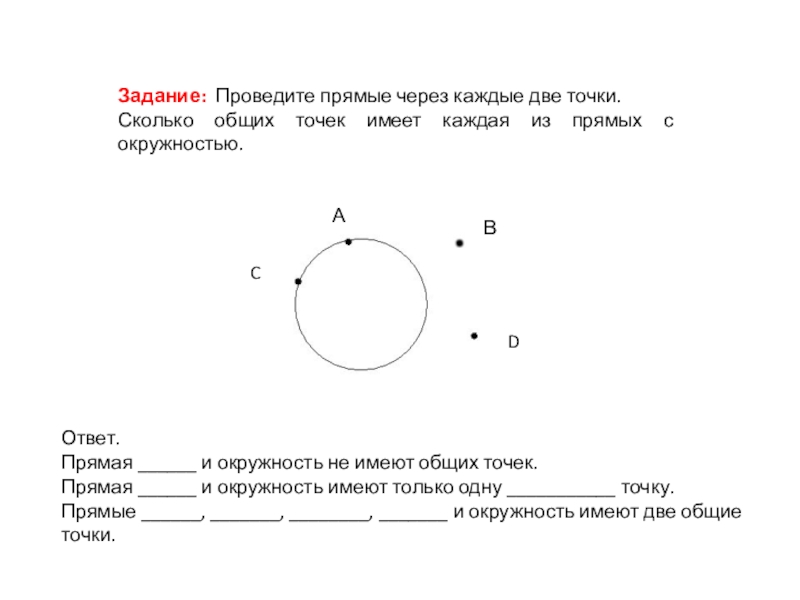
Задание: Проведите прямые через каждые две точки.
Сколько общих точек имеет
Ответ.
Прямая ______ и окружность не имеют общих точек.
Прямая ______ и окружность имеют только одну ___________ точку.
Прямые ______, _______, ________, _______ и окружность имеют две общие точки.
Слайд 17A
В
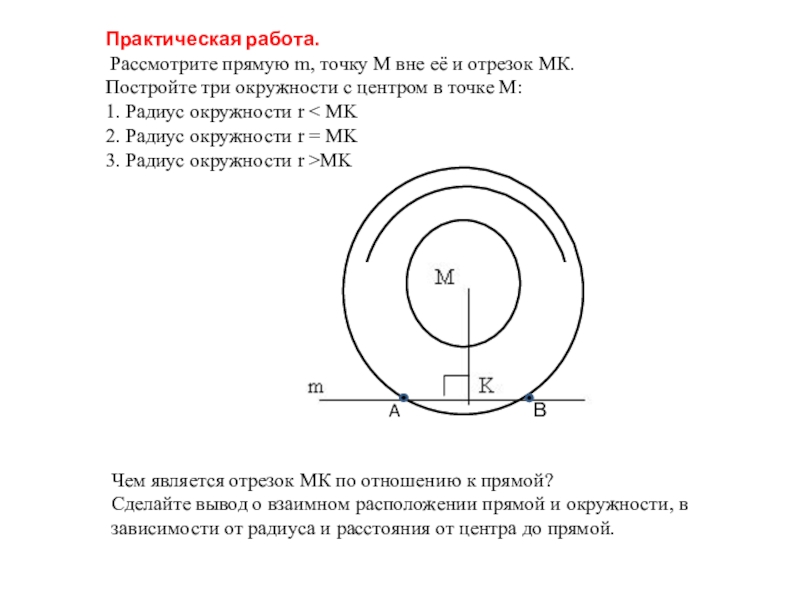
Практическая работа.
Рассмотрите прямую m, точку М вне её и отрезок
Постройте три окружности с центром в точке М:
1. Радиус окружности r < MK
2. Радиус окружности r = MK
3. Радиус окружности r >MK
Чем является отрезок МК по отношению к прямой?
Сделайте вывод о взаимном расположении прямой и окружности, в зависимости от радиуса и расстояния от центра до прямой.