Воробьева Екатерина Сергеевна, 6 класс
Ефимович Мария Сергеевна, 6 класс
МБОУ СШ №72
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему О паркетных гранях выпуклых правильногранников (6 класс)
Содержание
- 1. Презентация по математике на тему О паркетных гранях выпуклых правильногранников (6 класс)
- 2. Цель Получить практическим путем паркетные многоугольники, составленные
- 3. Задачи:- Какие паркетные многоугольники со сторонами длины
- 4. Евклид и АрхимедЕвклид – древнегреческий учёный. Он
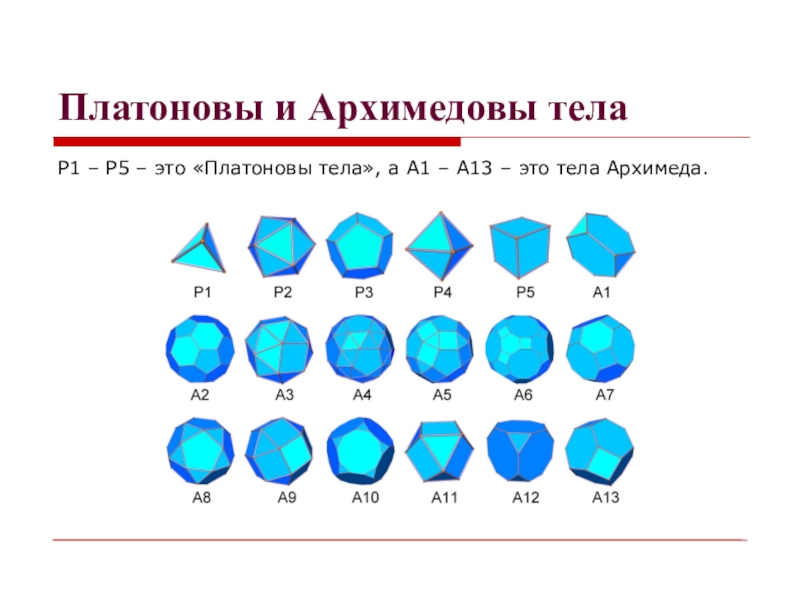
- 5. Платоновы и Архимедовы телаP1 – P5 –
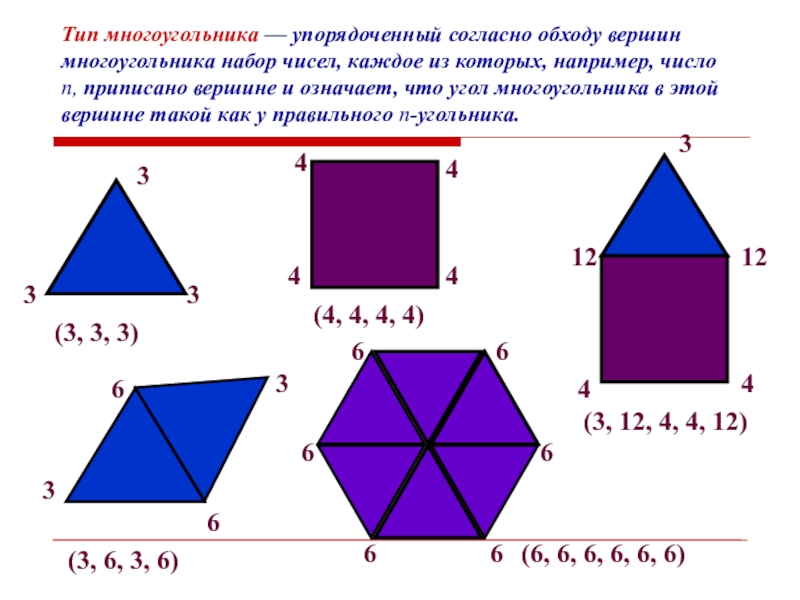
- 6. 3(3, 6, 3, 6)6666(6, 6, 6, 6,
- 7. М21М33Моделирование многоугольников из правильных треугольников и квадратов с единичными ребрами (типы многоугольников)
- 8. Слайд 8
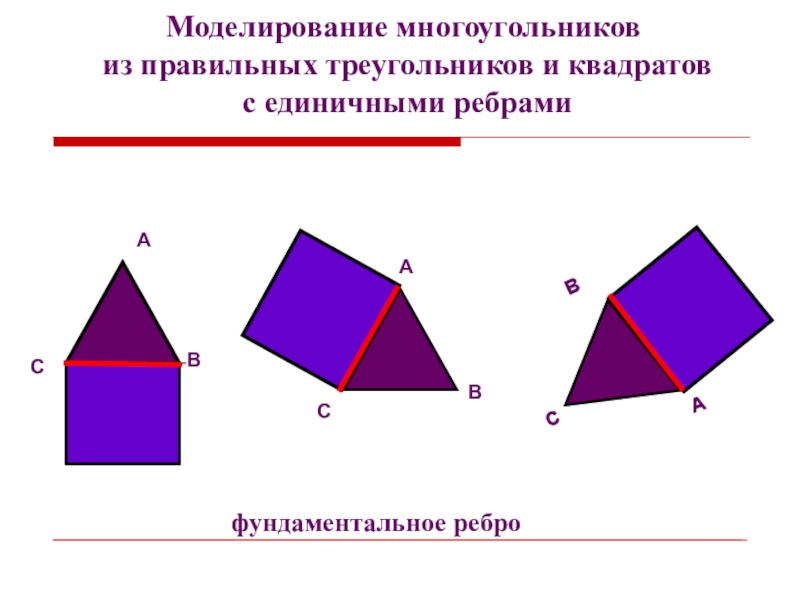
- 9. Моделирование многоугольников из правильных треугольников и квадратов с единичными ребрамифундаментальное ребро
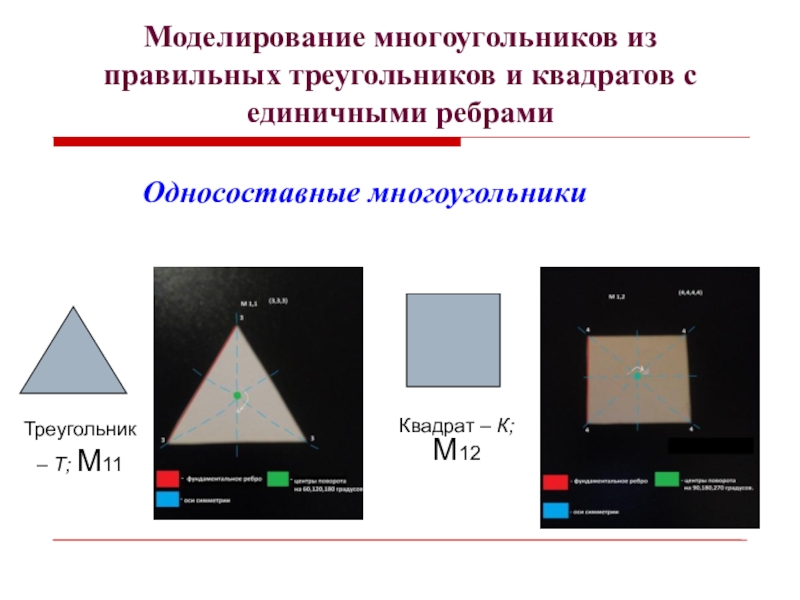
- 10. Моделирование многоугольников из правильных треугольников и квадратов
- 11. Моделирование многоугольников из правильных треугольников и квадратов с единичными ребрамиДвусоставные многоугольникиМ
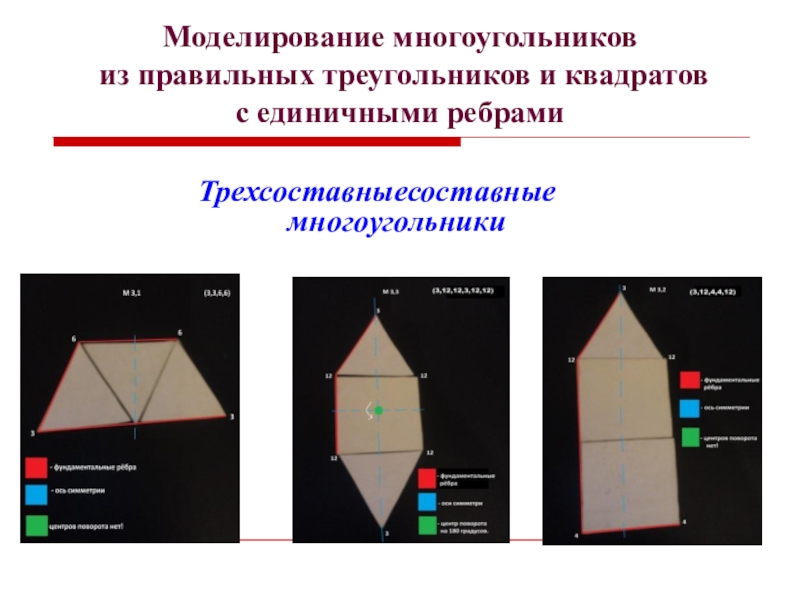
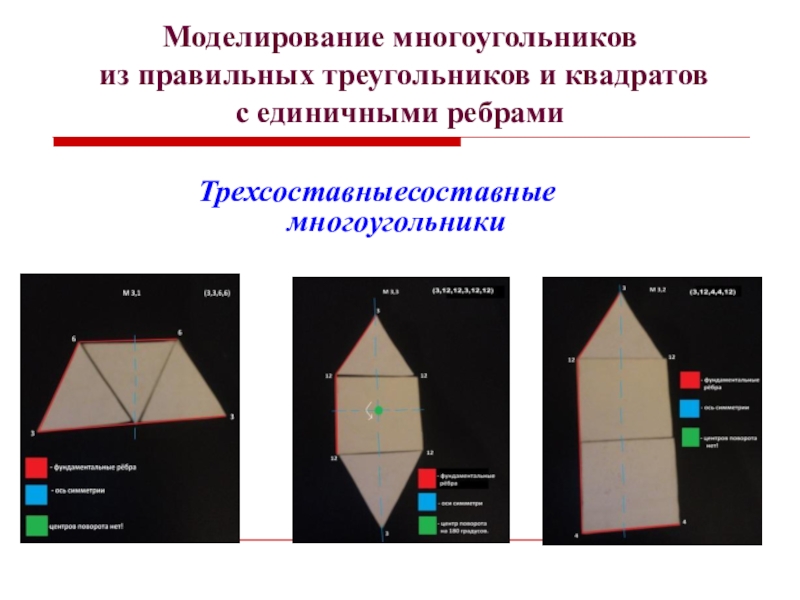
- 12. Моделирование многоугольников из правильных треугольников и квадратов с единичными ребрамиТрехсоставныесоставные многоугольники
- 13. Моделирование многоугольников из правильных треугольников и квадратов с единичными ребрамиТрехсоставныесоставные многоугольники
- 14. Моделирование многоугольников из правильных треугольников и квадратов с единичными ребрамиЧетырехсоставные многоугольники
- 15. Моделирование многоугольников из правильных треугольников и квадратов с единичными ребрамиПятисоставные многоугольники
- 16. Моделирование многоугольников из правильных треугольников и квадратов с единичными ребрамиШестисоставные многоугольники
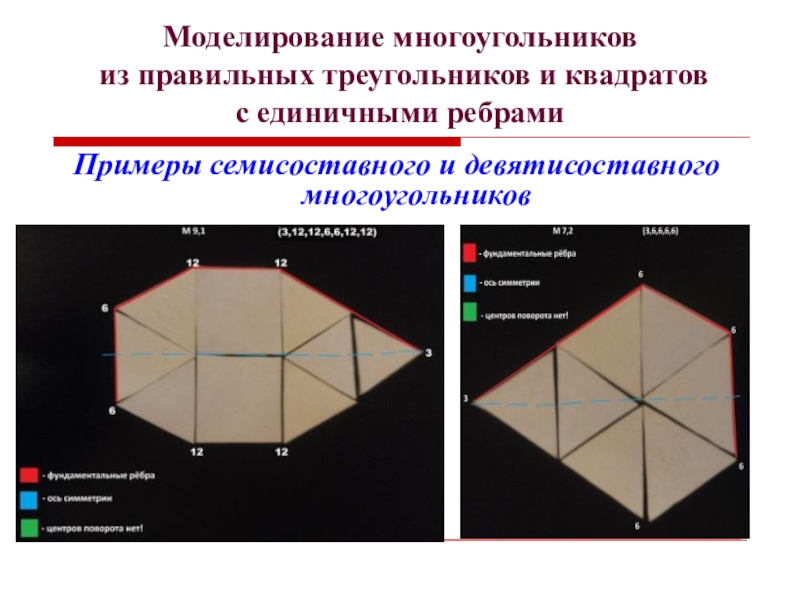
- 17. Моделирование многоугольников из правильных треугольников и квадратов с единичными ребрамиПримеры семисоставного и девятисоставного многоугольников
- 18. Моделирование многоугольников из правильных треугольников и квадратов с единичными ребрамиВосьмисоставные многоугольники
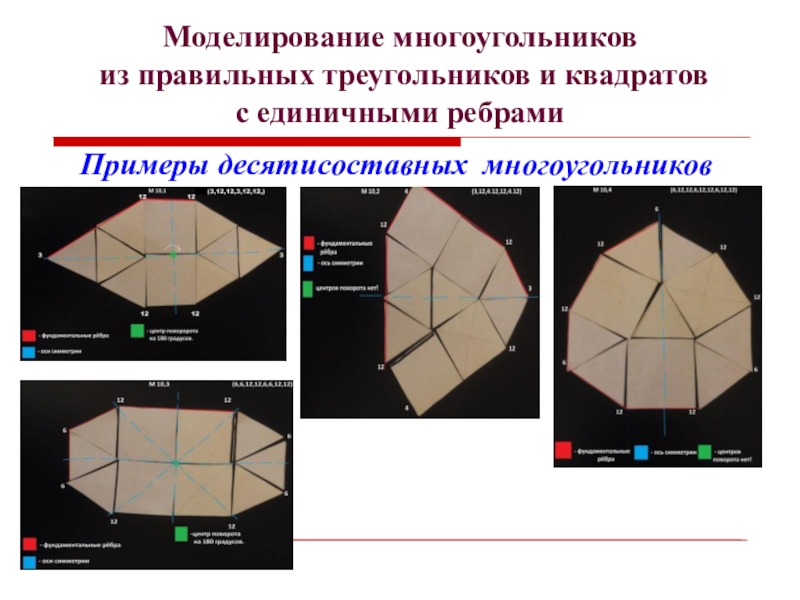
- 19. Моделирование многоугольников из правильных треугольников и квадратов с единичными ребрамиПримеры десятисоставных многоугольников
- 20. Публикация моделей паркетных многоугольников в издании КГПУ
- 21. Вывод: Существует ровно 16 выпуклых
Цель Получить практическим путем паркетные многоугольники, составленные из правильных треугольников и квадратов с единичными ребрами, так, что стороны самого паркетного многоугольника имеют длины, не превосходящие два. Внести свой вклад в решение фундаментальной научной проблемы: «Каковы
Слайд 1КАКОВЫ ВСЕ ВЫПУКЛЫЕ МНОГОУГОЛЬНИКИ, СОСТАВЛЕННЫЕ ИЗ ПРАВИЛЬНЫХ ТРЕУГОЛЬНИКОВ И КВАДРАТОВ С
ЕДИНИЧНЫМИ РЕБРАМИ
Слайд 2Цель
Получить практическим путем паркетные многоугольники, составленные из правильных треугольников и
квадратов с единичными ребрами, так, что стороны самого паркетного многоугольника имеют длины, не превосходящие два.
Внести свой вклад в решение фундаментальной научной проблемы:
«Каковы все выпуклые многогранники, каждая грань которых, составлена из одного или нескольких правильных многоугольников?»
Внести свой вклад в решение фундаментальной научной проблемы:
«Каковы все выпуклые многогранники, каждая грань которых, составлена из одного или нескольких правильных многоугольников?»
Слайд 3Задачи:
- Какие паркетные многоугольники со сторонами длины один или два, можно
получить путём соединения по рёбрам правильных многоугольников с единичными сторонами:
1) треугольников;
2) квадратов;
3) треугольников и квадратов?
- Найти способ соединения многоугольников;
- Составить таблицу соединений.
1) треугольников;
2) квадратов;
3) треугольников и квадратов?
- Найти способ соединения многоугольников;
- Составить таблицу соединений.
Слайд 4Евклид и Архимед
Евклид – древнегреческий учёный. Он прославился тем, что написал
«Начала», в которых из постулатов и аксиом вывел теоремы. Логически «Начала» ведут к построению пяти правильных тел: тетраэдра, икосаэдра, октаэдра, куба и додекаэдра.
Архиме́д –древнегреческий учёный и изобретатель. Сделал множество открытий в области геометрии. Он открыл 13 равноугольно-полуправильных тел, называемых сегодня архимедовыми.
Слайд 63
(3, 6, 3, 6)
6
6
6
6
(6, 6, 6, 6, 6, 6)
Тип многоугольника —
упорядоченный согласно обходу вершин многоугольника набор чисел, каждое из которых, например, число n, приписано вершине и означает, что угол многоугольника в этой вершине такой как у правильного n-угольника.
Слайд 7М21
М33
Моделирование многоугольников
из правильных треугольников и квадратов
с единичными ребрами (типы
многоугольников)
Слайд 9Моделирование многоугольников
из правильных треугольников и квадратов
с единичными ребрами
фундаментальное ребро
Слайд 10Моделирование многоугольников из правильных треугольников и квадратов с единичными ребрами
Треугольник –
Т; М11
Квадрат – К; М12
Односоставные многоугольники
Слайд 11Моделирование многоугольников
из правильных треугольников и квадратов
с единичными ребрами
Двусоставные многоугольники
М
Слайд 12Моделирование многоугольников
из правильных треугольников и квадратов
с единичными ребрами
Трехсоставныесоставные многоугольники
Слайд 13Моделирование многоугольников
из правильных треугольников и квадратов
с единичными ребрами
Трехсоставныесоставные многоугольники
Слайд 14Моделирование многоугольников
из правильных треугольников и квадратов
с единичными ребрами
Четырехсоставные многоугольники
Слайд 15Моделирование многоугольников
из правильных треугольников и квадратов
с единичными ребрами
Пятисоставные многоугольники
Слайд 16Моделирование многоугольников
из правильных треугольников и квадратов
с единичными ребрами
Шестисоставные многоугольники
Слайд 17Моделирование многоугольников
из правильных треугольников и квадратов
с единичными ребрами
Примеры семисоставного
и девятисоставного многоугольников
Слайд 18Моделирование многоугольников
из правильных треугольников и квадратов
с единичными ребрами
Восьмисоставные многоугольники
Слайд 19Моделирование многоугольников
из правильных треугольников и квадратов
с единичными ребрами
Примеры десятисоставных
многоугольников
Слайд 20Публикация моделей паркетных многоугольников
в издании КГПУ им. Астафьева «ВЕСТНИК»
статья
А.В.
Тимофеенко,
Е.С. Отмаховой «Комплекс решений, необходимых для организации работы над научной проблемой коллективом сотрудников и студентов»
Е.С. Отмаховой «Комплекс решений, необходимых для организации работы над научной проблемой коллективом сотрудников и студентов»
Слайд 21Вывод:
Существует ровно 16 выпуклых соединений, составленных не более,
чем из шести правильных треугольников и квадратов с единичными рёбрами, причём длины рёбер каждого соединения не больше, чем два.
Каждое из этих соединений найдено в явном виде.
Каждое из этих соединений найдено в явном виде.