- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Методика обучения решения текстовых задач
Содержание
- 1. Презентация по математике на тему Методика обучения решения текстовых задач
- 2. 5 класс Здесь осуществляется подготовительный этап – учимся составлять математические модели:числовые выражения;буквенные выражения;уравнения.
- 3. Числовые выраженияБуквенные выраженияx = 18, y
- 4. В систему заданий последующих параграфов учебника включены
- 5. §16. МАТЕМАТИЧЕСКИЙ ЯЗЫК Целиком посвящен этому понятию:математический
- 6. §17. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ Здесь вводится понятие математической
- 7. 300 : (180 : 2 + 180
- 8. ДанныеМатематическая модельВ стаде а овец и b
- 9. ?231. В одной коробке носки голубые, а
- 10. Метод уравнивания20 п.Б.Г.84 п.?231. В одной коробке
- 11. ?232. В магазине имеется крупа трех видов:
- 12. Г.П.Р.580 кг
- 13. ?240. В булочную завезли хлеб трех сортов,
- 14. № 240.IIIIII30 б.30 б.30 б.30 б.151515Решение:1) 30
- 15. 241. На земельном участке площадью 204 а
- 16. № 241к а р т о ф е л ь204 а
- 17. В § 27 включено учебное задание №509,
- 18. ?519. 1) Масса трех кусков мрамора –
- 19. 32 кг14 кгРешение:1) 280 – (32 +14)
- 20. 2) x кг – масса второго куска
- 21. У544. 1) Решите задачу.На первом элеваторе зерна
- 22. У 544.850 т150 т700 т350 т350 т350 тIII
- 23. У 544.850 т150 т700 т350 т350 т350
- 24. У551. 1) Прочитайте задачу.В магазине было два
- 25. У 551.Математическая модель в виде схемы (графическая):17 м17 м17 м
- 26. У 551.Математическая модель в виде схемы (графическая):Математическая
- 27. x + 45 = 2x + 28Полученное
- 28. 637. В двух кусках поровну ткани. После
- 29. №637.14 м8 м4 м4 м4 м4 м
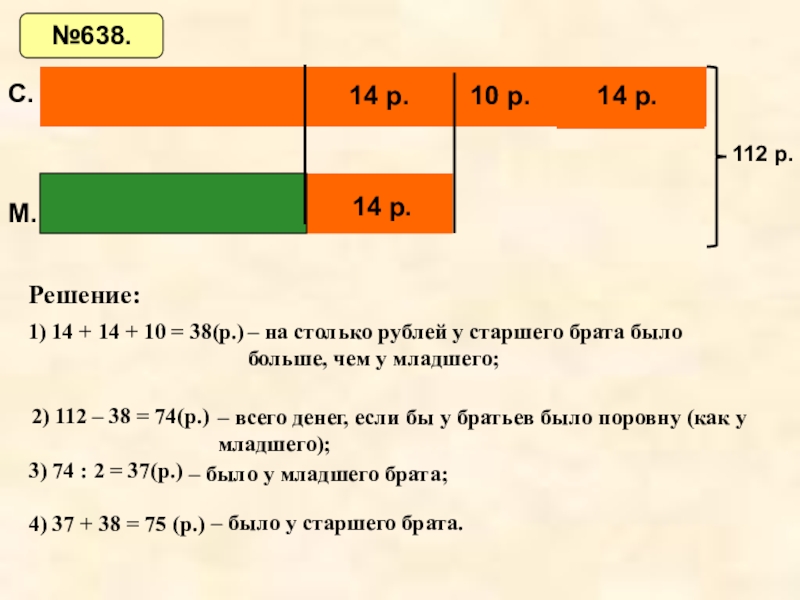
- 30. 638. У двоих братьев было вместе 112
- 31. 14 р.14 р.10 р.14 р.112 р.№638.С.М.
- 32. 6 класс продолжается работа по формированию умений
- 33. Устные упражнения1) – 5x = 102) 2x
- 34. В одном бидоне х л, а в другом
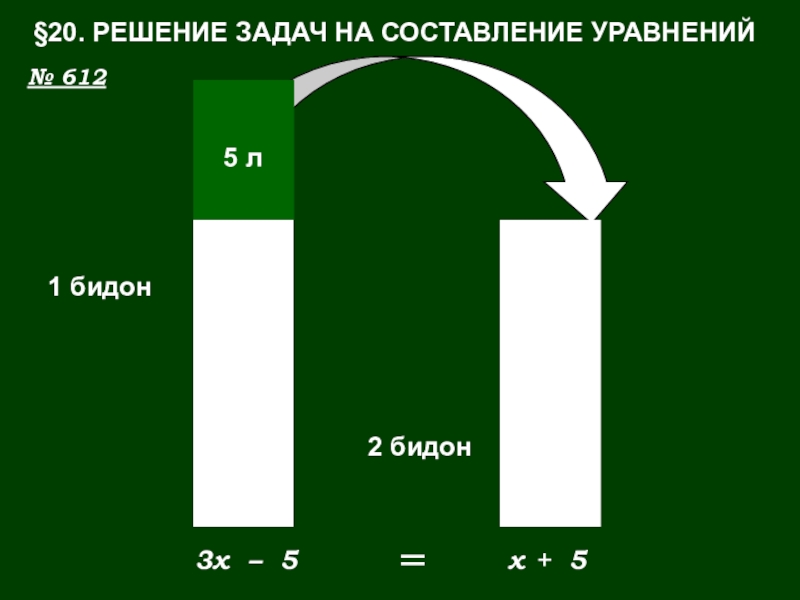
- 35. 1 бидон2 бидонx3x– 5+ 5=§20. РЕШЕНИЕ ЗАДАЧ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ№ 612
- 36. Пусть x л – количество молока во
- 37. III. Ответ на вопрос задачи5 л –
- 38. 1 автостоянка2 автостоянка
- 39. 1 автостоянка2 автостоянкаБылоСталоx м(4x – 12) м(x
- 40. Спасибо за внимание!
Слайд 25 класс
Здесь осуществляется подготовительный этап –
учимся составлять математические модели:
числовые
буквенные выражения;
уравнения.
Слайд 3Числовые выражения
Буквенные выражения
x = 18, y = 6
x р. за
y р. за 1 кг
15 р.
5 р.
§2. Числовые и буквенные выражения
Слайд 4В систему заданий последующих параграфов учебника включены задания следующих типов:
1) составить
2) составить равенство, содержащее буквенные выражения, в соответствии с заданной ситуацией;
3) расшифровать смысл данного выражения в соответствии с заданной ситуацией;
4) расшифровать смысл данного равенства в соответствии с заданной ситуацией.
Уже в §2 вводится термин «математический язык».
Слайд 5§16. МАТЕМАТИЧЕСКИЙ ЯЗЫК
Целиком посвящен этому понятию:
математический алфавит;
числовые и буквенные выражения
слова, связанные знаками =, >, <, ≠, ≈, – это предложения, записанные на математическом языке.
В этом параграфе учащиеся наряду с равенствами составляют и расшифровывают неравенства.
Слайд 6§17. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Здесь вводится понятие математической модели.
Внимание учащихся акцентируется на
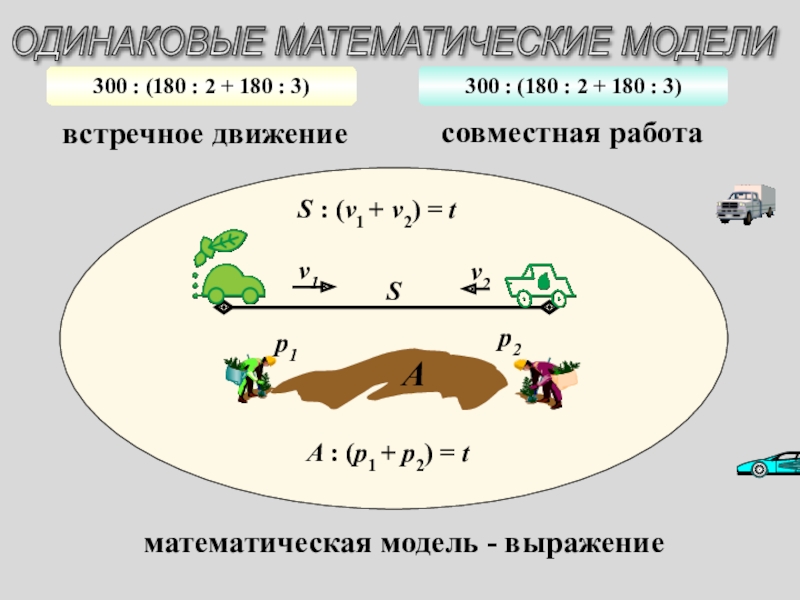
Слайд 7300 : (180 : 2 + 180 : 3)
300 : (180
ОДИНАКОВЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
v1
v2
S
S : (v1 + v2) = t
A : (p1 + p2) = t
встречное движение
совместная работа
математическая модель - выражение
Слайд 8Данные
Математическая
модель
В стаде а овец и b коров.
Турист а км прошел
За конфеты заплатили а р., а за печенье b р.
В классе а девочек и b мальчиков.
a + b = 30
математическая модель - равенство
Слайд 9?231. В одной коробке носки голубые, а в другой - белые.
Параллельно с этим в систему заданий включаются
задачи на уравнивание.
Слайд 10Метод уравнивания
20 п.
Б.
Г.
84 п.
?231. В одной коробке носки голубые, а в
Слайд 11?232. В магазине имеется крупа трех видов: гречка, перловка и рис,
Слайд 13?240. В булочную завезли хлеб трех сортов, одинаковое количество батонов каждого
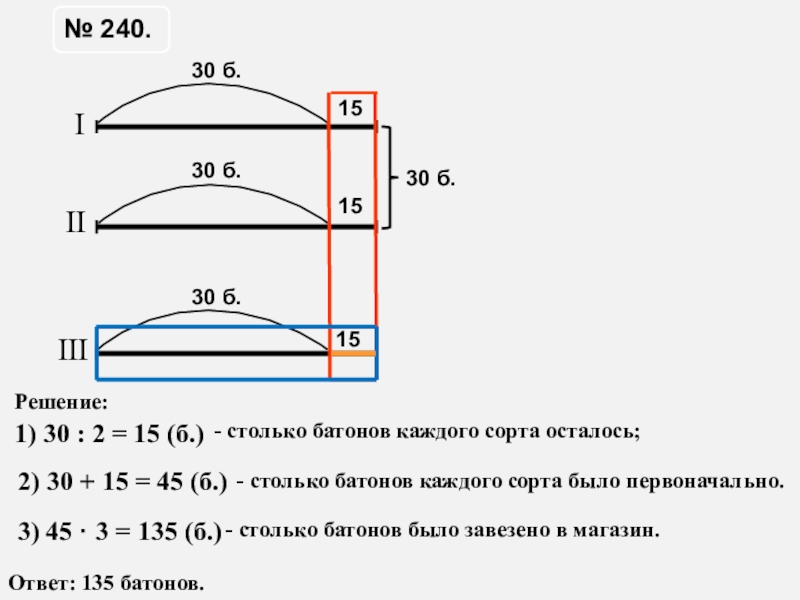
Слайд 14№ 240.
I
II
III
30 б.
30 б.
30 б.
30 б.
15
15
15
Решение:
1) 30 : 2 = 15
- столько батонов каждого сорта осталось;
2) 30 + 15 = 45 (б.)
- столько батонов каждого сорта было первоначально.
3) 45 · 3 = 135 (б.)
- столько батонов было завезено в магазин.
Ответ: 135 батонов.
Слайд 15241. На земельном участке площадью 204 а выращивают картофель и капусту,
Слайд 17В § 27 включено учебное задание №509, в котором предлагается найти
В двух коробках 16 кг печенья. Найдите массу печенья в каждой коробке, если в одной из них печенья на 4 кг больше, чем в другой.
Рассматриваются способы решения этой задачи методом уравнивания и с помощью уравнения.
После этого вводятся понятия:
«арифметический способ»,
«алгебраический способ».
Слайд 18?519. 1) Масса трех кусков мрамора – 280 кг. Первый кусок
2) Обозначьте массу второго куска мрамора буквой х и составьте выражения для следующих величин:
масса первого куска мрамора;
масса третьего куска мрамора;
масса трех кусков мрамора.
3) Значение какого из полученных выражений указано в условии задачи? Ответ запишите в виде уравнения.
4) Решите полученное уравнение.
Слайд 19
32 кг
14 кг
Решение:
1) 280 – (32 +14) = 234 (кг)
–
280 кг
2) 234 : 3 = 78 (кг)
- масса 2-го куска.
3) 78 +32 = 110 (кг)
- масса 1-го куска.
4) 78 +14 = 92 (кг)
- масса 3-го куска.
Ответ: 110 кг, 78 кг, 92 кг.
Метод уравнивания + алгебраический метод
№ 519.
Слайд 202) x кг – масса второго куска мрамора.
(x + 14) кг
(x + 32) кг – масса первого куска мрамора;
(x + 32 + x + x + 14) кг – масса трех кусков мрамора.
3) x + 32 + x + x + 14 = 280
4) 3x + 46 = 280;
3x = 280 – 46;
3x = 234;
x = 234 : 3;
x = 78.
Метод уравнивания + алгебраический метод
№ 519.
78 +32 = 110 (кг) - масса первого куска;
78 +14 = 92 (кг) - масса третьего куска.
Ответ: 110 кг, 78 кг, 92 кг.
3) Значение какого из полученных выражений указано в условии задачи? Ответ запишите в виде уравнения.
4) Решите полученное уравнение.
Слайд 21У544. 1) Решите задачу.
На первом элеваторе зерна в три раза больше,
Если вы догадались составить к задаче такую схему, то, возможно, вы смогли решить ее устно (рис.103):
Постепенно уровень сложности задач повышается.
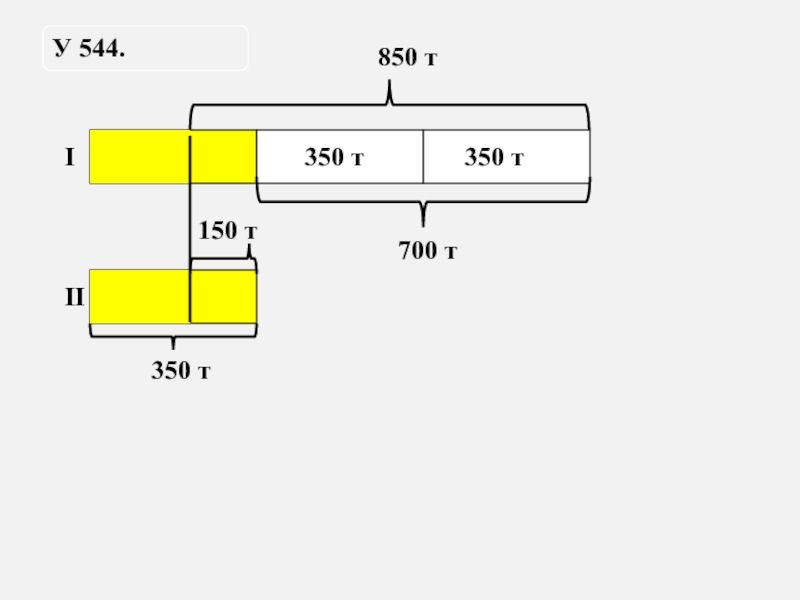
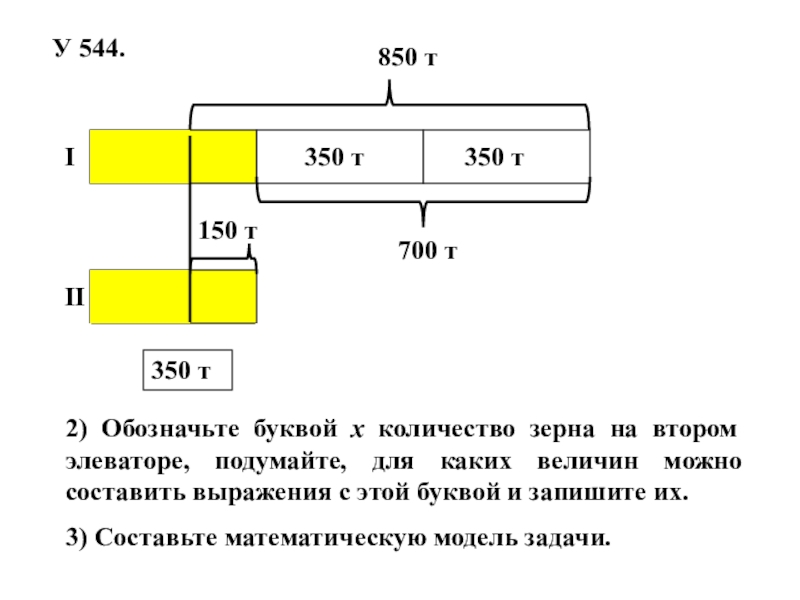
Слайд 23У 544.
850 т
150 т
700 т
350 т
350 т
350 т
I
II
2) Обозначьте буквой х
3) Составьте математическую модель задачи.
Слайд 24
У551. 1) Прочитайте задачу.
В магазине было два куска сатина одинаковой длины:
2) Составьте к этой задаче математическую модель в виде схемы, аналогичной той, которая была составлена к задаче про элеваторы с зерном (№544), и решите её устно.
Слайд 26
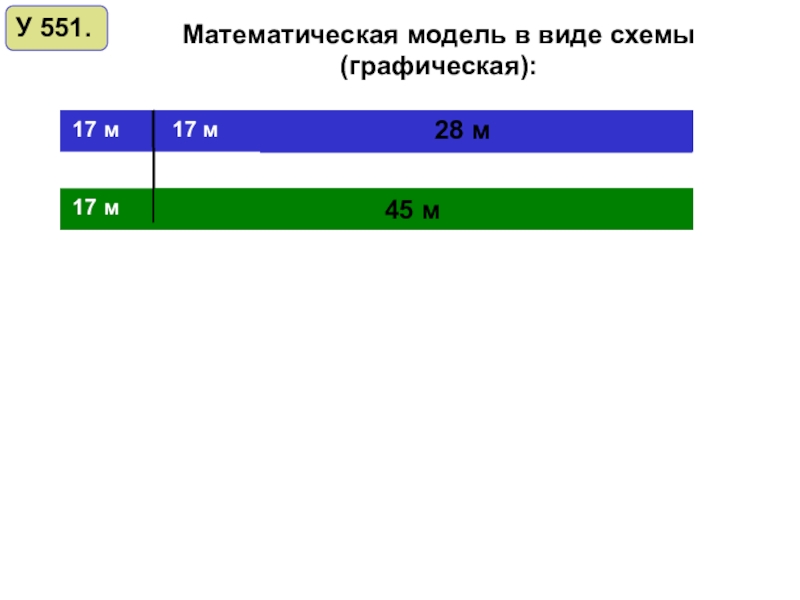
У 551.
Математическая модель в виде схемы (графическая):
Математическая модель в виде уравнения
(x + 45) м – было зелёной ткани первоначально;
2x м – осталось синей ткани;
x + 45 = 2x + 28
(2x + 28) м – было синей ткани первоначально.
x м – осталось зеленой ткани;
17 м
17 м
17 м
х
х
х
3) Составьте математическую модель задачи, последовательно выполнив следующие задания:
а) Обозначьте буквой х количество ткани, оставшейся во втором куске, подумайте, для каких величин можно составить выражения с этой буквой и запишите эти выражения.
б) Какие из составленных вами выражений соответствуют равным величинам? Ответ запишите в виде уравнения.
Слайд 27x + 45 = 2x + 28
Полученное уравнение дети на данном
Основная цель такой работы в 5 классе –
научить составлять уравнения.
Учитель ставит цель на будущее – в дальнейшем научиться решать и такие уравнения.
Слайд 28637. В двух кусках поровну ткани. После того как от первого
Слайд 30638. У двоих братьев было вместе 112 р. После того как
Слайд 326 класс
продолжается работа по формированию умений составления математических моделей;
знакомство с
решение уравнений методом переноса слагаемых из одной части равенства в другую;
решение задач выделением трёх этапов математического моделирования.
Слайд 34В одном бидоне х л, а в другом - у л молока.
1.
а) х + у
б) x + 3
в) y – 2
г) x - y
2. Расшифруйте равенства:
а) х + у = 90
б) x + 5 = y
в) 3x = y
г) x – 15 = y + 25
Слайд 36Пусть x л – количество молока во 2-ом бидоне до переливания.
3x
(3x – 5) л – осталось в 1-ом бидоне;
(x + 5) л – стало во 2-ом бидоне.
Зная, что после переливания молока в обоих бидонах стало поровну, составим уравнение:
I. Составление математической модели (составление уравнения)
3x – 5 =
x + 5.
3x– x = 5 + 5,
2x = 10,
x = 10 : 2,
x = 5.
II. Работа над математической моделью (решение уравнения)
СММ
Тогда:
РММ
Слайд 37III. Ответ на вопрос задачи
5 л – столько молока во 2-ом
5 · 3 = 15 (л) – столько молока в 1-ом бидоне
Ответ: 15 л, 5 л.
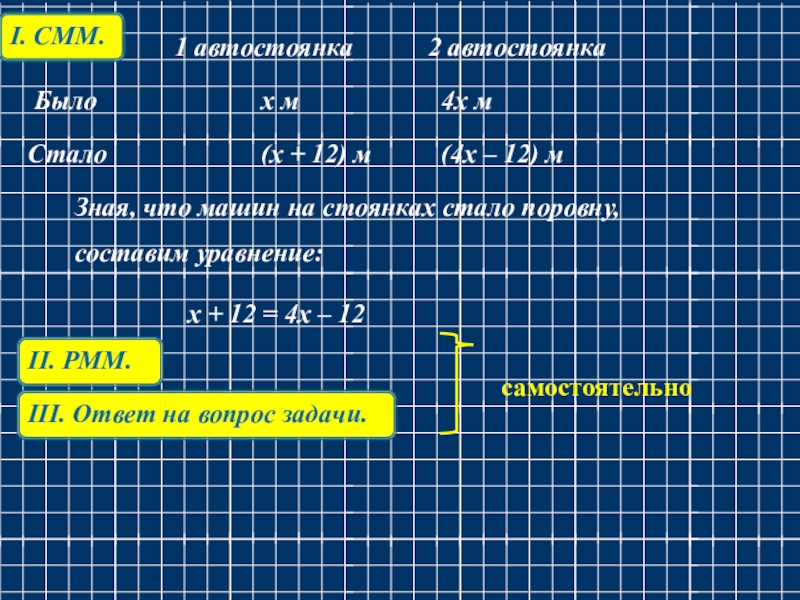
Слайд 391 автостоянка
2 автостоянка
Было
Стало
x м
(4x – 12) м
(x + 12) м
4x м
Зная,
составим уравнение:
x + 12 = 4x – 12
I. СММ.
II. РММ.
III. Ответ на вопрос задачи.
самостоятельно