- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Маленькие секреты клетчатой бумаги
Содержание
- 1. Презентация по математике на тему Маленькие секреты клетчатой бумаги
- 2. «... Только то обучение является хорошим, которое
- 3. научиться вычислять площади многоугольников с вершинами в
- 4. Задачи:Изучить литературу по данной теме;2. Рассмотреть
- 5. Слайд 5
- 6. Я пишу на бумаге в клетку.Не люблю
- 7. Игры на листе в клетку
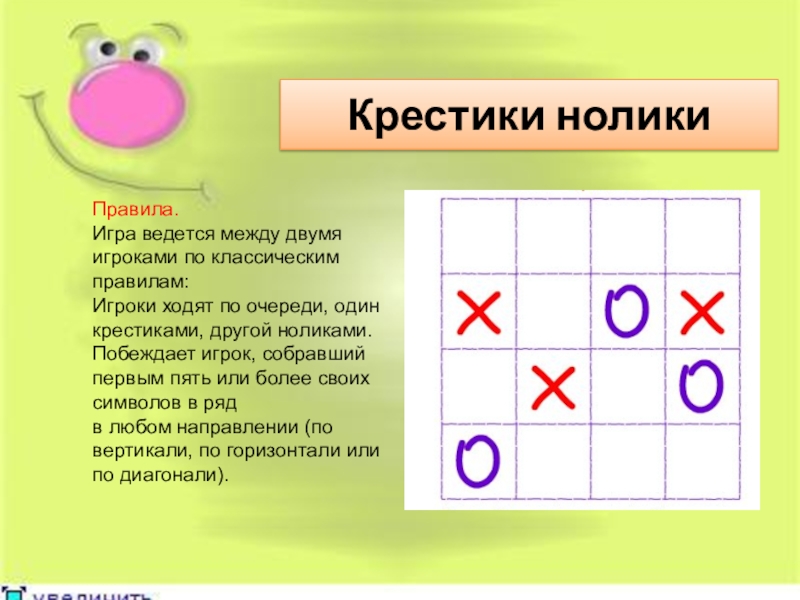
- 8. Крестики нолики Правила.Игра ведется между двумя
- 9. Морской бой Каждый игрок расставляет на
- 10. Логическая игра на бумаге "Тупик". Цель этой
- 11. Классические судоку 3х3 Необходимо заполнить свободные клетки
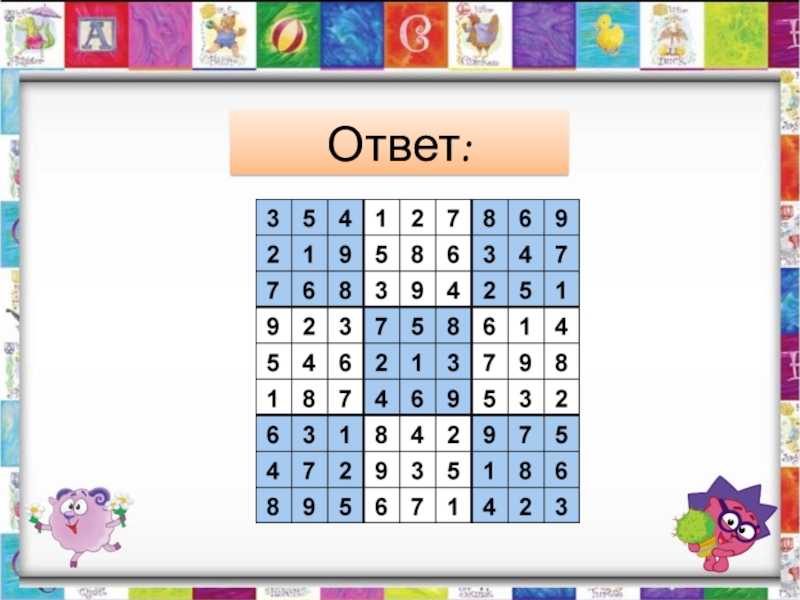
- 12. Ответ:
- 13. Судоку чёт-нечетВ этих судоку содержится дополнительная информация
- 14. Ответ:
- 15. Площади
- 16. Основание Карфагена Об основании древнего города Карфагена существует
- 17. Попробуем вычислить, какую площадь могла, согласно
- 18. Вычисление площадей с помощью формулы Пика
- 19. Георг Александер Пик родился 10 августа 1859году
- 20. Рассмотрим простой целочисленный многоугольник (все его вершины
- 21. Формула ПикаПлощадь многоугольника с целочисленными вершинами S
- 22. УзелУзел – пересечение двух прямых.A, B – внутренние узлы.C,D – узлы на границе.
- 23. Площадь прямоугольника86S=abS=6 8=48(кв.ед.)По формуле ПикаВ=35; Г= 28S=35+28:2-1=48(кв.ед.)
- 24. Площадь треугольника
- 25. По формуле ПикаВ=25; Г=24S =
- 26. S тр=S пр-(S 1+S 2+S 3)S пр
- 27. 810По формуле ПикаВ = 43;
- 28. Слайд 28
- 29. 1234567891011121011Sпр = 10 11 = 110 (кв.ед.)
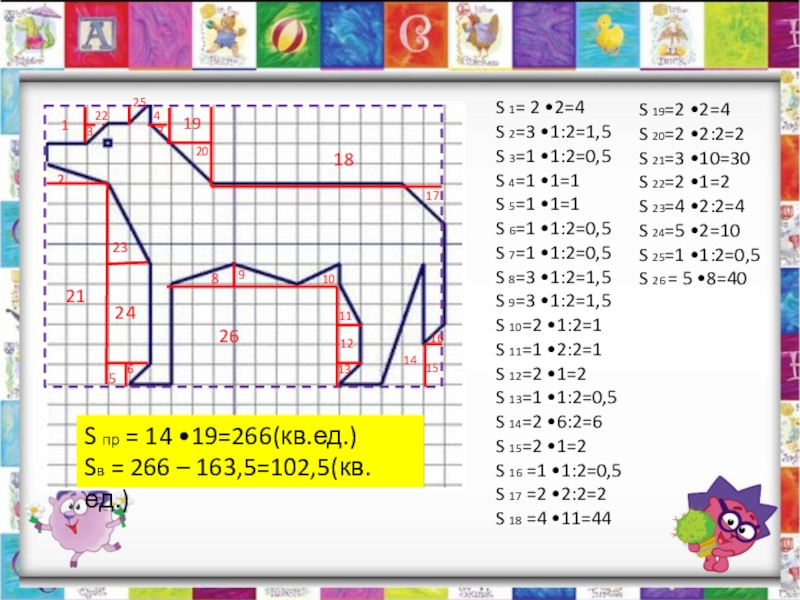
- 30. 1234567891011121314151617181920212223242526S 1= 2 2=4S 2=3 1:2=1,5S 3=1
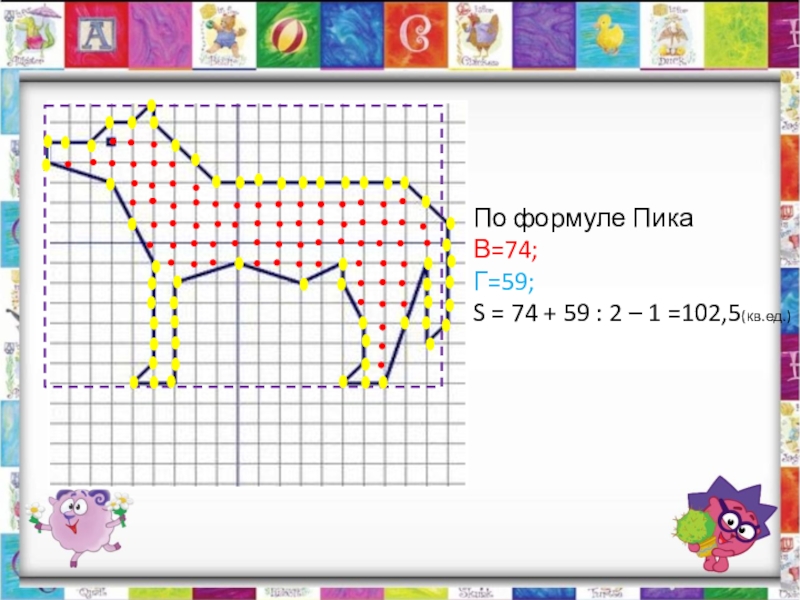
- 31. По формуле ПикаВ=74;Г=59;S = 74 + 59 : 2 – 1 =102,5(кв.ед.)
- 32. Применение формулы Пика
- 33. По формуле ПикаГ =8; В =21;
- 34. Шахматный король обошел доску 8×8 клеток, побывав
- 35. Шахматный король гроссмейстер Михаил Таль в детстве
- 36. Эту формулу можно применять и на практике.
- 37. Задание: Выполнив необходимые расчеты, необходимо благоустроить земельный
- 38. Чертёж должен быть очень четким (для подсчета
- 39. Наблюдение может привести к открытиюЛучший способ изучить
- 40. Работу выполнила ученица 5-А класса Октябрьского УВК №1 «Школа-гимназия»Таминова КаринаРуководитель: Сапунцова Н.Ю.
- 41. Спасибо за внимание
Слайд 1Маленькие секреты клетчатой бумаги
Октябрьский учебно-воспитательный комплекс №1 «Школа-гимназия»
Слайд 3научиться вычислять площади многоугольников с вершинами в узлах клетки.
Цель:
познакомиться с
применение формулы Пика при решении задач
Слайд 4Задачи:
Изучить литературу по данной теме;
2. Рассмотреть различные способы вычислений площадей
3. Показать практическое применение этих способов;
4. Выяснить преимущества и недостатки каждого способа;
5. Систематизировать и углубить накопленные мной знания;
6. Повысить качество знаний и умений;
7. Развивать логическое мышление
Слайд 6Я пишу на бумаге в клетку.
Не люблю я бумагу в строчку.
Вновь
Допишу и поставлю точку.
Не терплю я бумаги писчей.
Чистота, белизна - все скучно!
Мои образы станут пищей
Для поэзии сильной, звучной!
Буквы ровно ложатся редко.
Им вставать! Пробиваться в дамки!
Я пишу на бумаге в клетку.
Я люблю выходить за рамки.
Рубен Кафадарян
Клетчатая бумага, ей посвящают стихи
Слайд 8
Крестики нолики
Правила.
Игра ведется между двумя игроками по классическим правилам:
Игроки ходят по
Побеждает игрок, собравший первым пять или более своих символов в ряд
в любом направлении (по вертикали, по горизонтали или по диагонали).
Слайд 9
Морской бой
Каждый игрок расставляет на поле размером 10х10 клеток свои корабли:
Игрок №1 выбирает произвольную точку на поле, и “стреляет туда”. Естественно, реального расположения кораблей противника он не видит, поэтому рядом со своим полем чертит второе такое же, пустое, где отмечает результаты выстрела: промах или попадание. Игрок №2 выслушивает координаты выстрела (например, Б-5), и сообщает сопернику, попал ли тот (не уточняя, в какой корабль), или промахнулся.
Слайд 10Логическая игра на бумаге "Тупик".
Цель этой игры на бумаге -
Игра ведётся на листе бумаги, на котором ставится несколько рядов точек, например, 4x4. Игроки по очереди соединяют точки отрезками, рисуя ломаную линию, которая не должна себя пересекать и замыкаться. Соединять можно соседние по горизонтали, вертикали и диагонали точки, а также точки, связанные ходом коня, т.е. расположенные на диагонали прямоугольника 1x2. Игрок, который не может сделать ход, проигрывает.
Слайд 11Классические судоку 3х3 Необходимо заполнить свободные клетки цифрами от 1 до 9
Слайд 13Судоку чёт-нечет
В этих судоку содержится дополнительная информация о чётности цифр. То
Слайд 16Основание Карфагена
Об основании древнего города Карфагена существует следующее предание. Дидона, дочь
Слайд 17
Попробуем вычислить, какую площадь могла, согласно этому преданию, занять крепость,
Решение:
Площадь воловьей шкуры 4 кв. м или 4 миллиона кв. мм,
а ширина ремня 1 мм,
то общая длина вырезанного ремня (Дидона, надо думать, вырезала его спирально) — 4 миллиона мм, или 4000 м, то есть 4 км.
Таким ремнем можно окружить квадратный участок в 1 кв. км.
Слайд 19Георг Александер Пик
родился 10 августа 1859
году в Вене
Среди всего многообразия
выделяется формула для вычисления площадей многоугольников с
вершинами в узлах клетки. Она стала широко известна только в 1969 году,
после того, как Гуго Штейнгауз включил ее в свою знаменитую книгу
≪Математический калейдоскоп≫.
Слайд 20Рассмотрим простой целочисленный многоугольник
(все его вершины имеют целые координаты, его
Слайд 21Формула Пика
Площадь многоугольника с целочисленными вершинами
S = В + Г/2
В - количество целочисленных точек внутри многоугольника,
Г — количество целочисленных точек на границе многоугольника
Точка координатной плоскости называется целочисленной, если обе её координаты целые ( т.е. точка находится в узле клетки).
Слайд 23Площадь прямоугольника
8
6
S=ab
S=6 8=48(кв.ед.)
По формуле Пика
В=35; Г= 28
S=35+28:2-1=48(кв.ед.)
Слайд 25По формуле Пика
В=25; Г=24
S = 25+24:2 – 1= 36(кв.ед.)
S=ab:2
S=6
6
12
Прямоугольный треугольник
Слайд 26S тр=S пр-(S 1+S 2+S 3)
S пр = 8 12=96 (кв.ед.)
S
S 2=12 4:2=24 (кв.ед.)
S 3 =4 4:2=8 (кв.ед.)
Sтр =96-(32+8+24)=32 (кв.ед.)
8
12
1
2
3
По формуле Пика
В=25; Г=16;
S= 25+16:2 – 1=32 (кв.ед.)
Произвольный треугольник
Слайд 278
10
По формуле Пика
В = 43; Г=20
S = 43 +
1
2
Sпр =8 10= 80 (кв.ед)
S 1 = 8 3 : 2 = 12 (кв.ед.)
S 2 = 8 4 :2 = 16 (кв.ед)
S тр = 80 – (12+16) = 52 (кв.ед.)
Трапеция
Слайд 291
2
3
4
5
6
7
8
9
10
11
12
10
11
Sпр = 10 11 = 110 (кв.ед.)
S 1= 4
S 2= 4 3 : 2 = 6(кв.ед.)
S 3= 4 1 : 2 = 2(кв.ед.)
S 4= 4 4 = 16(кв.ед.)
S5 = 5 3 : 2 = 7,5(кв.ед.)
S 6= 2 3 = 6(кв.ед.)
S 7= 3 3 : 2 = 4,5(кв.ед.)
S 8= 2 5 : 2 = 5(кв.ед.)
S 9= 4 1 : 2 = 2 (кв.ед.)
S 10= 4 1 = 4(кв.ед.)
S 11= 3 2 : 2 = 3(кв.ед.)
S 12= 2 2 : 2 = 2(кв.ед.)
S зв= 110-70 = 40(кв.ед.)
По формуле Пика
В=31; Г=20
S= 31+20:2-1=40(кв.ед.)
Слайд 301
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
S 1= 2 2=4
S 2=3 1:2=1,5
S 3=1 1:2=0,5
S 4=1 1=1
S 5=1
S 6=1 1:2=0,5
S 7=1 1:2=0,5
S 8=3 1:2=1,5
S 9=3 1:2=1,5
S 10=2 1:2=1
S 11=1 2:2=1
S 12=2 1=2
S 13=1 1:2=0,5
S 14=2 6:2=6
S 15=2 1=2
S 16 =1 1:2=0,5
S 17 =2 2:2=2
S 18 =4 11=44
S 19=2 2=4
S 20=2 2:2=2
S 21=3 10=30
S 22=2 1=2
S 23=4 2:2=4
S 24=5 2=10
S 25=1 1:2=0,5
S 26 = 5 8=40
S пр = 14 19=266(кв.ед.)
Sв = 266 – 163,5=102,5(кв.ед.)
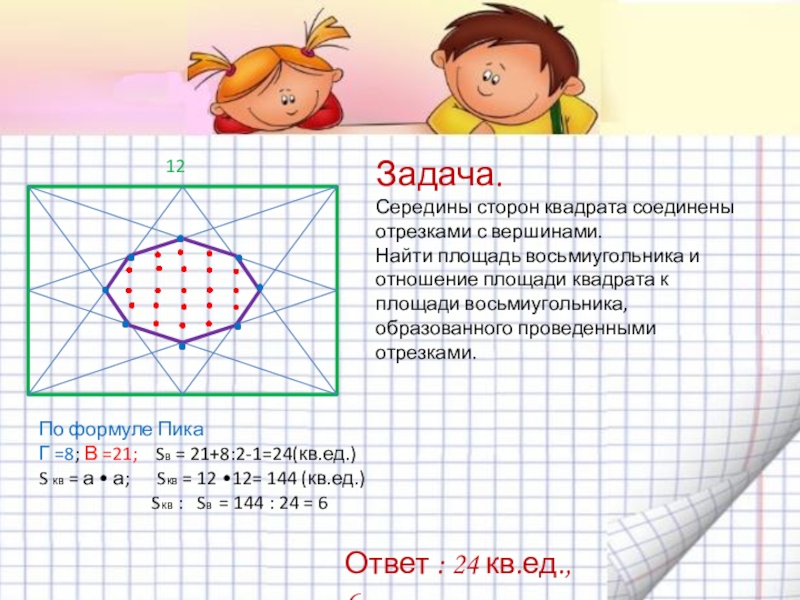
Слайд 33По формуле Пика
Г =8; В =21; Sв = 21+8:2-1=24(кв.ед.)
S кв
Sкв : Sв = 144 : 24 = 6
Задача.
Середины сторон квадрата соединены отрезками с вершинами.
Найти площадь восьмиугольника и отношение площади квадрата к
площади восьмиугольника, образованного проведенными отрезками.
Ответ : 24 кв.ед., 6
12
Слайд 34Шахматный король обошел доску 8×8 клеток, побывав на
каждом поле ровно один
ограничивать эта ломаная? (Сторона клетки равна 1.)
По формуле Пика:
В=0; Г=64; S = 0 + 64 : 2 – 1 = 31
Так как узлами решетки служат центры 64 полей и, по условию, все они лежат на границе многоугольника. Таким образом, хотя таких траекторий короля достаточно много, но все они ограничивают многоугольники равных площадей.
Слайд 35Шахматный король гроссмейстер Михаил Таль в детстве был потрясен доказательством теоремы,
Нарисуем на шахматной доске квадрат (Рис. 1).
Доска разбивается на пять частей – сам квадрат и четыре одинаковых прямоугольных треугольника.
А теперь посмотрим на рисунок 2. здесь те же четыре треугольника, а вместо одного квадрата уже два, но меньшего размера.
Треугольники на обоих рисунках одни и те же, а, значит, их площади равны. Следовательно, равную площадь занимают и оставшиеся части доски: на первом рисунке один квадрат, на втором – два. Поскольку большой квадрат построен на гипотенузе прямоугольного треугольника, а маленькие – на его катетах, получаем, что квадрат гипотенузы равен сумме квадратов катетов.
Рисунок 1
Рисунок 2
Слайд 36Эту формулу можно применять и на практике. Фигуру, площадь которой требуется
Существуют и механические приборы для вычисления площадей плоских фигур так называемые планиметры.
Слайд 37Задание:
Выполнив необходимые расчеты, необходимо благоустроить земельный участок для высадки цветов:
-
- Найти его площадь;
- Рассчитайте количество цветочной рассады, если на 1 кв.м. рекомендуют высаживать 50 шт. бархатцев «Золото маккены». Удобрение «Кимира универсал – 2», расход 100 г. на 1 кв.м
План:
На миллиметровой бумаги начертим форму клумбы.
Примем 1 см на бумаге равным 1 м в реальности.
Найдем площадь фигуры.
Рассчитаем количество цветочной рассады.
Рассчитаем удобрение.
Слайд 38Чертёж должен быть очень четким
(для подсчета узлов)
Формула применяется лишь в
Недостатки формулы Пика
Узкий спектр задач
Слайд 39Наблюдение может привести к открытию
Лучший способ изучить что-либо – открыть это
Выводы
Нужно отыскать в задаче то, что может пригодиться при решении других задач (т.е. обнаружить общий метод)