- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Линии на плоскости
Содержание
- 1. Презентация по математике на тему Линии на плоскости
- 2. Линия на плоскости – множество
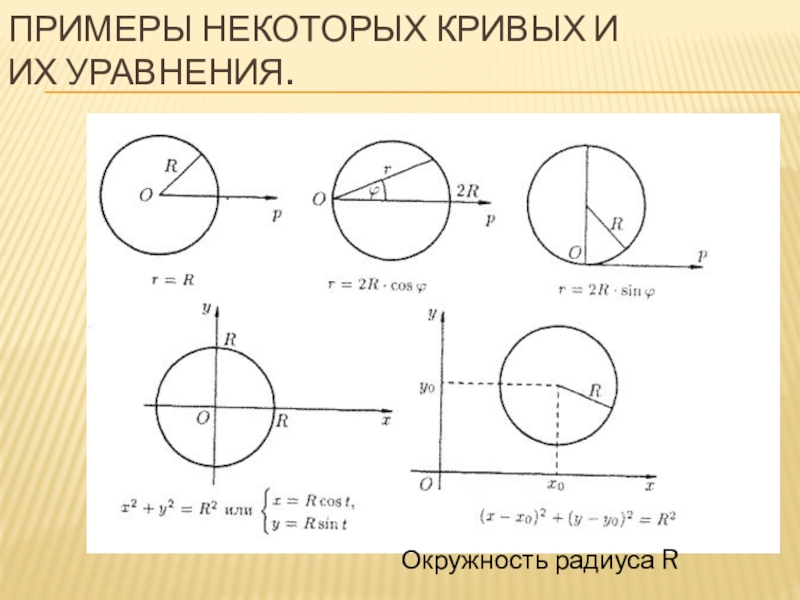
- 3. примеры некоторых кривых и их уравнения.Окружность радиуса R
- 4. Лемниската Бернулли Лемниската Бернулли- плоская алгебраическая
- 5. Уравнения Лемниската Бернулли Рассмотрим простейший случай:
- 6. ПостроенияПостроение лемнискаты при помощи секущихШарнирный методМеханизм Ватта (анимация)Другой вариант шарнирного метода
- 7. улитка паскаля Улитка Паскаля ― плоская
- 8. УравненияУравнение в прямоугольных координатах: в полярных координатах:
- 9. Полукубическая парабола Полукубическая парабола, или парабола
- 10. Астроида Астроида— плоская кривая, описываемая точкой
- 11. УравненияУравнение в декартовых прямоугольных координатах:Параметрическое уравнение:Уравнение в рациональном виде:
- 12. Кардиоида Кардиоида— плоская линия, которая описывается
- 13. Уравнения Пусть - радиус окружностей,
- 14. Архимедова спираль Архимедова спираль —
- 15. Циклоида Циклоида— плоская трансцендентная кривая. Циклоида
- 16. Слайд 16
Линия на плоскости – множество точек плоскости, обладающих некоторым только им присущим геометрическим свойством. Введение на плоскости системы координат позволяет определять положение точки плоскости заданием двух чисел — ее координат, а положение линии
Слайд 2 Линия на плоскости – множество точек плоскости, обладающих некоторым
только им присущим геометрическим свойством.
Введение на плоскости системы координат позволяет определять положение точки плоскости заданием двух чисел — ее координат, а положение линии на плоскости определять с помощью уравнения
Уравнением линии (или кривой) на плоскости Оху называется такое уравнение F(x;y) = 0 с двумя переменными, которому удовлетворяют координаты x и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Введение на плоскости системы координат позволяет определять положение точки плоскости заданием двух чисел — ее координат, а положение линии на плоскости определять с помощью уравнения
Уравнением линии (или кривой) на плоскости Оху называется такое уравнение F(x;y) = 0 с двумя переменными, которому удовлетворяют координаты x и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Слайд 4Лемниската Бернулли
Лемниската Бернулли- плоская алгебраическая кривая. Определяется как геометрическое
место точек,произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами.
Слайд 5Уравнения Лемниската Бернулли
Рассмотрим простейший случай: если расстояние между фокусами
, расположены они на оси , и начало координат делит отрезок между ними пополам, то следующие уравнения задают лемнискату:
В прямоугольных координатах:
В полярных координатах:
Параметрическое уравнение в прямоугольной системе:
В прямоугольных координатах:
В полярных координатах:
Параметрическое уравнение в прямоугольной системе:
, где
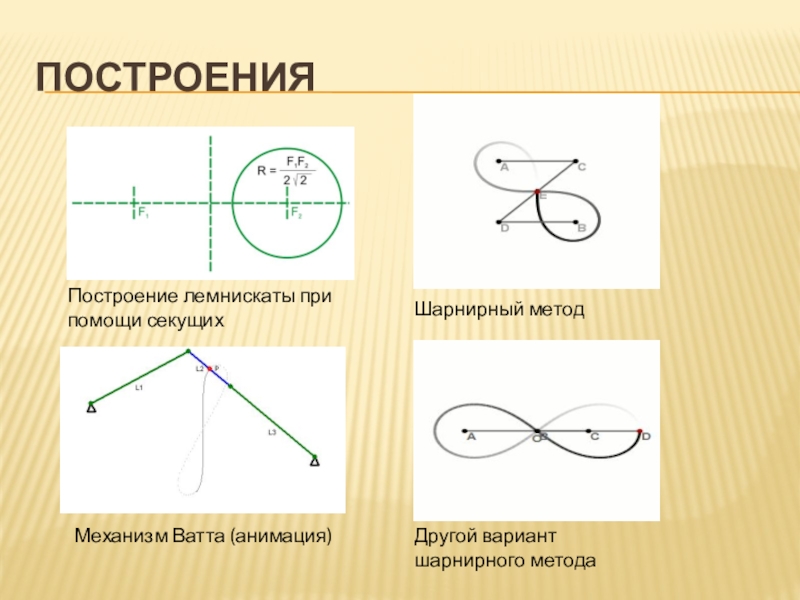
Слайд 6Построения
Построение лемнискаты при помощи секущих
Шарнирный метод
Механизм Ватта (анимация)
Другой вариант шарнирного метода
Слайд 7улитка паскаля
Улитка Паскаля ― плоская алгебраическая кривая 4-го порядка;
подера окружности, конхоида окружности относительно точки на окружности, частный случай Декартова овала, она также является эпитрохоидой.
Слайд 8Уравнения
Уравнение в прямоугольных координатах:
в полярных координатах:
Здесь a — диаметр
исходной окружности, а l — расстояние, на которое смещается точка вдоль радиус-вектора.
Слайд 9Полукубическая парабола
Полукубическая парабола, или парабола Нейла — плоская алгебраическая
кривая, описываемая уравнением y2=ax3 в некоторой прямоугольной системе координат.
Уравнения
Алгебраическое уравнение: y2=ax3 (a≠0).
Параметрическое уравнение: x=t2, y=at3 (a≠0).
Уравнения
Алгебраическое уравнение: y2=ax3 (a≠0).
Параметрическое уравнение: x=t2, y=at3 (a≠0).
Слайд 10Астроида
Астроида— плоская кривая, описываемая точкой
окружности радиуса
r,
катящейся по внутренней
стороне окружности радиуса R=4r. Иначе говоря, астроида — это гипоциклоида с модулем k=4.
катящейся по внутренней
стороне окружности радиуса R=4r. Иначе говоря, астроида — это гипоциклоида с модулем k=4.
Слайд 11Уравнения
Уравнение в декартовых прямоугольных координатах:
Параметрическое уравнение:
Уравнение в рациональном виде:
Слайд 12Кардиоида
Кардиоида— плоская линия, которая описывается фиксированной точкой окружности, катящейся
по неподвижной окружности с таким же радиусом. Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.
Слайд 13Уравнения
Пусть - радиус окружностей, начало координат находится в
конечной точке горизонтального диаметра неподвижной окружности. Тогда уравнения кардиоиды можно записать в следующих формах.
В прямоугольных координатах:
В прямоугольных координатах (параметрическая запись):
В полярных координатах:
В прямоугольных координатах:
В прямоугольных координатах (параметрическая запись):
В полярных координатах:
Слайд 14Архимедова спираль
Архимедова спираль — спираль, плоская кривая, траектория
точки M, которая равномерно движется вдоль луча OV с началом в O, в то время как сам луч OV равномерно вращается вокруг O. Другими словами, расстояние ρ = OM пропорционально углу поворота φ луча OV. Повороту луча OV на один и тот же угол соответствует одно и то же приращение ρ.
Уравнение Архимедовой спирали в полярной системе координат записывается так:
где k — смещение точки M по лучу r, при повороте на угол равный одному радиану.
Повороту прямой на соответствует смещение a = |BM| = |MA| = . Число a — называется шагом спирали. Уравнение Архимедовой спирали можно переписать так:
Уравнение Архимедовой спирали в полярной системе координат записывается так:
где k — смещение точки M по лучу r, при повороте на угол равный одному радиану.
Повороту прямой на соответствует смещение a = |BM| = |MA| = . Число a — называется шагом спирали. Уравнение Архимедовой спирали можно переписать так:
Слайд 15Циклоида
Циклоида— плоская трансцендентная кривая. Циклоида определяется кинематически как траектория
фиксированной точки производящей окружности радиуса , катящейся без скольжения по прямой.
Уравнения:
Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса .
Циклоида описывается параметрически,
.
Уравнение в декартовых координатах:
Циклоида может быть получена как решение дифференциального уравнения:
Уравнения:
Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса .
Циклоида описывается параметрически,
.
Уравнение в декартовых координатах:
Циклоида может быть получена как решение дифференциального уравнения: