- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Комбинаторика
Содержание
- 1. Презентация по математике на тему Комбинаторика
- 2. Слайд 2
- 3. Комбинаторика Термин «комбинаторика» происходит от латинского слова
- 4. Комбинаторика
- 5. Области применения комбинаторики: учебные заведения (составление расписаний)сфера общественного питания (составление меню)
- 6. Области применения комбинаторики:
- 7. география (раскраска карт)Биология (расшифровка кода ДНК)производство (распределение
- 8. азартные игры (подсчёт частоты
- 9. доставка почты (рассмотрение вариантов пересылки) военное дело (расположение подразделений)астрология (анализ расположения планет и созвездий)
- 10. Из истории комбинаторики
- 11. Бхаскара
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Пьер ФермаБлез Паскаль
- 18. Яков БернуллиГотфрид Вильгельм Лейбниц Леонард Эйлер
- 19. (1.07.1646 - 14.11.1716)Готфрид Вильгельм Лейбниц
- 20. Леонард Эйлер
- 21. Якоб Бернулли (1654-1705)
- 22. Слайд 22
- 23. Правила суммы и произведения
- 24. ПРАВИЛО СУММЫЕсли некоторый объект A можно выбрать
- 25. Пример:Ученик должен выполнить практическую работу по математике.
- 26. ПРАВИЛО ПРОИЗВЕДЕНИЯЕсли объект А можно выбрать из
- 27. Примеры задач. 1.Переплетчик должен переплести 12 различных
- 28. ФАКТОРИАЛ ЧИСЛАФакториал числа — это произведение всех
- 29. Значения факториалов от 0 до 100!
- 30. Свойство факториала: (n + 1)! = (n
- 31. Комбинаторные соединения
- 32. Комбинаторные соединенияКомбинаторные соединения— это такие комбинации из каких-либо элементов.
- 33. Типы соединений: ПерестановкиРазмещения
- 34. ПЕРЕСТАНОВКИПерестановки без повторений — комбинаторные соединения,
- 35. Пример. Сколькими способами семь книг
- 36. Перестановки с повторениями Это комбинаторные соединения,
- 37. Формула для нахождения количества перестановок с повторениями:
- 38. Пример. Сколькими способами можно переста-
- 39. РАЗМЕЩЕНИЯРазмещения без повторений — комбинаторные соединения, составленные
- 40. Формула для нахождения количества размещений без повторений:
- 41. Размещения с повторениямиЭто— комбинаторные соединения, составленные из
- 42. СОЧЕТАНИЯСочетания без повторений — комбинаторные соединения из
- 43. Формула для нахождения количества сочетаний без повторений:
- 44. Сочетания с повторениями Это— комбинаторные соединения
- 45. Задачи по комбинаторике
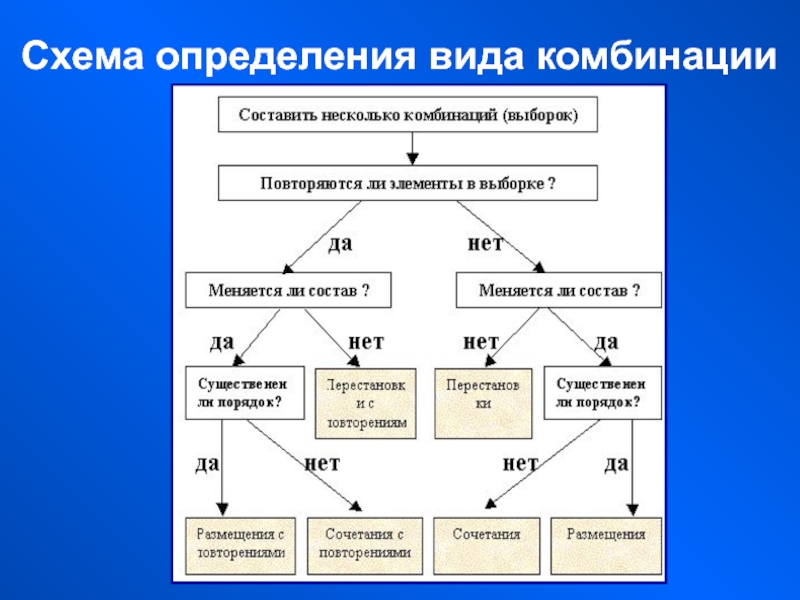
- 46. Схема определения вида комбинации
- 47. Пример
- 48. Правило суммыЗадача. Имеется 5 билетов денежно-вещевой
- 49. Правило произведение Задача. В школьной столовой имеются
- 50. Размещения без повторений Задача. Сколькими способами 4
- 51. Перестановки без повторенийЗадача. Сколько различных шестизначных
- 52. Сочетания без повторений Задача №1Сколько трехкнопочных комбинаций
- 53. Задача №2 У одного
- 54. Решение задач на сочетание, размещение, перестановки с повторениями
- 55. Размещение с повторением ЗадачаСколько трехзначных чисел можно
- 56. Задача №2 В кондитерском магазине продавались 4
- 57. Задача №3 У мамы 2 яблока, 3
- 58. Задача Имеются в неограниченном количестве палочки
- 59. Комбинаторика
Слайд 3Комбинаторика
Термин «комбинаторика» происходит от латинского слова «combina», что в
Комбинато́рика— раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка).
Слайд 5Области применения комбинаторики:
учебные заведения (составление расписаний)
сфера общественного питания
(составление меню)
Слайд 6
Области применения комбинаторики:
лингвистика (рассмотрение вариантов комбинаций букв)
спортивные соревнования (расчёт количества игр между участниками)
Слайд 7география (раскраска карт)
Биология (расшифровка кода ДНК)
производство (распределение нескольких видов работ между
агротехника (размещение посевов на нескольких полях)
Слайд 8 азартные игры (подсчёт частоты выигрышей)
химия (анализ возможных связей
экономика (анализ вариантов купли-продажи акций)
Криптография
(разработка методов
шифрования)
Слайд 9доставка почты (рассмотрение вариантов пересылки)
военное дело (расположение
астрология (анализ расположения планет и созвездий)
Слайд 24ПРАВИЛО СУММЫ
Если некоторый объект A можно выбрать m способами, а другой
Если конечные множества не пересекаются, то число элементов X U Y {или} равно сумме числа элементов множества X и числа элементов множества Y.
Слайд 25Пример:
Ученик должен выполнить практическую работу по математике. Ему предложили
Сколькими способами он может выбрать одну тему для практической работы?
Решение: X=17, Y=13
По правилу суммы X U Y=17+13=30 тем.
Слайд 26ПРАВИЛО ПРОИЗВЕДЕНИЯ
Если объект А можно выбрать из совокупности объектов m способами
Слайд 27Примеры задач.
1.Переплетчик должен переплести 12 различных книг в красный, зеленый
Решение: Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12*3=36 вариантов переплета.
2 . Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя - как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z -любые цифры, а X - не ноль.
Значит по правилу произведения количество цифр, одинаково читающихся как слева направо, так и справа налево, равно 9*10*10=900 вариантов.
Слайд 28ФАКТОРИАЛ ЧИСЛА
Факториал числа — это произведение всех натуральных чисел до этого
Обозначается с восклицательным знаком в конце.
n! = 1 · 2 · 3 · 4 · … · (n-2) · (n-1) · n
Слайд 29Значения факториалов
от 0 до 10
0! = 1
1! = 1
2! =
3! = 1 · 2 · 3 = 6
4! = 1 · 2 · 3 · 4 = 24
5! = 1 · 2 · 3 · 4 · 5 = 120
6! = 1 · 2 · 3 · 4 · 5 · 6 = 720
7! = 1 · 2 · 3 · 4 · 5 · 6 · 7 = 5040
8! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 = 40320
9! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 = 362880
10! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 = 3628800
Слайд 30Свойство факториала:
(n + 1)! = (n + 1) · n!
Например:
(5 +
Действительно
6! = (1 · 2 · 3 · 4 · 5) · 6 = 720,
А значение (1 · 2 · 3 · 4 · 5) = 5! = 120
120 · 6=720
Слайд 32Комбинаторные соединения
Комбинаторные соединения— это такие комбинации из каких-либо элементов.
Слайд 33
Типы соединений:
Перестановки
Размещения
Сочетания
Две схемы выбора
Без повторений
С повторениями
Слайд 34 ПЕРЕСТАНОВКИ
Перестановки без повторений — комбинаторные соединения, состоящие из одних и
Формула для нахождения количества перестановок без повторений:
Pn = n!
где n! = 1 * 2 * 3 ... n.
Слайд 35Пример.
Сколькими способами семь
книг разных авторов можно
ряд? Решение:
эта задача о числе перестановок семи разных книг. Имеется P7=7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.
Слайд 36
Перестановки с повторениями
Это комбинаторные соединения, в которых среди образующих элементов имеются
Слайд 38Пример.
Сколькими способами можно переста-
вить буквы слова «ананас»?
Решение:
n1 «а»=3, n2 «н» =2, n3 «с»=1.
Следовательно, число различных перестановок равно:
Ответ: 60 способов.
Слайд 39РАЗМЕЩЕНИЯ
Размещения без повторений — комбинаторные соединения, составленные из n различных элементов
Слайд 41
Размещения с повторениями
Это— комбинаторные соединения, составленные из n элементов по m.
Формула для нахождения количества размещений с повторениями:
Слайд 42СОЧЕТАНИЯ
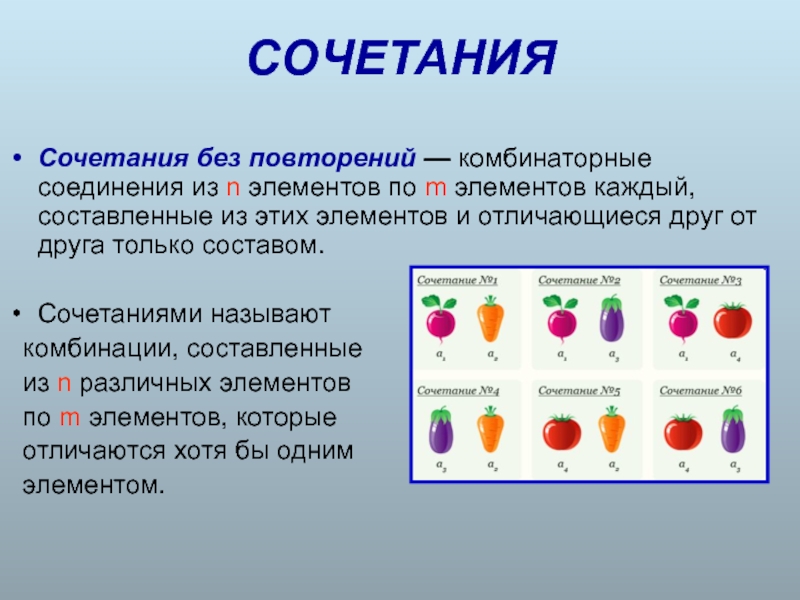
Сочетания без повторений — комбинаторные соединения из n элементов по m
Сочетаниями называют
комбинации, составленные
из n различных элементов
по m элементов, которые
отличаются хотя бы одним
элементом.
Слайд 44Сочетания с повторениями
Это— комбинаторные соединения из n
Формула для нахождения количества сочетаний с повторениями:
Слайд 47Пример
В магазине
Решение: Обозначив игрушки первыми буквами названия, составим несколько комбинаций: КЧЧЧЧЧЧЧК, ЧЧЧКЧКЧЧЧ, ККЧЧЧЧЧЧЧ, ...
Повторяются ли элементы в выборке? - Да.
Меняется ли состав? - Нет, ведь каждая выборка состоит из семи букв "Ч" и двух букв "К".
Следовательно, это перестановки с повторениями.
Ответ: 36 способами.
Слайд 48Правило суммы
Задача.
Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото
Решение: Так как денежно-вещевая лотерея в выборе не участвует, то всего 6+10=16 вариантов.
Ответ: 16 вариантов
Слайд 49Правило произведение
Задача.
В школьной столовой имеются 2 первых, 5 вторых и
Решение: Согласно правилу умножения таких обедов можно составить 2×5×4 = 40 способами.
Ответ:40 вариантов обедов.
Слайд 50Размещения без повторений
Задача.
Сколькими способами 4 юноши могут пригласить четырех из
Решение: два юноши не могут одновременно пригласить одну и ту же девушку. И варианты, при которых одни и те же девушки танцуют с разными юношами, считаются разными, поэтому:
Воспользуемся формулой
Ответ: Возможно 360 вариантов.
Слайд 51Перестановки без повторений
Задача.
Сколько различных шестизначных чисел можно составить из
Решение:
1) Найдем количество всех перестановок из этих цифр:
P6=6!=720
2) 0 не может стоять впереди числа, поэтому от этого числа необходимо отнять количество перестановок, при котором 0 стоит впереди.
P5=5!=120.
P6-P5=720-120=600 перестановок
Ответ: 600
Слайд 52Сочетания без повторений
Задача №1
Сколько трехкнопочных комбинаций
существует на кодовом замке
(все
если на нем всего 10 цифр.
Решение:
Так как кнопки нажимаются одновременно, то выбор этих трех кнопок – сочетание. Отсюда возможно
Ответ: 120 вариантов
Слайд 53Задача №2
У одного человека 7 книг по математике,
Решение:
Так как надо порядок следования книг не имеет значения, то выбор 2-ух книг - сочетание. Первый человек может выбрать 2 книги
способами
Второй человек может выбрать 2 книги
способами
Значит всего по правилу произведения возможно 21*36=756 вариантов.
Ответ: 756 способов.
Слайд 55Размещение с повторением
Задача
Сколько трехзначных чисел можно составить из цифр 1,
Решение. Так как порядок цифр в числе существенен, цифры могут повторяться, то это будут размещения с повторениями из пяти элементов по три. Воспользуемся формулой
Получим
Ответ: 125 чисел.
Слайд 56Задача №2
В кондитерском магазине продавались 4 сорта пирожных: эклеры, песочные, наполеоны
Решение: Покупка не зависит от того, в каком порядке укладывают купленные пирожные в коробку. Покупки будут различными, если они отличаются количеством купленных пирожных хотя бы одного сорта. Следовательно, количество различных покупок равно числу сочетаний четырех видов пирожных по семь -
Ответ: 120 способов.
Слайд 57Задача №3
У мамы 2 яблока, 3 груши и 4 апельсина.
Решение Обозначая фрукты по первым буквам названия, составим несколько вариантов выдачи: ЯЯГГГАААА, ААГГЯГААЯ, ГГГААЯЯАА. Эти выборки имеют один и тот же состав и отличаются только перестановкой элементов, поэтому применяем формулу числа перестановок с повторениями
Ответ: 1260 вариантов
Слайд 58Задача
Имеются в неограниченном количестве палочки длиной 5, 6, 7,
Решение. Составим несколько выборок: (5,5,5); (6,7,8); (8,9,9).. Элементы повторяются, состав меняется, порядок не существенен. Согласно схеме, применяем формулу сочетаний с повторениями из 6 по 3:
Однако здесь есть небольшой подвох: треугольника со сторонами 5, 5, 10 не существует, так что их будет
56-1=55.
Ответ: 55 треугольников