Учитель математики: Глебова Любовь Николаевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Классическое определение вероятности
Содержание
- 1. Презентация по математике на тему Классическое определение вероятности
- 2. Цель урока: рассмотреть простейшие понятия теории вероятностей.План
- 3. 3.1. Что изучает теория вероятностей.Теория вероятностей – это раздел
- 4. Краткая историческая справкаКак наука теория вероятности зародилась
- 5. Но при этом честь открытия этой теории,
- 6. Во второй половине XIX века основной вклад
- 7. Первичные понятия теории вероятностейОпыт (испытание) – это производимые
- 8. Два события, которые в данных условиях могут
- 9. Равновозможными называются события, когда в их наступлении
- 10. Событие, которое происходит всегда, называют достоверным событием.Вероятность
- 11. Что такое «теория вероятностей»? Теория вероятностей –
- 12. Классическое определение вероятности.
- 13. 3) частное
- 14. Слайд 14
- 15. Пример.
- 16. Правило умножения: для того, чтобы найти
- 17. События А и В называются противоположными, если
- 18. В среднем из 1000 аккумуляторов, поступивших в
- 19. Решение задач.1. Автомобиль проезжает мимо светофора два
- 20. 2. У Маши сломался автомобиль, она набирает номер
- 21. 3. В фирме такси 6 красных и
- 22. 4. Научная конференция проводится 3 дня. Всего
- 23. 5. Перед началом первого тура чемпионата по
- 24. Решение задач в группах 1. В двигатели
- 25. Решения к задачам1. Общее число элементарных событий
- 26. 3.Элементарный исход в этом опыте – порядочная
- 27. 4. Всего билетов N=4+7+9+5+5=25. Событию А =
- 28. Итог урокаДомашнее задание:Придумать 5 задач, связанных с профессией автомеханик, на нахождение классической вероятности.
- 29. 1. А.Г.Мордкович. Алгебра и начала математического анализа.
Слайд 1
ТЕМА УРОКА:
«КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ».
ГБПОУ РО
ПРОМЫШЛЕННО-ПОЛИГРАФИЧЕСКОЕ ПРОФЕССИОНАЛЬНОЕ УЧИЛИЩЕ №
Слайд 2
Цель урока: рассмотреть простейшие понятия теории вероятностей.
План урока:
1) Организационный момент.
2) Повторение
3) Изучение нового материала.
3.1. Что изучает теория вероятностей.
3.2. Краткая историческая справка.
3.3. Что такое теория вероятностей?
3.4. Решение простейших вероятностных задач.
4) Итоги урока.
5) Домашнее задание.
Слайд 33.1. Что изучает теория вероятностей.
Теория вероятностей – это раздел математической науки, изучающий закономерности
Теория вероятностей применима в робототехнике. Например, некое автоматизированное устройство (первичная заготовка робота) выполняет определенные вычисления. В то время как она ведет расчеты, снаружи на нее систематически воздействуют различными помехами, незначительными для системы, но сказывающимися на результатах работы. Задача инженера состоит в том, чтобы определить, с какой частотой будет возникать ошибка, навязанная внешними помехами. Так же методами теории вероятности возможно разработать алгоритм для сведения погрешности вычисления к минимуму. Задачи подобного рода очень часто встречаются в физике и при разработке новых видов техники. Они требуют тщательного изучения не только главных закономерностей объясняющих основные черты данных явлений в общих их понятиях, но и анализа случайных искажений и возмущений, связанных с действием второстепенных факторов, которые придают исходу опыта в заданных условиях тот самый элемент случайности (неопределенности).
Слайд 4Краткая историческая справка
Как наука теория вероятности зародилась в 17в. Появление понятия
Схема азартных игр была очень проста и могла быть подвергнута всестороннему логическому анализу. Первые попытки этого рода связаны с именами известных учёных – алгебраиста Джероламо Кардано (1501 – 1576) и Галилео Галилея (1564 – 1642).
Д. Кардано
Г. Галилей
Слайд 5Но при этом честь открытия этой теории, которая не только предоставляет
Б. Паскаль
П.Ферма
Слайд 6Во второй половине XIX века основной вклад внесли русские учёные П.
П.Л.Чебышев
А.А.Марков
А.М.Ляпунов
А.Н.Колмогоров
Слайд 7Первичные понятия теории вероятностей
Опыт (испытание) – это производимые действия.
Событие – это результат опыта.
Какое-либо
В жизни мы постоянно сталкиваемся с тем, что некоторое событие может произойти, а может и не произойти.
НАПРИМЕР: В 12.00 по мосту проедет красная машина. Перед машиной пробежит черная кошка. При бросании кубика выпадет тройка.
Слайд 8Два события, которые в данных условиях могут происходить одновременно, называются совместными,
Примеры.
1. Из ящика с деталями наудачу извлечена деталь. Появление стандартной детали исключает появление нестандартной детали. События «появилась стандартная деталь» и «появилась нестандартная деталь» - несовместные.
2. Брошена монета. Появление орла исключает появление решки. События «появился орел» и «появилась решка» - несовместные.
3. Примеры ребят.
Слайд 9Равновозможными называются события, когда в их наступлении нет преимуществ.
Неравновозможные события
Примеры.
Появление орла или решки при бросании монеты представляют собой равновероятные события.
2. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно).
3. Примеры ребят.
Слайд 10Событие, которое происходит всегда, называют достоверным событием.
Вероятность достоверного события равна 1.
Событие, которое не может произойти, называется невозможным.
Вероятность невозможного события равна 0.
Примеры.
1. Машина заведется без аккумулятора. При бросании кубика выпадет семерка. Это невозможные события.
2. Машина заведется с аккумулятором. При бросании кубика выпадет число, меньше семи. Это достоверные события.
3. Пусть, например, в автосалоне продаются только белые автомобили, продают один. Тогда продажа белого автомобиля – достоверное событие; продажа черного автомобиля – невозможное событие.
Слайд 11Что такое «теория вероятностей»?
Теория вероятностей – раздел математики, изучающий закономерности
Теория вероятностей – это математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким – либо образом с первыми. (А.А.Боровков «Теория вероятностей», М.: Наука, 1986 год.)
Вероятность – это численная характеристика реальности появления того или иного события.
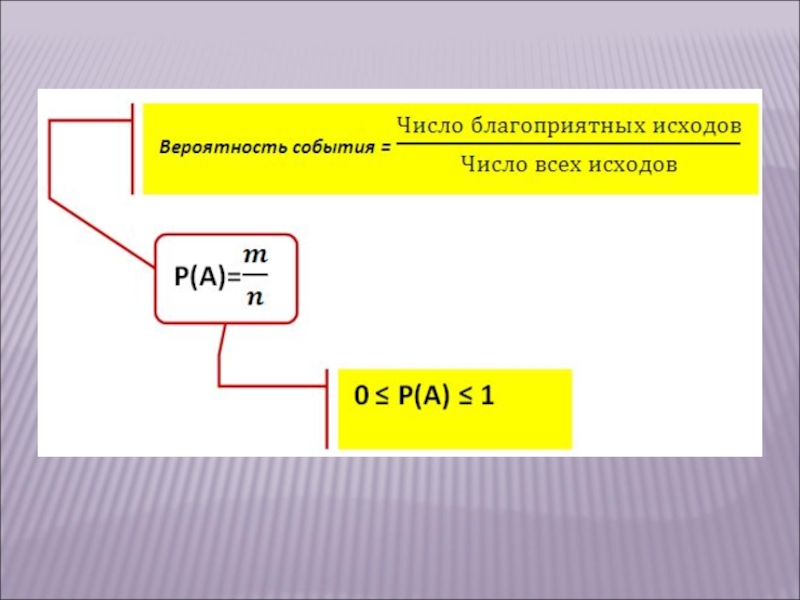
Слайд 12Классическое определение вероятности.
Вероятностью события А
Слайд 13
3) частное
Значит
Алгоритм нахождения вероятности
случайного события.
Для нахождения вероятности случайного события А при проведении некоторого испытания следует найти:
1) число N всех возможных исходов данного испытания;
2) количество N(A) тех исходов, в которых наступает событие А;
Принято вероятность события А обозначать так: Р(А).
Слайд 15
Пример.
На завод привезли партию
Благоприятное событие А: подшипник окажется стандартным.
Решение.
Количество всех возможных исходов
N = 1000.
Количество благоприятных исходов N(A)=1000-30=970.
Значит:
Ответ: 0.97.
Слайд 16 Правило умножения: для того, чтобы найти число всех
Пример.
Найдем вероятность того, что при подбрасывании двух костей суммарное число очков окажется равным 5.
Благоприятное событие А: в сумме выпало 4 очка.
Количество всех возможных исходов:
Кол-во благоприятных исходов N(A)=
1-я кость - 6 вариантов
2-я кость - 6 вариантов
N=6∙6=36.
{1 + 4, 2 + 3, 3 + 2, 4 + 1}=4
Решение:
Значит:
Ответ:
Слайд 17События А и В называются противоположными,
если всякое наступление события А
ненаступление события В, а ненаступление события А – наступление события В.
Пример.
Бросаем один раз игральную кость.
Событие А – выпадение четного числа очков,
Событие Ā - выпадение нечетного числа очков.
При решении некоторых задач удобно использовать свойство вероятностей противоположных событий
Событие, противоположное событию А,
обозначают символом
Сумма вероятностей противоположных
событий равна 1.
Слайд 18В среднем из 1000 аккумуляторов, поступивших в продажу, 6 неисправны. Найдите
Решение. Элементарный исход – случайно выбранный аккумулятор. Поэтому
N = 1000.
Событию А = {аккумулятор исправен} благоприятствуют
1000 – 6 = 994 исхода.
Поэтому N(A) = 994.
Тогда
Ответ: 0,994.
Эту задачу можно решить с помощью формулы вероятности
противоположного события
= {аккумулятор неисправен}. Тогда N(Ā)=6.
Имеем
=
Значит, P(A) = 1-
=1 – 0,006 = 0,994. Ответ: 0,994.
Слайд 19Решение задач.
1. Автомобиль проезжает мимо светофора два раза, какова вероятность того
б) Пусть В - событие, состоящее в том, что в результате проведенного испытания оба раза, будет гореть зеленый.
Событию В благоприятствует один исход ЗЗ, т.е. N(B) = 1. Следовательно,
а) Пусть А - событие, состоящее в том, что в результате проведенного испытания хотя бы один раз, будет гореть зеленый?
Равновозможными элементарными исходами здесь
являются: КЗ, КЖ, КК, ЗК, ЗЖ, ЗЗ, ЖК, ЖЗ, ЖЖ, т.е. N = 9. Событию А благоприятствуют исходы: КЗ,ЗК, ЗЖ, ЗЗ, ЖЗ, т.е. N(A) = 5.
Следовательно,
Решение.
Слайд 202. У Маши сломался автомобиль, она набирает номер автосервиса, но понимает, что
Общее число элементарных исходов равно N = 10 .
Событию А благоприятствует одна цифра, N(А) = 1.
Следовательно,
.
Решение.
Слайд 213. В фирме такси 6 красных и 6 желтых автомобилей. На
Решение.
Р(А) = 0, т.к. это событие А - невозможное.
Ответ: 0.
Слайд 224. Научная конференция проводится 3 дня. Всего запланировано 50 докладов: в
Так как в третий день будут слушать 10 докладов, то благоприятных исходов N(А) = 10, а всего докладов 50, т.е. равновозможных исходов N = 50. Поэтому
.
Решение.
Слайд 235. Перед началом первого тура чемпионата по автогонкам разбивают на игровые
Число всех исходов N = 50. Число элементарных событий, благоприятствующих событию А равно 15. Все элементарные события равновозможные по условию задачи, поэтому
Решение.
Слайд 24Решение задач в группах
1. В двигатели автомобиля 4 свечи зажигания,
2. В автосервисе стоят 6 поломанных автомобилей: 1- ГАЗ2. В автосервисе стоят 6 поломанных автомобилей: 1- ГАЗ, 2- ВАЗ (LADA)2. В автосервисе стоят 6 поломанных автомобилей: 1- ГАЗ, 2- ВАЗ (LADA), 1- УАЗ, 1 - Ford2. В автосервисе стоят 6 поломанных автомобилей: 1- ГАЗ, 2- ВАЗ (LADA), 1- УАЗ, 1 - Ford,1- Chevrolet. Найдите вероятность того, что первыми сделают иномарки.
3. В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет 8 очков.
4. На экзамене по автомеханике в 4 билетах встречается вопрос про трансмисси4. На экзамене по автомеханике в 4 билетах встречается вопрос про трансмиссию, 7 билетов про двигатель, 9 билетов про ходовую часть и 5- про электрооборудование. Студент выучил все билеты про ходовую часть автомобиля. Найдите вероятность того, что билет, который он вытянет, окажется про ходовую часть автомобиля.
5. В чемпионате России по автогонкам участвует 20 спортсменов: 8 из Южного ФО, 7 из Центрального ФО, остальные – из Северо-Западный ФО. Порядок, в котором выступают гонщики, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Северо-Западный ФО.
6. Фабрика выпускает шины на автомобиль. В среднем на 100 качественных шин приходится восемь шин со скрытыми дефектами. Найдите вероятность того, что купленная шина окажется качественной. Результат округлите до сотых.
Слайд 25Решения к задачам
1. Общее число элементарных событий N = 4. Событию
благоприятствует только одно
элементарное событие. Поэтому N(A)=1.
Тогда
Ответ: 0,25.
2. Автомобилей всего шесть. Значит, N=6. Событию A={сделают иномарку} благоприятствует два элементарных события: Ford, Chevrolet. Поэтому N(A) = 2. Элементарные события равновозможные. Поэтому
Ответ:
Слайд 263.Элементарный исход в этом опыте – порядочная пара чисел. Первое число
Напишем в каждой клетке таблицы сумму выпавших очков и закрасим клетки где сумма равна 8. Таких ячеек 5. Значит событию А = {сумма равна 8} благоприятствует пять элементарных исходов. Следовательно, N(A) = 5.
Поэтому
Слайд 274. Всего билетов N=4+7+9+5+5=25. Событию А = {билет про ходовую часть}
Тогда
5. Элементарные события – спортсмен, выступающий первым. Поэтому N=20. Чтобы найти число элементарных событий, благоприятствующих событию А = {первым выступит спортсмен из Северо-Западный ФО }, нужно подсчитать число спортсменов из Северо-Западный ФО: N(A)=20-(8+7)=5. Все элементарные события равновозможные по условию задачи, поэтому
6. Элементарный исход – случайно выбранная шина. Поэтому N = 108.
Событию А = {качественная шина} благоприятствуют 100 исходов.
Поэтому N(A) = 100.
Тогда
Слайд 28Итог урока
Домашнее задание:
Придумать 5 задач, связанных с профессией автомеханик, на нахождение
Слайд 291. А.Г.Мордкович. Алгебра и начала математического анализа.
10 - 11классы. В
2. А.Г.Мордкович и др. Алгебра и начала математического анализа.
10 – 11классы. В 2 ч. Ч. 2. Задачник;
3. И.Р.Высоцкий, И.В.Ященко. ЕГЭ 2012. Математика. Задача В10.
Теория вероятностей. Рабочая тетрадь/ Под редакцией А.Л.Семенова,
И.В.Ященко. Москва. Издательство МЦНМО, 2012;
4. Задача В10. Открытый банк заданий по математике. ЕГЭ 2012.
5. Интернет – источники:
http://www.toehelp.ru/theory/ter_ver/1_3/
http://ssau2011.narod2.ru/l1.htm
Литература.