характеристик в курсе школьной математики
Урок математики в 7 классе
Автор: Еланцева Светлана Викторовна,
учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Изучение статистических характеристик в школе
Содержание
- 1. Презентация по математике на тему Изучение статистических характеристик в школе
- 2. Среднее арифметическоеОпределение: Средним
- 3. Пример: Средняя оценка успеваемости
- 4. Мода (Мо) Модой называется то число, которое
- 5. Пример нахождения моды:В отделе мужской обуви универмага
- 6. Наибольшее и наименьшее
- 7. Медиана (Ме)Определение: Медианой набора чисел называют такое
- 8. Примеры нахождения медианыПример 1. Возьмём какой-нибудь набор
- 9. Среднее геометрическоеОпределение. Средним геометрическим нескольких чисел называется
- 10. Слайд 10
- 11. Слайд 11
- 12. Производство картофеля ( ц/га)Среднее арифметическое =
- 13. Упражнения1. Записан вес (в кг) семи учащихся:42,
- 14. Упражнения2. Записан примерный пробег (в тыс.км) шести
- 15. Упражнения 3. Даны числа: 18, 125, и 12.
- 16. Упражнения4. Записан вес (в кг) шести учащихся:
- 17. Упражнения5. В таблице приведены данные о пяти
- 18. Упражнения6. В таблице приведены данные книжного магазина
Среднее арифметическоеОпределение: Средним арифметическим нескольких чисел называется число, равное отношению суммы этих чисел к их количеству.
Слайд 1Муниципальное казенное образовательное учреждение
«Малокрасноярская основная общеобразовательная школа»
Кыштовского района Новосибирской области
Изучение статистических
Слайд 2 Среднее арифметическое
Определение: Средним арифметическим нескольких чисел называется
число, равное отношению суммы этих чисел к их количеству.
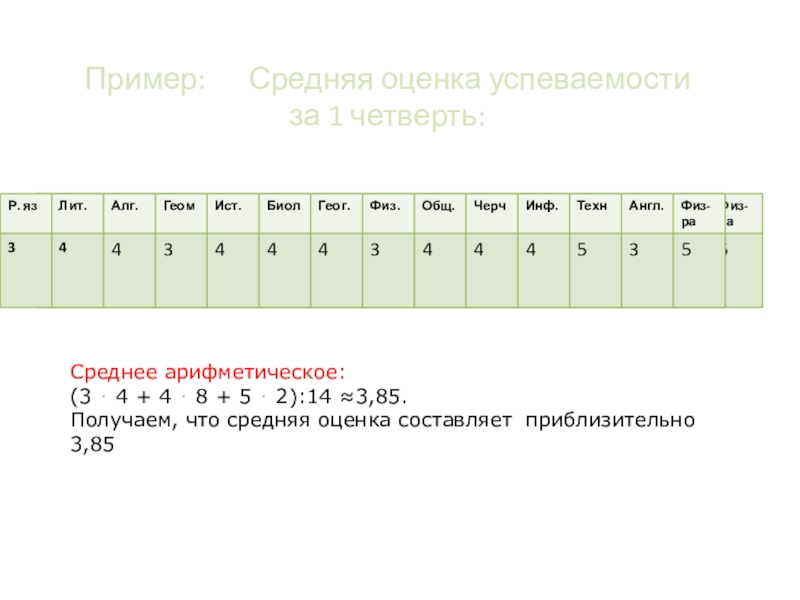
Слайд 3Пример: Средняя оценка успеваемости за 1 четверть:
Среднее арифметическое:
(3
4 + 4 8 + 5 2):14 ≈3,85.
Получаем, что средняя оценка составляет приблизительно 3,85
Получаем, что средняя оценка составляет приблизительно 3,85
Слайд 4Мода (Мо)
Модой называется то число, которое в данном числовом ряду
встречается чаще всего. В числовом ряду может быть одна мода или несколько.
Например: Найти моду ряда чисел: 2,2,3,3,3,4,4,5,5,5,5,6,6,7. Чаще всего встречается число 5, значит Мо = 5.
Например: Найти моду ряда чисел: 2,2,3,3,3,4,4,5,5,5,5,6,6,7. Чаще всего встречается число 5, значит Мо = 5.
Слайд 5Пример нахождения моды:
В отделе мужской обуви универмага в течение дня производился
учет размеров купленной обуви.
Были получены следующие результаты: 42, 40, 43, 39, 42, 42, 45, 41, 43, 43, 41, 42, 46, 40, 42, 42, 39, 42, 45, 42, 43, 42, 44, 41, 42.
Какой размер обуви наиболее распространен, т.е. найти моду.
Чаще всего встречается 42 размер, значит Мо = 42
Были получены следующие результаты: 42, 40, 43, 39, 42, 42, 45, 41, 43, 43, 41, 42, 46, 40, 42, 42, 39, 42, 45, 42, 43, 42, 44, 41, 42.
Какой размер обуви наиболее распространен, т.е. найти моду.
Чаще всего встречается 42 размер, значит Мо = 42
Слайд 6 Наибольшее и наименьшее
значение. Размах (А).
Определение: Разность между наибольшим и наименьшим числом называется размахом набора чисел.
Урожай картофеля в сёлах А и В:
Самый большой урожай в селе А:180ц/га, самый маленький - 50 ц/га.
В селе В: самый большой – 130 ц/га, самый маленький – 100 ц/га. Размах производства картофеля в селе А: 180 – 50 = 130,
в селе В: 130 – 100 = 30.
Слайд 7Медиана (Ме)
Определение: Медианой набора чисел называют такое число, которое разделяет набор
на две равные по численности части.
Прежде чем искать медиану ряда, нужно упорядочить ряд чисел.
Прежде чем искать медиану ряда, нужно упорядочить ряд чисел.
Слайд 8Примеры нахождения медианы
Пример 1. Возьмём какой-нибудь набор различных чисел, например 1,4,7,9,11
- чётный ряд
Медианой в этом случае оказывается число, стоящее в точности посередине, m=7.
Пример 2. Рассмотрим набор 1,3,6,11. – нечётный ряд Медианой этого набора служит число, равное полусумме чисел, стоящих посередине:
(3+6):2=4,5
Медианой этого набора считают число 4,5.
Медианой в этом случае оказывается число, стоящее в точности посередине, m=7.
Пример 2. Рассмотрим набор 1,3,6,11. – нечётный ряд Медианой этого набора служит число, равное полусумме чисел, стоящих посередине:
(3+6):2=4,5
Медианой этого набора считают число 4,5.
Слайд 9Среднее геометрическое
Определение. Средним геометрическим нескольких чисел называется квадратный корень из произведения
этих чисел.
Например: Даны числа: 2; 5; 10.
Ср. геометрическое = 2*5*10 =10
Например: Даны числа: 2; 5; 10.
Ср. геометрическое = 2*5*10 =10
Слайд 10 Отклонения
Определение: отклонение –
это разница между каждым числом набора и средним арифметическим ряда чисел.
Пример:
Возьмём набор чисел 1,6,7,9,12.
Вычислим среднее арифметическое: (1+6+7+9+12):5=7. Найдём отклонение каждого числа от среднего арифметического:
1-7=-6, 6-7=-1, 7-7=0, 9-7=2, 12-7=5.
Сумма отклонений чисел от среднего арифметического этих чисел равна нулю.
Пример:
Возьмём набор чисел 1,6,7,9,12.
Вычислим среднее арифметическое: (1+6+7+9+12):5=7. Найдём отклонение каждого числа от среднего арифметического:
1-7=-6, 6-7=-1, 7-7=0, 9-7=2, 12-7=5.
Сумма отклонений чисел от среднего арифметического этих чисел равна нулю.
Слайд 11 Дисперсия
Определение: среднее
арифметическое квадратов отклонений от среднего значения называется в статистике дисперсией набора чисел.
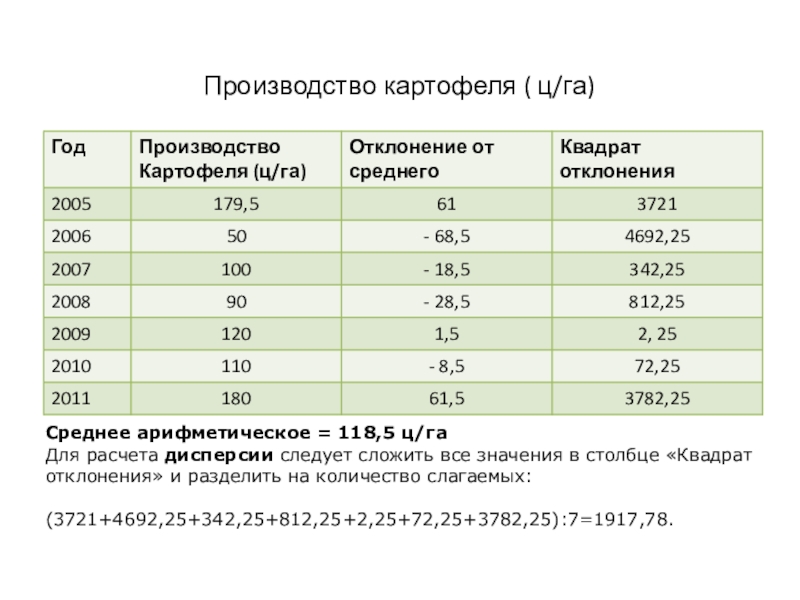
Слайд 12 Производство картофеля ( ц/га)
Среднее арифметическое = 118,5 ц/га
Для расчета дисперсии
следует сложить все значения в столбце «Квадрат отклонения» и разделить на количество слагаемых:
(3721+4692,25+342,25+812,25+2,25+72,25+3782,25):7=1917,78.
(3721+4692,25+342,25+812,25+2,25+72,25+3782,25):7=1917,78.
Слайд 13Упражнения
1. Записан вес (в кг) семи учащихся:
42, 59, 48, 52, 61,
45, 64. Насколько среднее арифметическое этого набора чисел больше его медианы?
Решение. Упорядочим ряд чисел:
42,45,48, 52, 59, 61, 64.
Среднее арифметическое: (42+45+48+52+59+61+64):7=53
Медиана: 52
Разница: 53 - 52 = 1
Решение. Упорядочим ряд чисел:
42,45,48, 52, 59, 61, 64.
Среднее арифметическое: (42+45+48+52+59+61+64):7=53
Медиана: 52
Разница: 53 - 52 = 1
Слайд 14Упражнения
2. Записан примерный пробег (в тыс.км) шести автомобилей: 70, 127, 70,
60, 53, 70. Насколько отличается мода этого набора чисел от его среднего арифметического?
Решение.
Среднее арифметическое ряда:
( 70 + 127 + 70 + 60 + 53 + 70) : 6 = 75
Мода: 70
Разница: 75 – 70 = 5
Решение.
Среднее арифметическое ряда:
( 70 + 127 + 70 + 60 + 53 + 70) : 6 = 75
Мода: 70
Разница: 75 – 70 = 5
Слайд 15Упражнения
3. Даны числа: 18, 125, и 12. Найти разность между средним
арифметическим и средним геометрическим этих чисел.
Решение.
Среднее арифметическое:
(18 + 125 + 12) : 3 = 51,6
Среднее геометрическое:
18 125 12 = 164,3
Разность: 164,3 – 51,6 = 112,7
Решение.
Среднее арифметическое:
(18 + 125 + 12) : 3 = 51,6
Среднее геометрическое:
18 125 12 = 164,3
Разность: 164,3 – 51,6 = 112,7
Слайд 16Упражнения
4. Записан вес (в кг) шести учащихся:
55, 54, 61, 58,
55, 59. Насколько максимальное значение этого набора чисел отличается от его среднего арифметического?
Решение: Максимальное значение = 61
Среднее арифметическое = (55+54+61+58+55+59) : 6 = 57
Разница: 61 – 57 = 4
Решение: Максимальное значение = 61
Среднее арифметическое = (55+54+61+58+55+59) : 6 = 57
Разница: 61 – 57 = 4
Слайд 17Упражнения
5. В таблице приведены данные о пяти лучших результатах прыжков в
длину с места учащихся старших классов:
Определить дисперсию результатов прыжков, представленных в таблице. (Ответ округлить до сотых).
Решение. Среднее арифметическое:(183+185+180+186+185):5=183,8
Отклонения:(- 0,8; 1,2; - 3,8; 2,2; 1,2) (Проверка: Сумма = 0)
Квадрат отклонений: 0,64; 1,44; 14,44, 4,84; 1,44.
Дисперсия = (0,64 + 1,44 + 14,44 + 4,84 + 1,44) : 5 = 4,56.
Определить дисперсию результатов прыжков, представленных в таблице. (Ответ округлить до сотых).
Решение. Среднее арифметическое:(183+185+180+186+185):5=183,8
Отклонения:(- 0,8; 1,2; - 3,8; 2,2; 1,2) (Проверка: Сумма = 0)
Квадрат отклонений: 0,64; 1,44; 14,44, 4,84; 1,44.
Дисперсия = (0,64 + 1,44 + 14,44 + 4,84 + 1,44) : 5 = 4,56.
Слайд 18Упражнения
6. В таблице приведены данные книжного магазина о количестве проданных книг
шести авторов в течение месяца:
Определить, насколько отличается размах от медианы ряда количества проданных книг этих авторов.
Решение.
Упорядочим ряд: 30, 35, 38, 40, 42, 45. Размах = (45 – 30) = 15
Медиана = (38 + 40) : 2 = 36.
Разница: 36 – 15 = 21
Определить, насколько отличается размах от медианы ряда количества проданных книг этих авторов.
Решение.
Упорядочим ряд: 30, 35, 38, 40, 42, 45. Размах = (45 – 30) = 15
Медиана = (38 + 40) : 2 = 36.
Разница: 36 – 15 = 21