- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Измерение величин(5 класс)
Содержание
- 1. Презентация по математике на тему Измерение величин(5 класс)
- 2. Темы уроков Прямая. Луч. Отрезок.Измерение отрезков. Метрические единицы длины.Окружность и круг. Сфера и шар.Углы. Измерение углов.Треугольники.Четырехугольники.
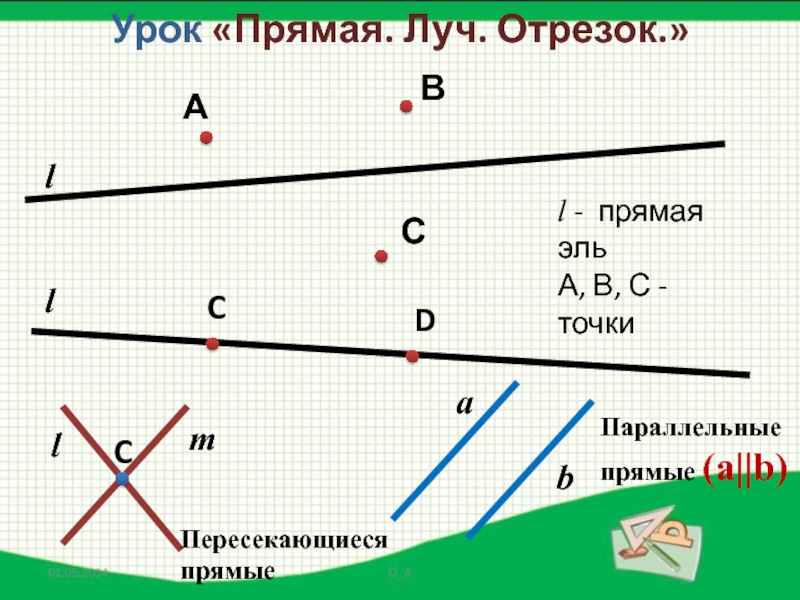
- 3. Урок «Прямая. Луч. Отрезок.»АВСll - прямая эльА, В, С - точкиПересекающиеся прямые
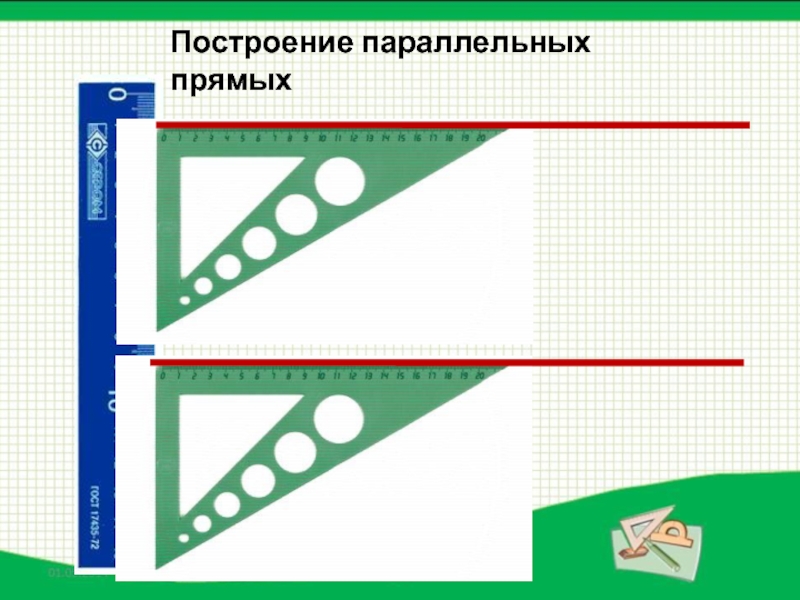
- 4. Построение параллельных прямых
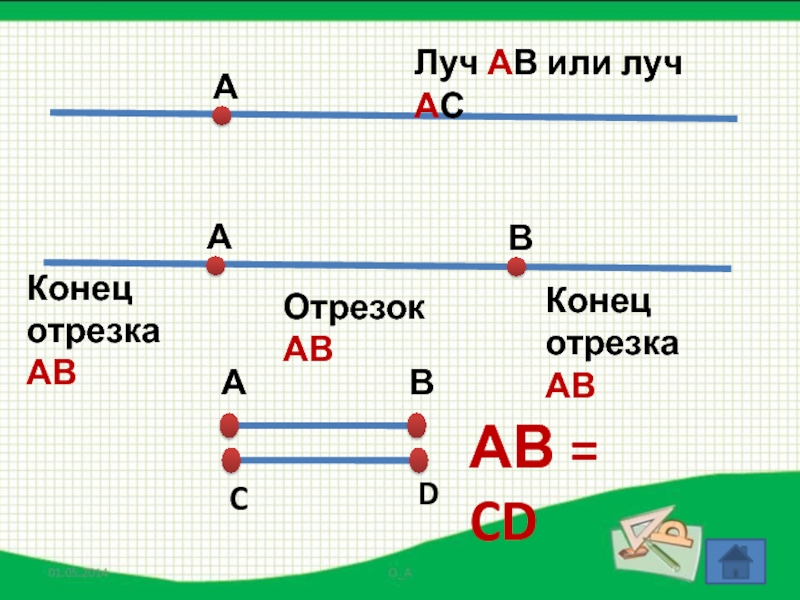
- 5. АЛуч АВ или луч АСАОтрезок АВВКонец отрезка АВКонец отрезка АВАВ = CD
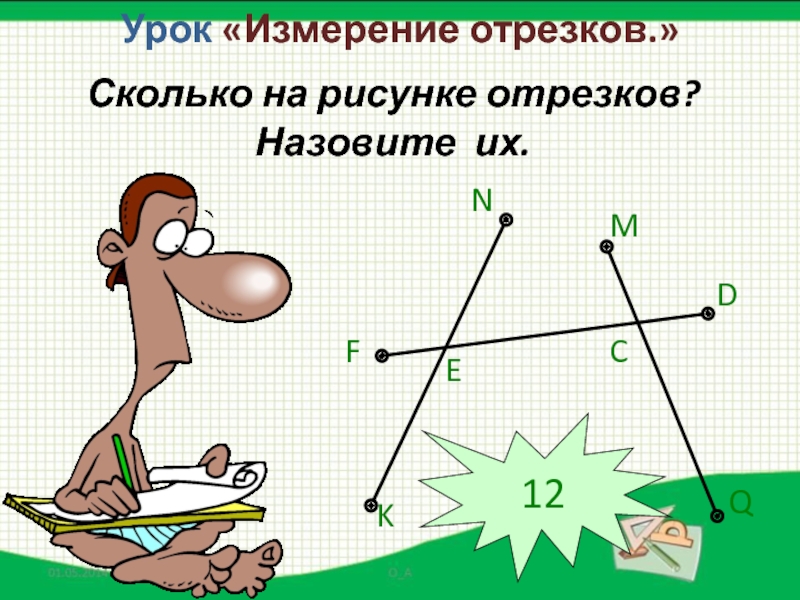
- 6. Сколько на рисунке отрезков? Назовите их.NKFDEMQC12Урок «Измерение отрезков.»
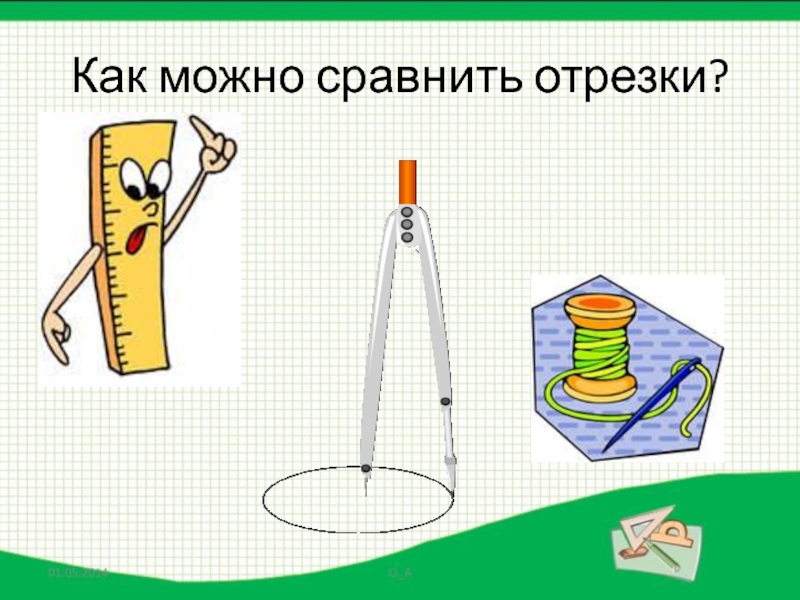
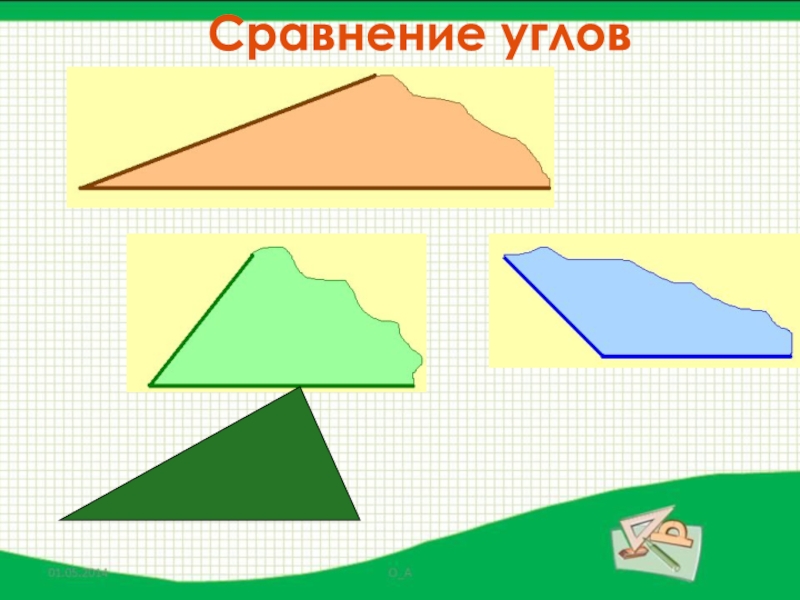
- 7. Как можно сравнить отрезки?
- 8. 1см 1мм 1км 1дм 1 мКакие
- 9. Решение задач на нахождение длин отрезков.А) АС=3см, СВ=5см, АВ=?Б) АВ=10см, АС=4см, СВ=?В) АВ=12 см, АС=СВ, АС=?
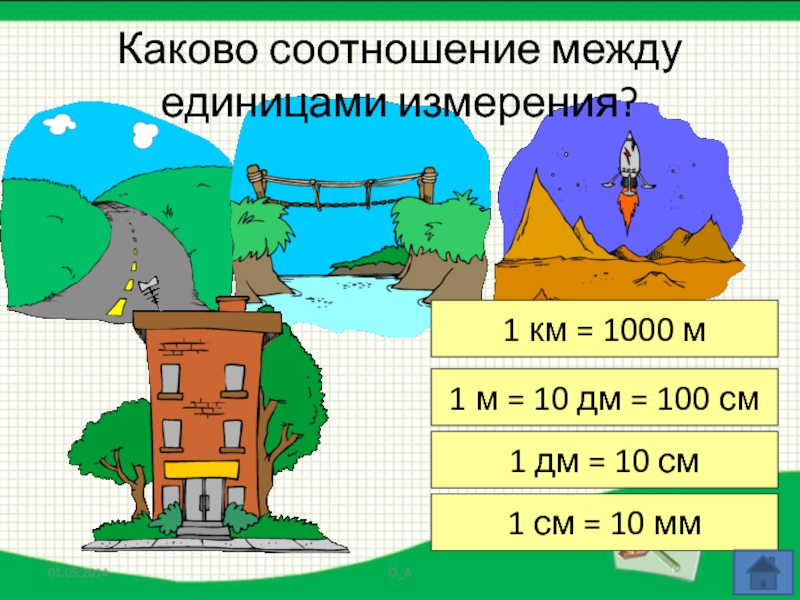
- 10. 1 км = 1000 м1 м =
- 11. Тема: Окружность и круг
- 12. Слайд 12
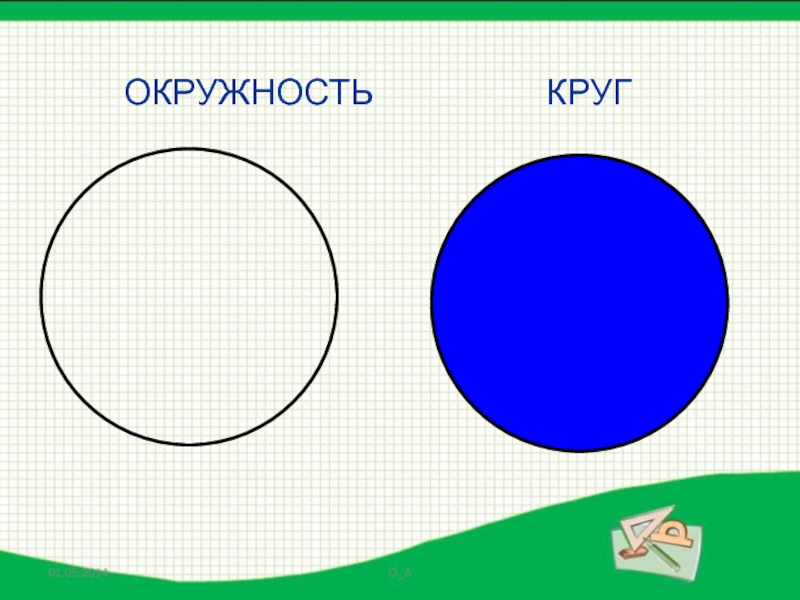
- 13. КРУГОКРУЖНОСТЬ
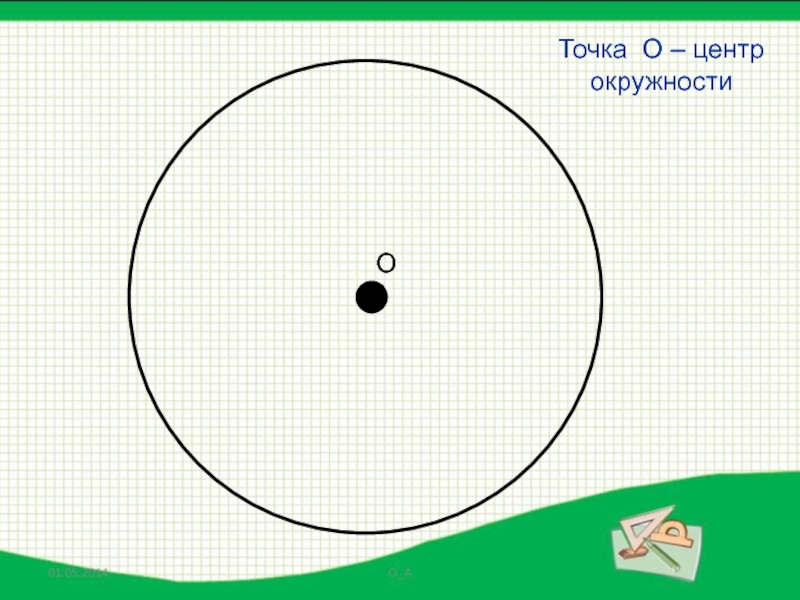
- 14. ОТочка О – центр окружности
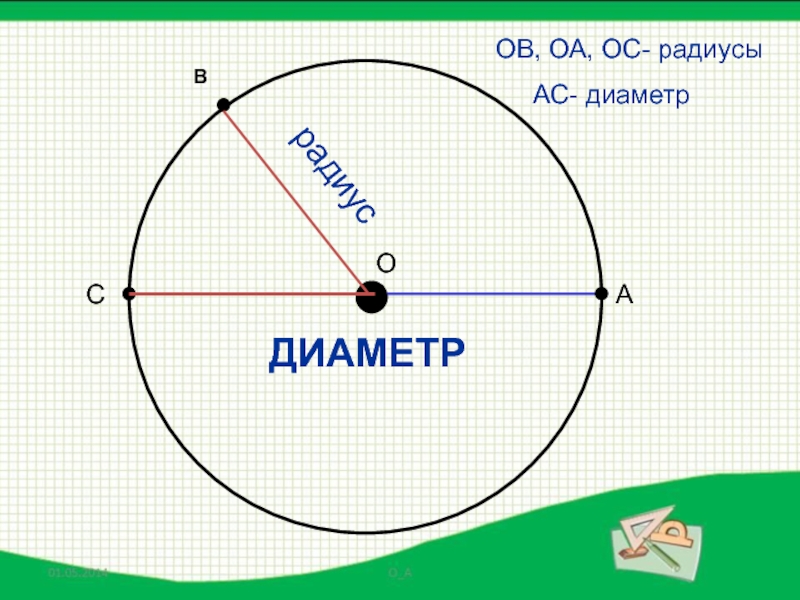
- 15. ОАОВ, ОА, ОС- радиусы АС- диаметррадиусСВДИАМЕТР
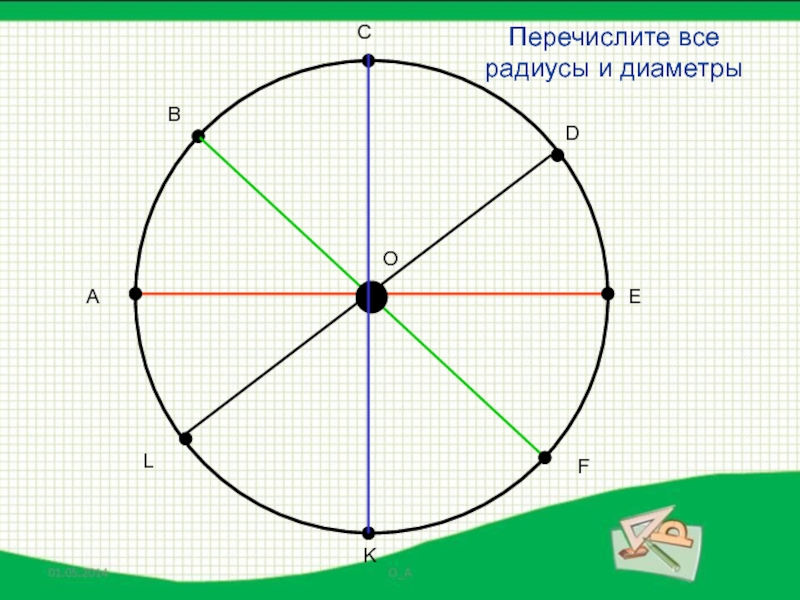
- 16. АВСDEFKLOПеречислите все радиусы и диаметры
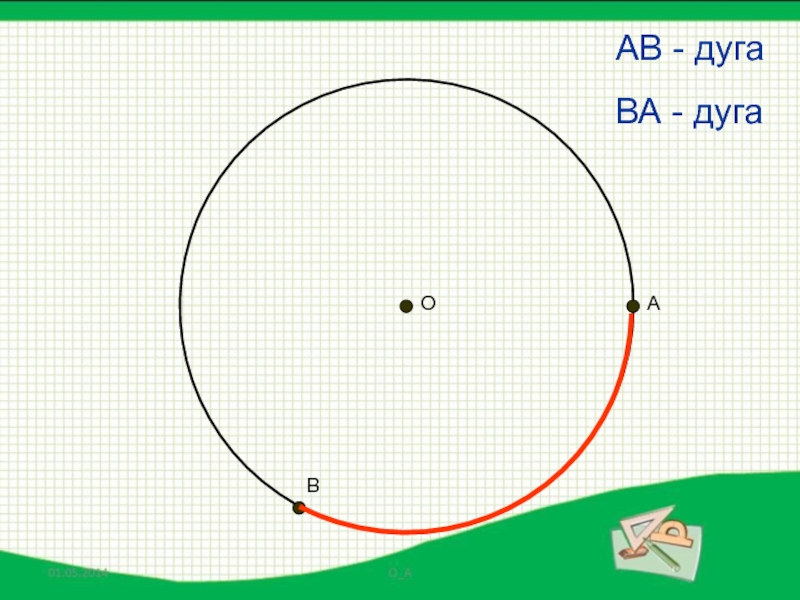
- 17. АВ - дугаАВОВА - дуга
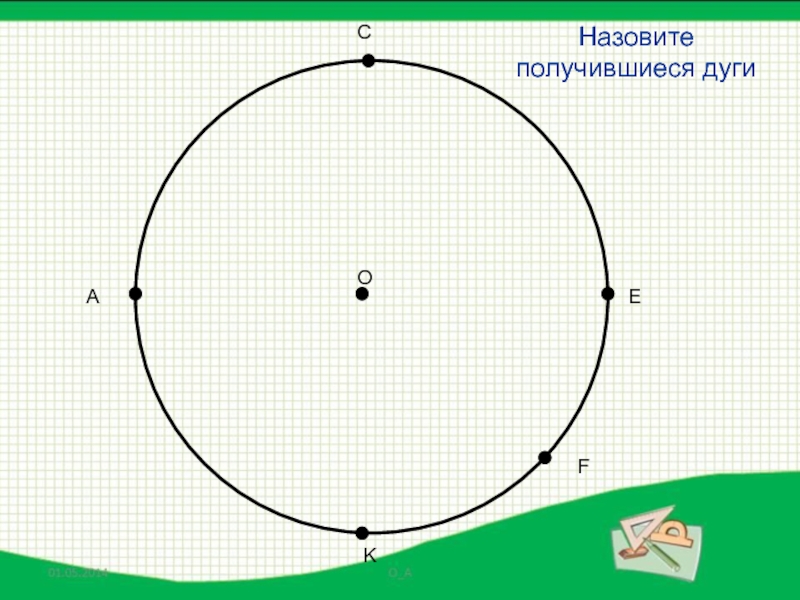
- 18. АСEFKOНазовите получившиеся дуги
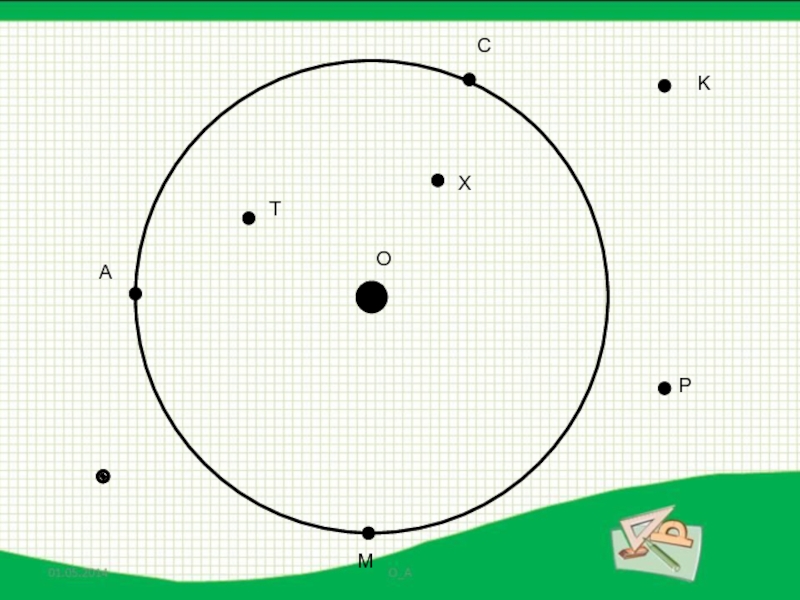
- 19. ОАСMPKTX
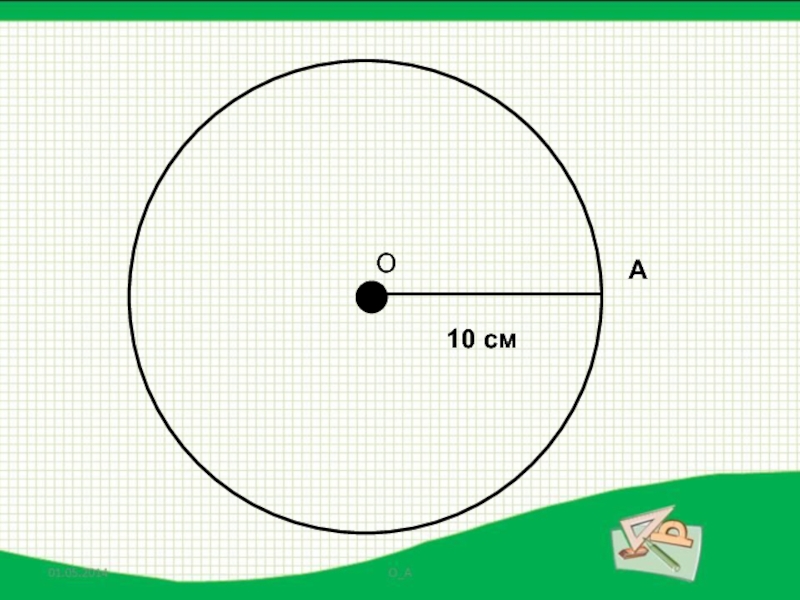
- 20. ОА10 см
- 21. Слайд 21
- 22. Дополните предложение:Окружность и круг - ….У окружности и круга есть - …Радиус – это….Диаметр равен…
- 23. Построение и измерение углов
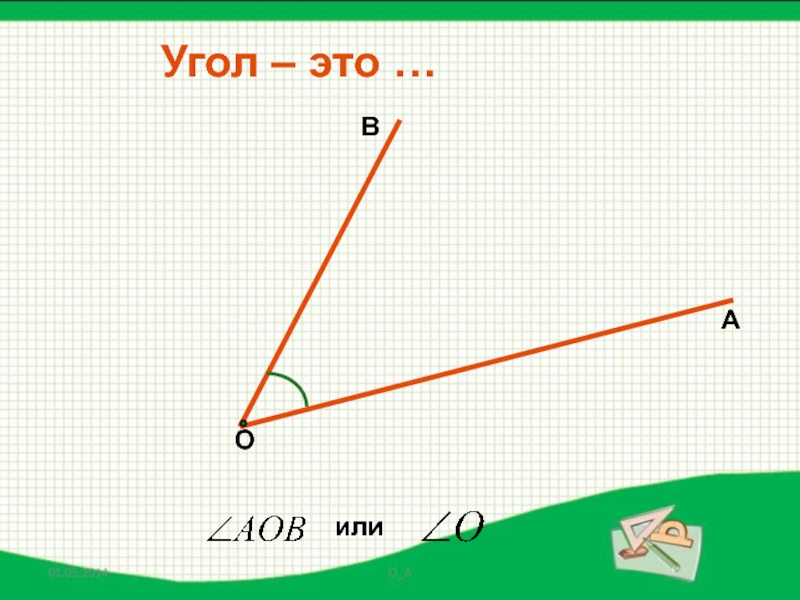
- 24. Угол – это …или
- 25. Сравнение углов
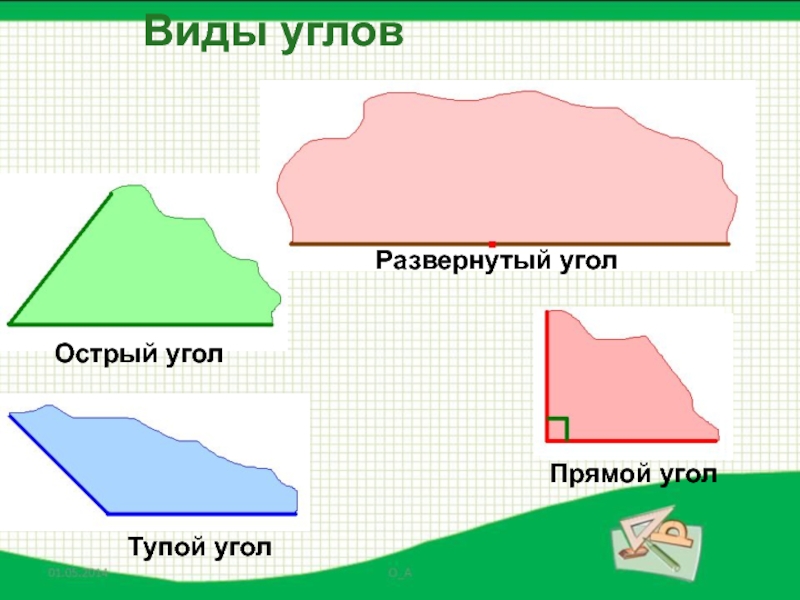
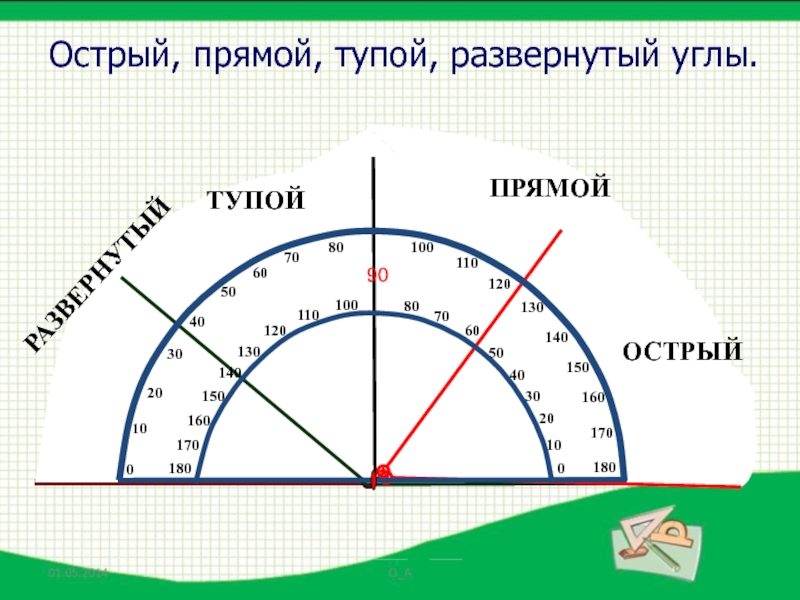
- 26. Виды угловОстрый уголТупой уголПрямой уголРазвернутый угол
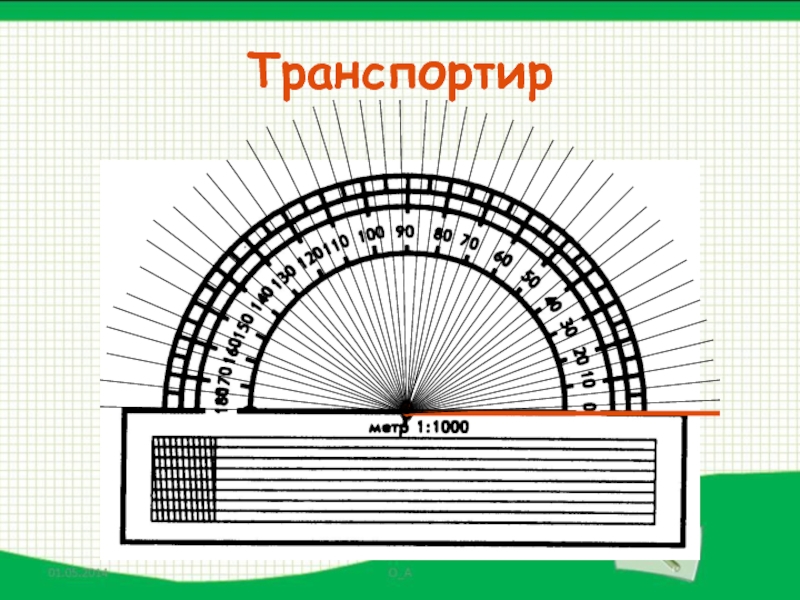
- 27. Транспортир
- 28. Слайд 28
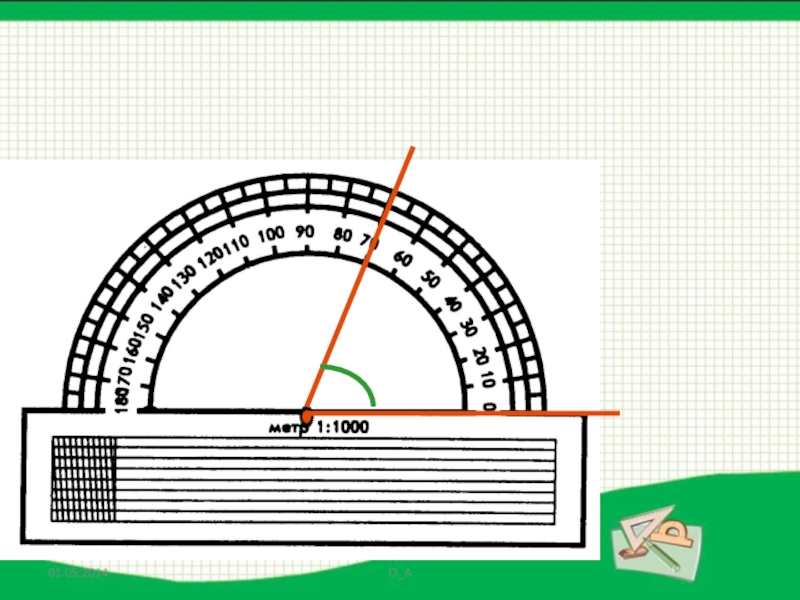
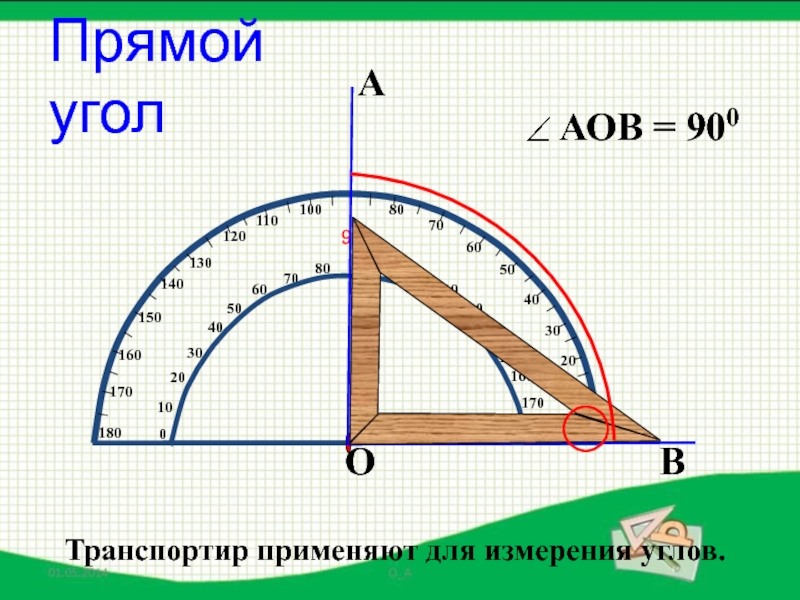
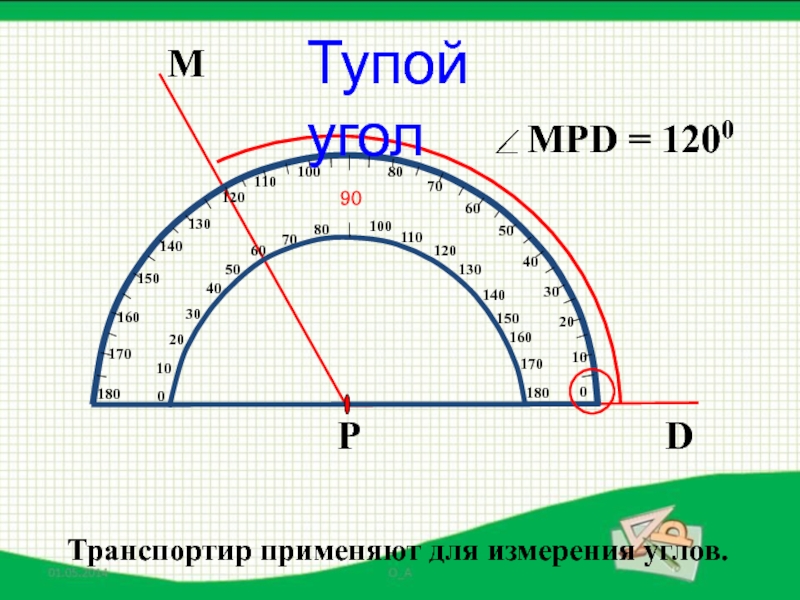
- 29. АВОПрямой уголТранспортир применяют для измерения углов.
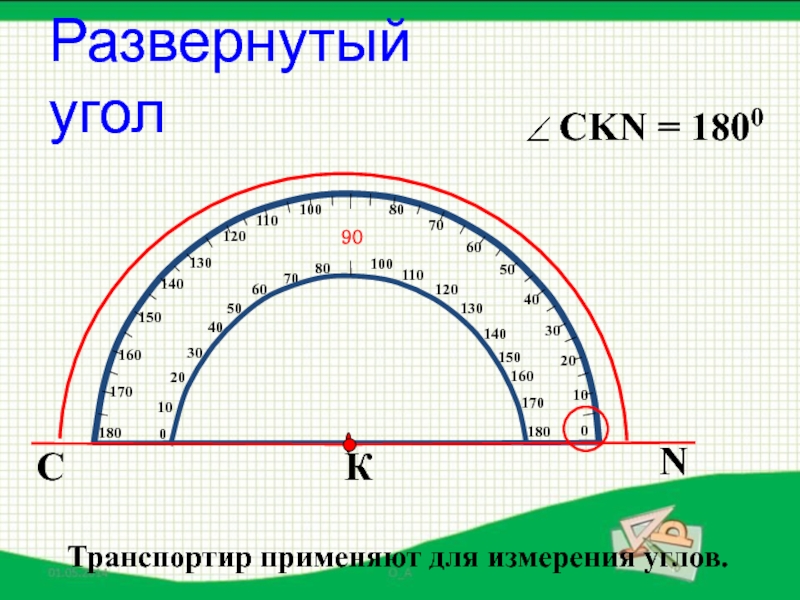
- 30. СNКРазвернутый уголТранспортир применяют для измерения углов.
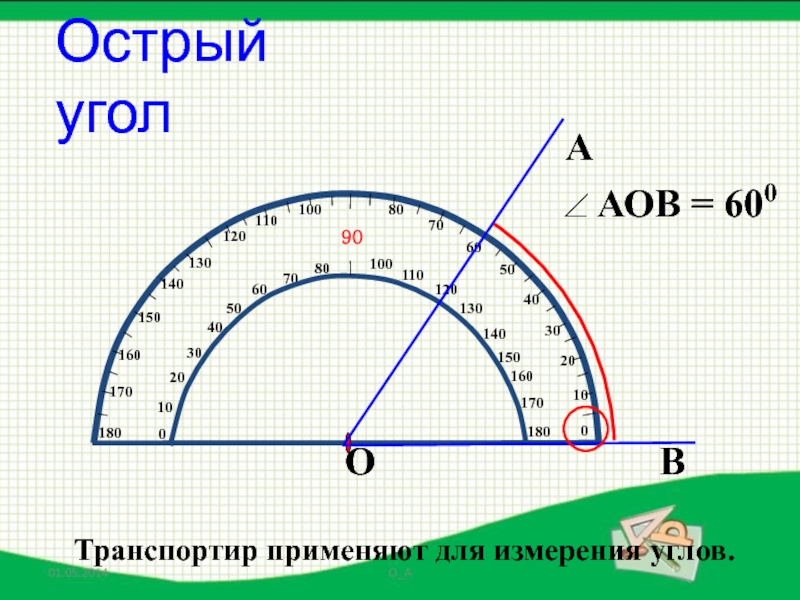
- 31. Острый уголТранспортир применяют для измерения углов.
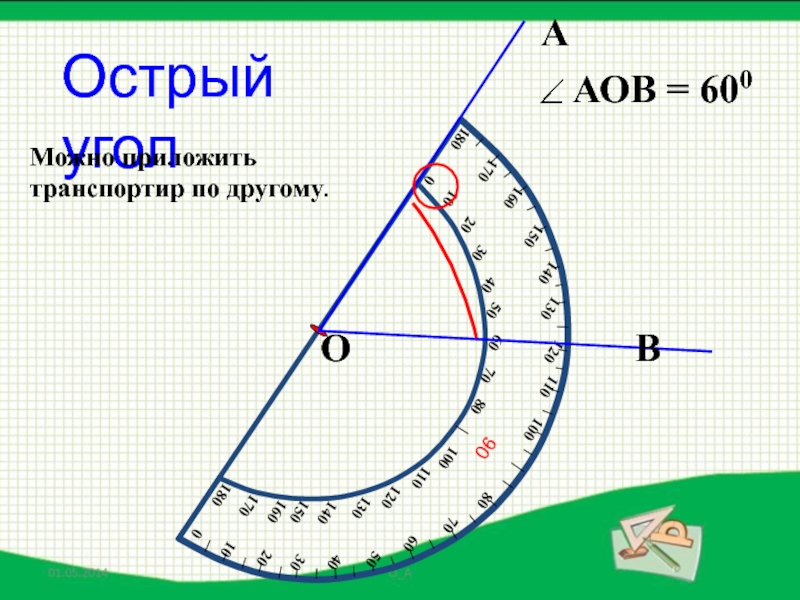
- 32. АВООстрый уголМожно приложить транспортир по другому.
- 33. Тупой уголТранспортир применяют для измерения углов.
- 34. Острый, прямой, тупой, развернутый углы.
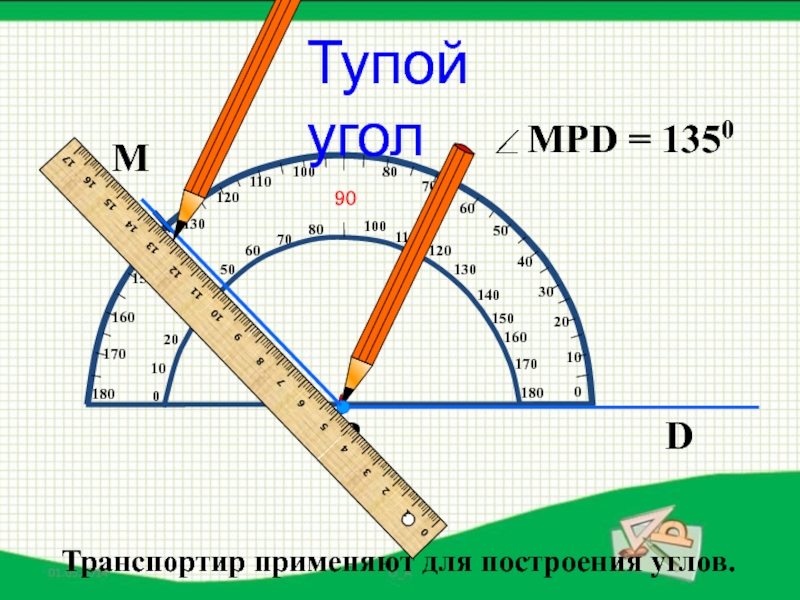
- 35. МТупой уголТранспортир применяют для построения углов.
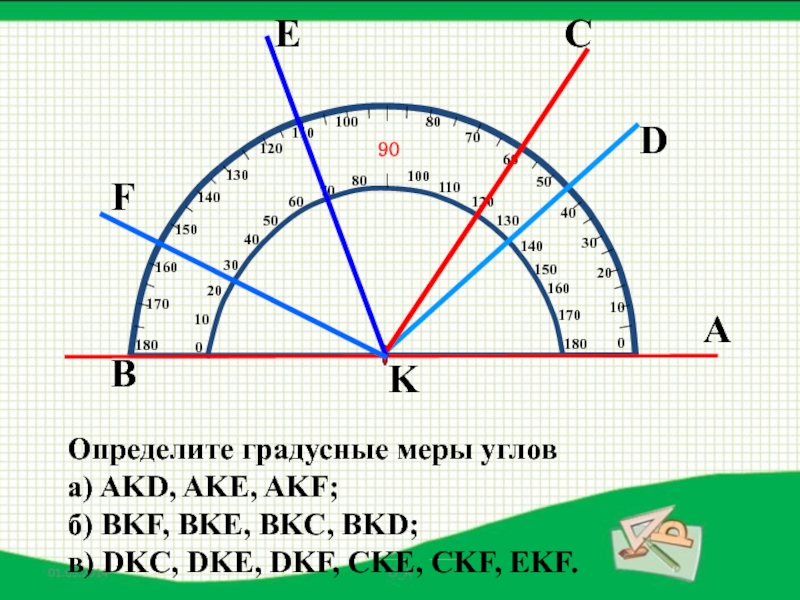
- 36. АKBFECDОпределите градусные меры углов a) AKD, AKE,
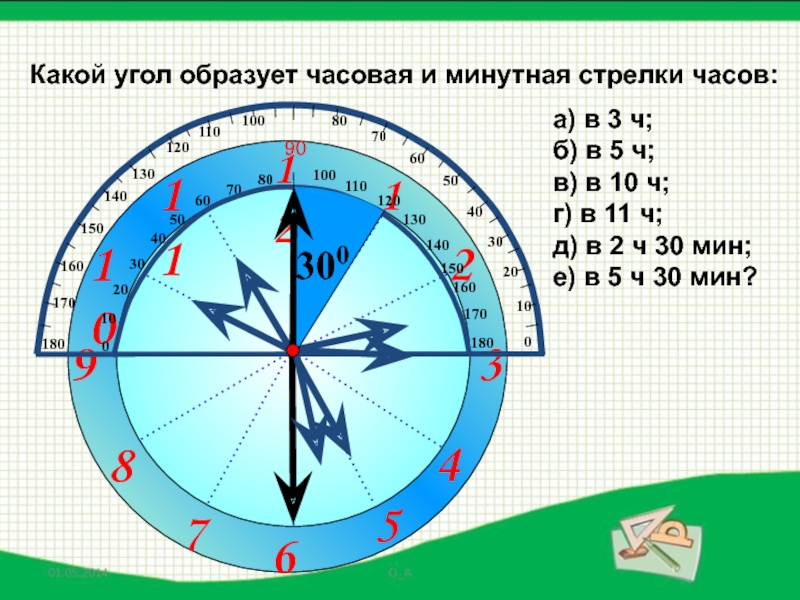
- 37. 123961211108745Какой угол образует часовая и минутная стрелки
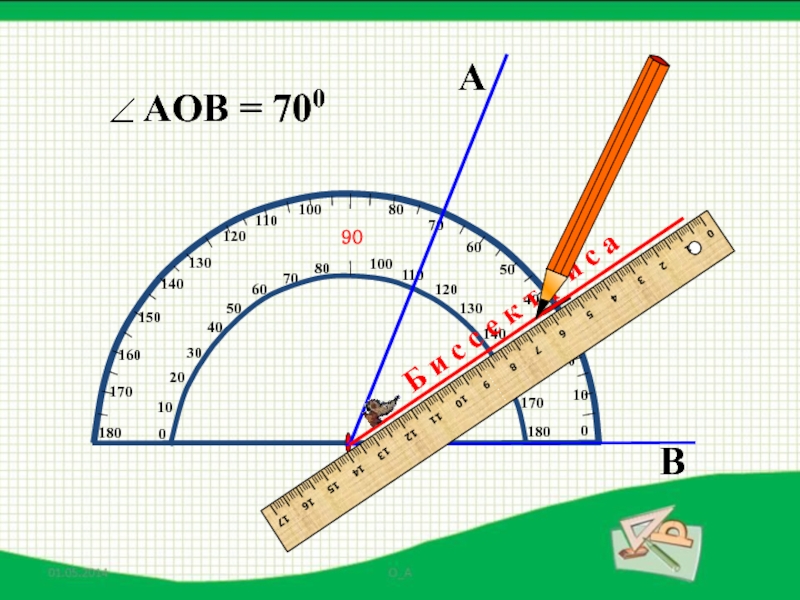
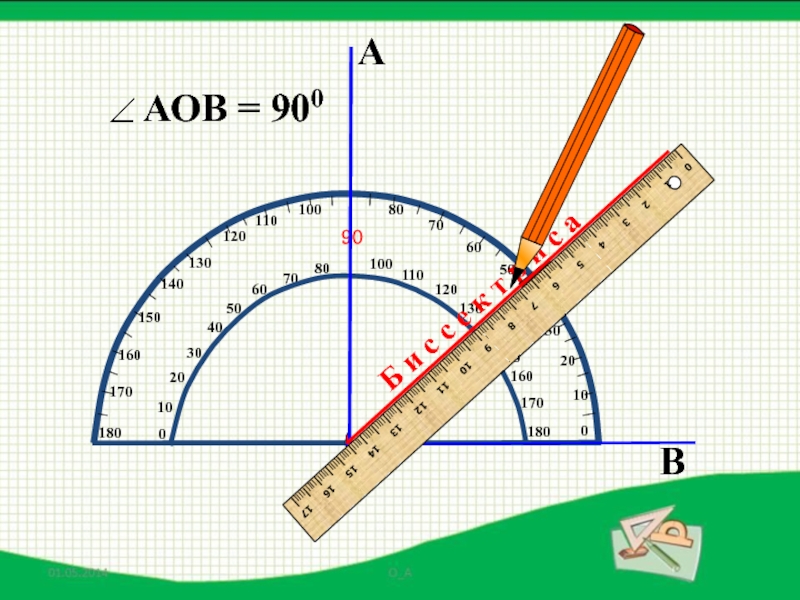
- 38. АВОБ и с с е к т р и с а
- 39. АВОБ и с с е к т р и с а
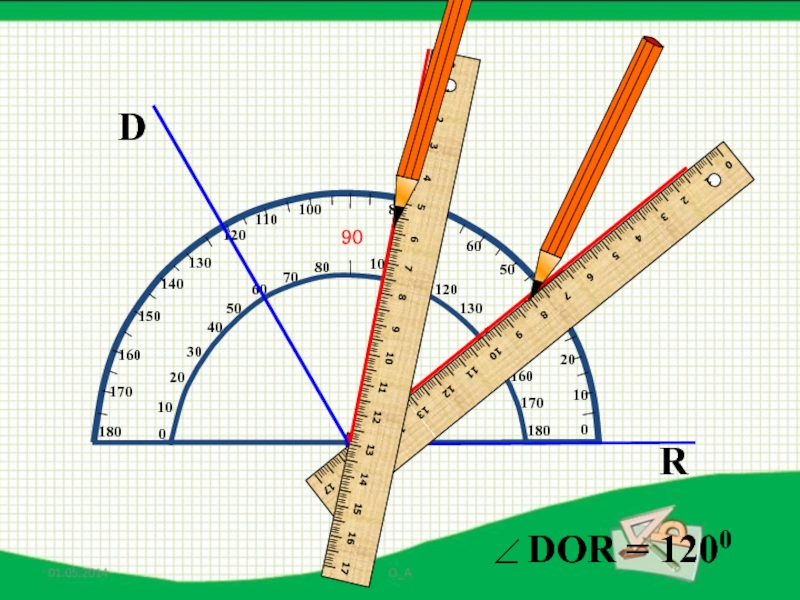
- 40. DRО
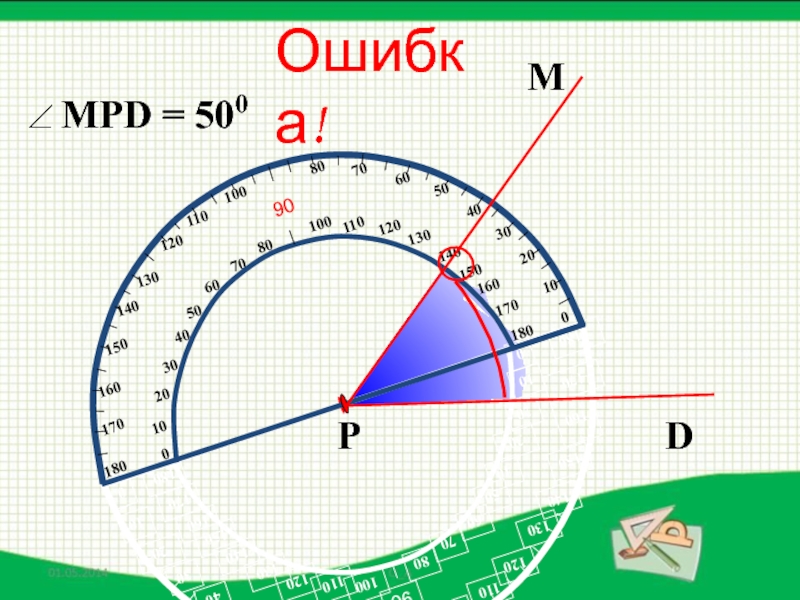
- 41. Ошибка!
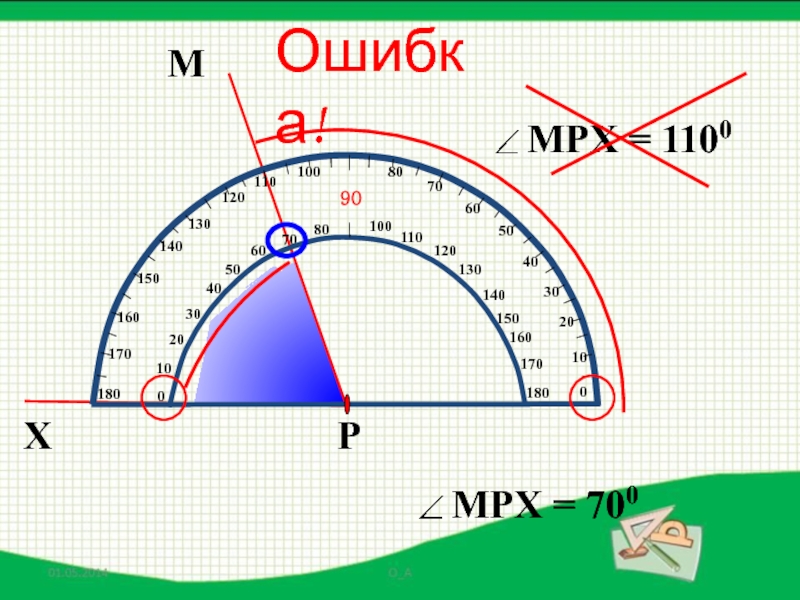
- 42. МXРОшибка!
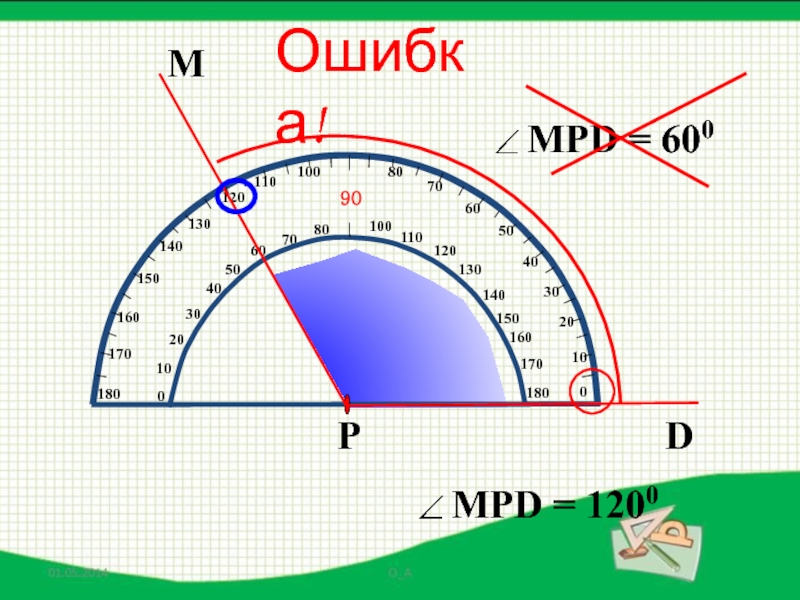
- 43. МDРОшибка!
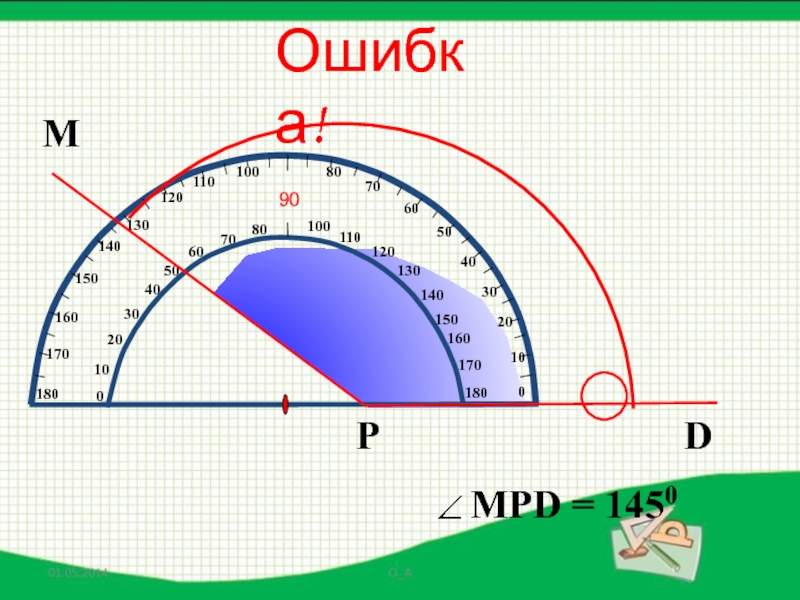
- 44. МDРОшибка!
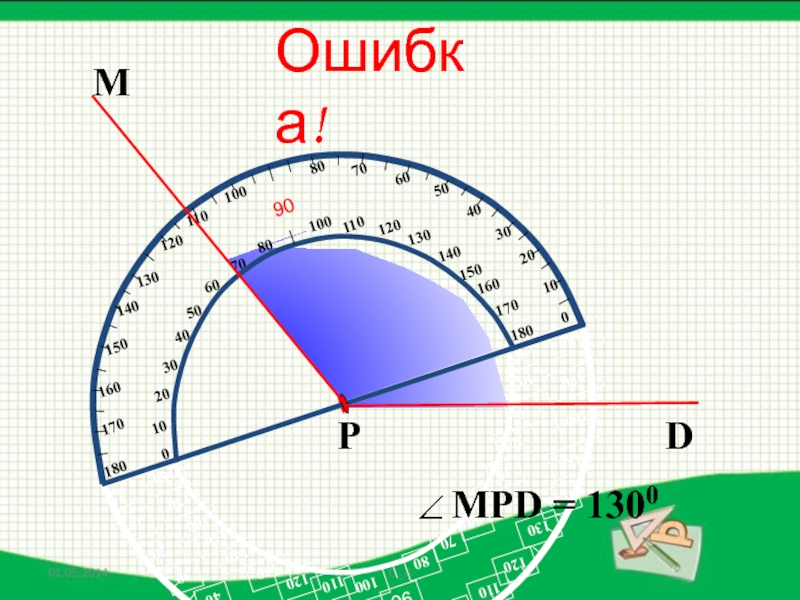
- 45. МDРОшибка!
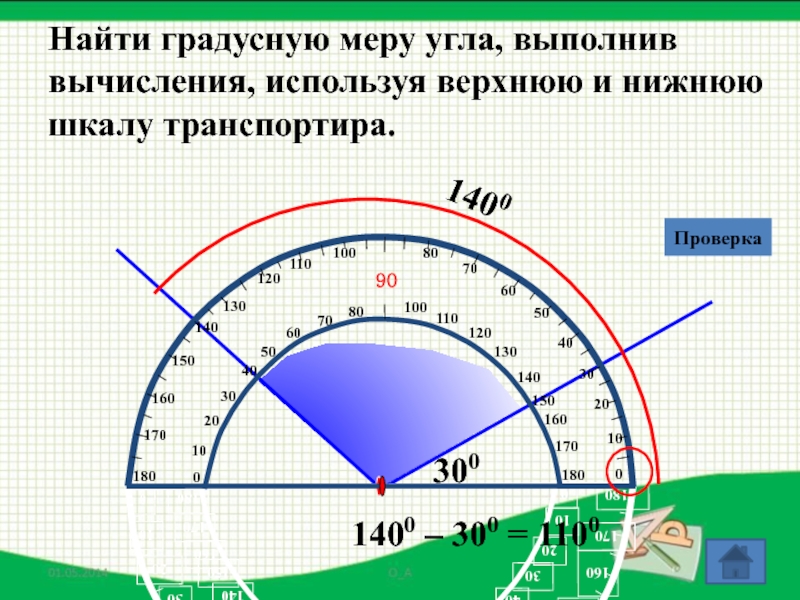
- 46. Найти градусную меру угла, выполнив вычисления, используя
- 47. Тема: «Треугольники и их виды»
- 48. Многоугольники:
- 49. Слайд 49
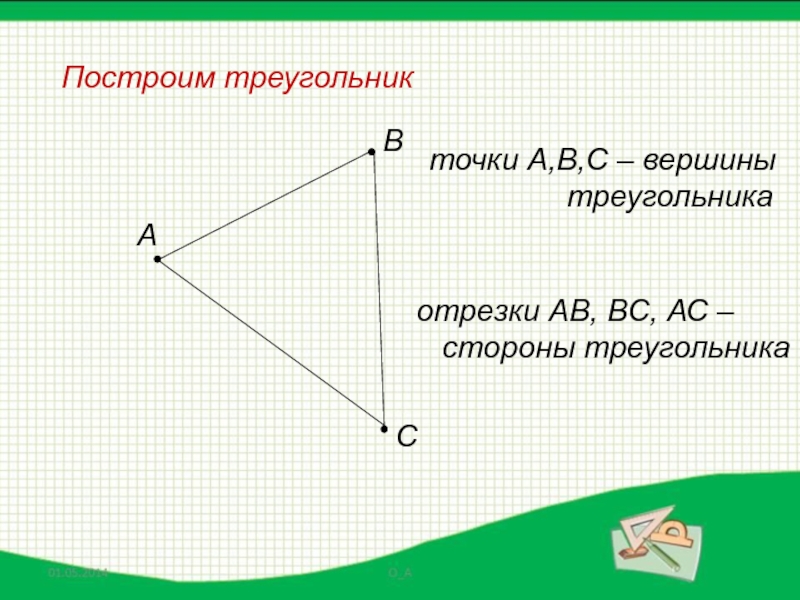
- 50. Построим треугольникАВС точки А,В,С – вершины
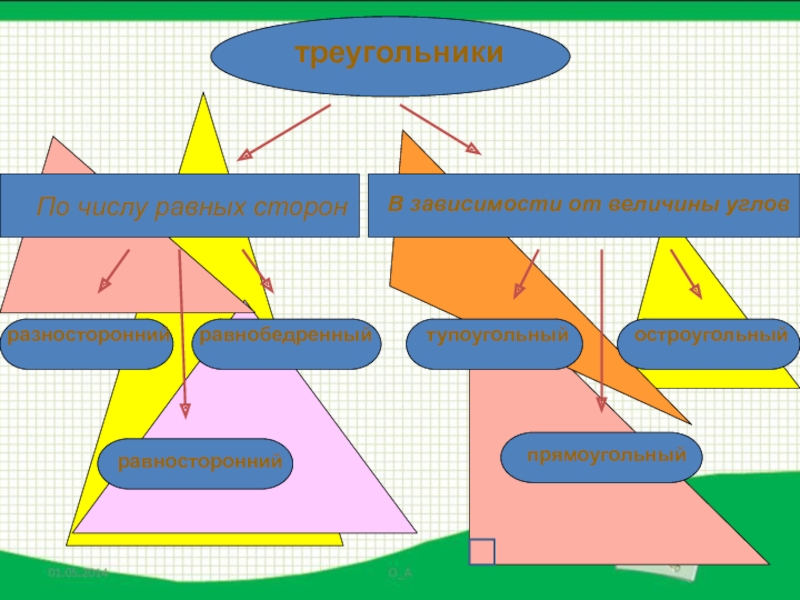
- 51. треугольникиПо числу равных сторонВ зависимости от величины угловразностороннийравнобедренныйравностороннийтупоугольныйостроугольныйпрямоугольный
- 52. Слайд 52
- 53. Первое свойство треугольника:«Сумма двух сторон треугольника всегда
- 54. Чему равна сумма углов в треугольнике?«Оторвите» углы
- 55. Второе свойство треугольника:«Сумма углов любого треугольника равна 180˚»
- 56. Равнобедренный треугольник.основание боковая сторона боковая сторонаАВС
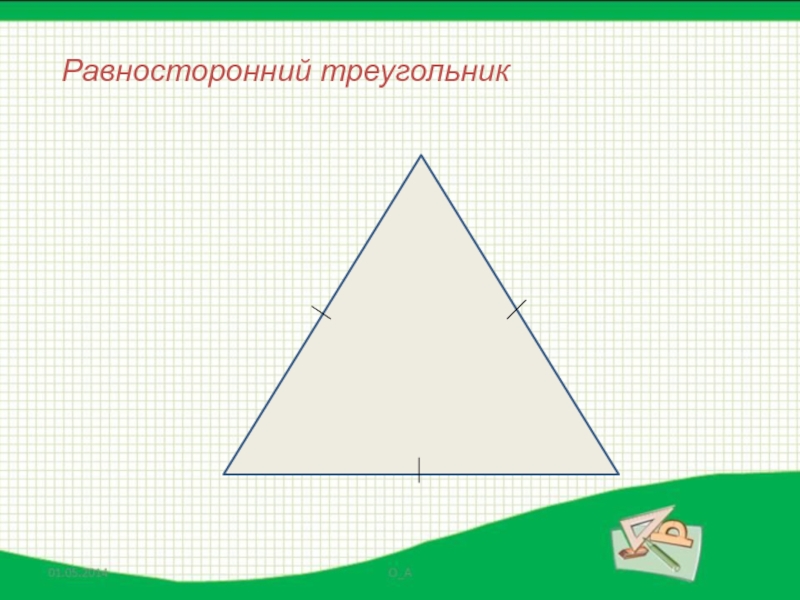
- 57. Равносторонний треугольник
- 58. Ответь на вопросы:1 Можно ли быть уверенным,
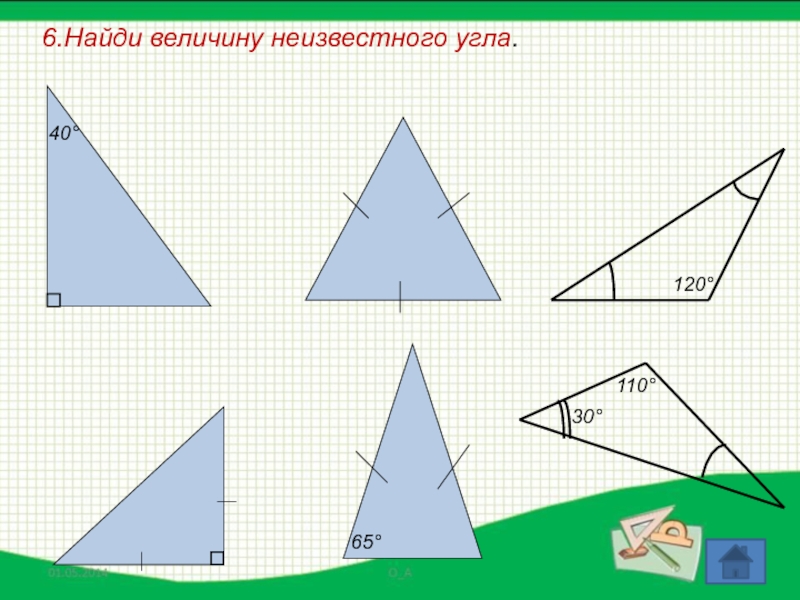
- 59. 6.Найди величину неизвестного угла.40°120°65°110°30°
- 60. Четырехугольники (урок с элементами конструирования)
- 61. Прямоугольник- это параллелограмм, у
- 62. Задание №1: собери прямоугольник из других геометрических фигур.
- 63. Квадрат
- 64. Задание №2: собери квадрат из других геометрических фигур.
- 65. Параллелограмм
- 66. Задание №3: собери параллелограмм из других геометрических фигур.
- 67. Ромб - это
- 68. Задание №4: собери ромб из других геометрических фигур.
- 69. Трапеция
- 70. Слайд 70
- 71. Задание №5: собери трапецию из других геометрических фигур.
Темы уроков Прямая. Луч. Отрезок.Измерение отрезков. Метрические единицы длины.Окружность и круг. Сфера и шар.Углы. Измерение углов.Треугольники.Четырехугольники.
Слайд 2Темы уроков
Прямая. Луч. Отрезок.
Измерение отрезков. Метрические единицы длины.
Окружность и круг.
Сфера и шар.
Углы. Измерение углов.
Треугольники.
Четырехугольники.
Углы. Измерение углов.
Треугольники.
Четырехугольники.
Слайд 8 1см
1мм
1км
1дм
1 м
Какие единицы длины используют при
измерении длин отрезков?
Какая из единиц измерения является основной?
Слайд 9Решение задач на нахождение длин отрезков.
А) АС=3см, СВ=5см, АВ=?
Б) АВ=10см, АС=4см,
СВ=?
В) АВ=12 см, АС=СВ, АС=?
В) АВ=12 см, АС=СВ, АС=?
Слайд 101 км = 1000 м
1 м = 10 дм = 100
см
1 дм = 10 см
1 см = 10 мм
Каково соотношение между единицами измерения?
Слайд 22Дополните предложение:
Окружность и круг - ….
У окружности и круга есть -
…
Радиус – это….
Диаметр равен…
Радиус – это….
Диаметр равен…
Слайд 36А
K
B
F
E
C
D
Определите градусные меры углов
a) AKD, AKE, AKF;
б) BKF, BKE, BKC,
BKD;
в) DKC, DKE, DKF, CKE, CKF, EKF.
в) DKC, DKE, DKF, CKE, CKF, EKF.
Слайд 371
2
3
9
6
12
11
10
8
7
4
5
Какой угол образует часовая и минутная стрелки часов:
300
а) в 3
ч;
б) в 5 ч;
в) в 10 ч;
г) в 11 ч;
д) в 2 ч 30 мин;
е) в 5 ч 30 мин?
б) в 5 ч;
в) в 10 ч;
г) в 11 ч;
д) в 2 ч 30 мин;
е) в 5 ч 30 мин?
Слайд 46Найти градусную меру угла, выполнив
вычисления, используя верхнюю и нижнюю
шкалу
транспортира.
1400
300
Проверка
1400 – 300 = 1100
Слайд 50Построим треугольник
А
В
С
точки А,В,С – вершины
треугольника
отрезки АВ, ВС, АС –
стороны треугольника
Слайд 51треугольники
По числу равных сторон
В зависимости от величины углов
разносторонний
равнобедренный
равносторонний
тупоугольный
остроугольный
прямоугольный
Слайд 53Первое свойство треугольника:
«Сумма двух сторон треугольника
всегда больше третьей стороны»
4
6
7
4
6+7
6 < 4+7
7 < 4+6
Могут ли быть у треугольника стороны
равные 2,2 и 5?
Почему?
Слайд 54Чему равна сумма углов в треугольнике?
«Оторвите» углы у треугольника и сложите.
Какой
угол вы получили?
Чему равна величина этого угла?
Чему равна сумма «оторванных» углов?
Чему равна величина этого угла?
Чему равна сумма «оторванных» углов?
Сделайте вывод.
Слайд 58Ответь на вопросы:
1 Можно ли быть уверенным, что в каждом треугольнике
сумма
углов равна 180°
углов равна 180°
5 Можно ли измерить углы любого треугольника?
3 Как можно назвать треугольник у которого основание равно
боковой стороне?
4 Периметр равностороннего треугольника равен 6см.
Чему равна сторона треугольника?
2 Существует ли треугольник у которого два прямых угла?
Слайд 61Прямоугольник- это параллелограмм, у
которого все углы прямые.
1. У прямоугольника
противоположные стороны
и углы равны (свойство параллелограмма).
2. Диагонали прямоугольника пересекаются и точкой пересечения делятся пополам (свойство параллелограмма).
3. Диагонали прямоугольника равны.
1. У прямоугольника
противоположные стороны
и углы равны (свойство параллелограмма).
2. Диагонали прямоугольника пересекаются и точкой пересечения делятся пополам (свойство параллелограмма).
3. Диагонали прямоугольника равны.
Слайд 63 Квадрат
-
это прямоугольник, у
которого все стороны равны.
1. Все стороны равны (свойство
ромба).
2. Все углы прямые (свойство
прямоугольника).
3. Диагонали пересекаются и
точкой пересечения делятся
пополам (св-во параллелограмма).
4. Диагонали равны и взаимно
перпендикулярны.
которого все стороны равны.
1. Все стороны равны (свойство
ромба).
2. Все углы прямые (свойство
прямоугольника).
3. Диагонали пересекаются и
точкой пересечения делятся
пополам (св-во параллелограмма).
4. Диагонали равны и взаимно
перпендикулярны.
Слайд 65Параллелограмм
– это четырехугольник,
у которого противоположные
стороны попарно параллельны.
1. У параллелограмма
противоположные стороны и
углы равны.
2. Диагонали параллелограмма
пересекаются и точкой
пересечения делятся пополам.
у которого противоположные
стороны попарно параллельны.
1. У параллелограмма
противоположные стороны и
углы равны.
2. Диагонали параллелограмма
пересекаются и точкой
пересечения делятся пополам.
Слайд 67Ромб
- это параллелограмм, у которого
все
стороны равны.
1. У ромба противоположные стороны и
углы равны (св-во параллелограмма).
2. Диагонали ромба пересекаются и
точкой пересечения делятся
пополам (св-во параллелограмма).
3. Диагонали ромба взаимно
перпендикулярны.
стороны равны.
1. У ромба противоположные стороны и
углы равны (св-во параллелограмма).
2. Диагонали ромба пересекаются и
точкой пересечения делятся
пополам (св-во параллелограмма).
3. Диагонали ромба взаимно
перпендикулярны.
Слайд 69Трапеция
- это
четырехугольник, у
которого две стороны
параллельны, а две
другие нет.
Трапеция называется равнобедренной, если ее боковые стороны равны.
которого две стороны
параллельны, а две
другие нет.
Трапеция называется равнобедренной, если ее боковые стороны равны.
