- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Игры и игровые моменты на уроках математике
Содержание
- 1. Презентация по математике на тему: Игры и игровые моменты на уроках математике
- 2. Игры и игровые моменты на уроках математики.
- 3. «Предмет математики настолько серьезен,что надо не упускать
- 4. «Обучение – это ремесло, использующее бесчисленное количество
- 5. Дидактические игры —
- 6. Главная цель применения математической игры –активизация познавательной деятельности
- 7. При организации дидактических игр с математическим содержанием
- 8. Виды игр на уроках математики :
- 9. Деловая игра «В мире денег»Правила игрыСтартовый
- 10. Тип задач для игры:Задача №1 (стоимость 100
- 11. Деловая игра «Строитель».Задача : произвести настил паркетного
- 12. Побеждает та команда, которая первой выполнить правильный
- 13. Отличителным свойством деловых игр является: моделирование приближенных
- 14. Ролевая игра Тесным образом деловая игра
- 15. По мере сложности ролевые игры делят на
- 16. Игровые формы уроковОсобенно ребята любят, когда весь
- 17. Игровые ситуации Играть на каждом уроке,
- 18. Для создания игровых ситуаций используются исторические экскурсии,
- 19. Считая, что численность войска составляет, например, 100000
- 20. Например, при изучении
- 21. Эта игра очень нравится учащимся.Приятно увидет результат своего труда,да еще опередить остальных товарищей.
- 22. Игра «День рождения»
- 23. Игра «Исправь ошибку» (индивидуальная игра) Учитель
- 24. В виде игры можно проводить и физкультминутки.
- 25. Физкультминутки -благотворно влияют на восстановление умственной работоспособности,- препятствуют
- 26. Очень интересно проходят уроки-сказки и уроки
- 27. Задача. Продавать пшеницу братья едут со скоростью 9,6
- 28. Сказки желательно менять,чтобы детям был интересен урок,чтобы
- 29. Слайд 29
- 30. Слайд 30
- 31. «Играют люди на планете,играют птицы и жуки.Играют
Слайд 3«Предмет математики настолько серьезен,что надо не упускать случая, сделать его занимательным».
Слайд 5 Дидактические игры — это вид учебных занятий,
Дидактическая игра - современный и признанный метод обучения и воспитания, обладающий образовательной, развивающей и воспитывающей функциями, которые действуют в органическом единстве .
Слайд 6
Главная цель применения математической игры –
активизация познавательной деятельности учащихся на уроках математики;
развитие
Слайд 7При организации дидактических игр с математическим содержанием
1.Цель игры. Какие умения и навыки в области математики школьники освоят в процессе игры? Какому моменту игры надо уделить особое внимание? Какие другие воспитательные цели преследуются при проведении игры?
2.Количество играющих. Каждая игра требует определенного минимального или максимального количества играющих. Это надо учитывать при организации игр.
3.Какие дидактические материалы и пособия понадобятся для игры?
4.Как с наименьшей затратой времени познакомить ребят с правилами игры?
5.На какое время должна быть рассчитана игра? Будет ли она занимательной, захватывающей? Пожелают ли ученики вернуться к ней еще раз?
6.Как обеспечить участие всех школьников в игре?
7.Как организовать наблюдение за детьми, чтобы выяснить все ли включились в работу?
8.Какие изменения можно внести в игру, чтобы повысить интерес и активность детей?
9. Какие выводы следует сообщать учащимся в заключение после игры
(лучшие моменты игры, недочеты в игре, результат усвоения
математических знаний, оценки отдельным участникам игры, замечания
по нарушению дисциплины и т.д.)?
Слайд 8Виды игр на уроках математики :
Деловая игра
В деловых играх
Слайд 9 Деловая игра «В мире денег»
Правила игры
Стартовый капитал каждой фирмы –
Командам предлагается по очереди выбирать себе задания, каждое задание имеет определенную стоимость.
Если команда дает правильный ответ, то ее капитал увеличивается на стоимость задания. Если команда дает неправильный ответ, то:
а) капитал уменьшается на 100% стоимости задания, если одна из команд – конкурентов дает правильный ответ;
б) капитал уменьшится на 50%, если и другие команды не смогут дать правильный ответ.
Победителем считается та команда, в чьей фирме будет накоплен больший капитал по окончании игры.
Слайд 10Тип задач для игры:
Задача №1 (стоимость 100 рублей)
Два бизнесмена поспорили: кто
Решение:
1) 5000-3000=2000 рублей
2) (5000-1000)-2000=2000 рублей
Доходы равны
Задача № 2 (стоимость 100 рублей)
В интернет магазине костюм стоит 110 долларов. А в местном супермаркете 5000 рублей. Где дороже, если курс доллара 1:45(один доллар стоит 45 рублей)?
Решение: 110*45=4950 рублей стоит костюм в интернет- магазине.
Дороже в местном супермаркете
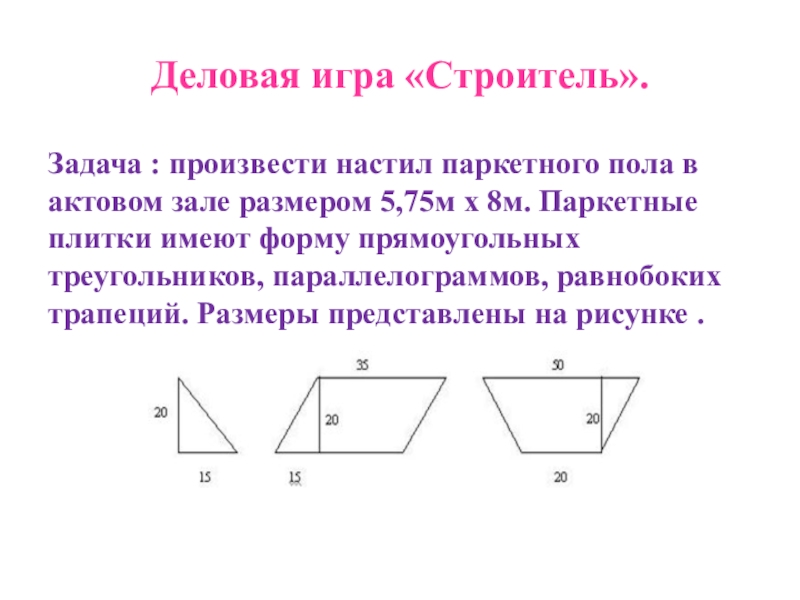
Слайд 11Деловая игра «Строитель».
Задача : произвести настил паркетного пола в актовом зале
Слайд 12
Побеждает та команда, которая первой выполнить правильный расчет. Для этого надо
Подсчеты показывают, что в одном ряду по ширине укладываются по 2 треугольника и по 8 параллелограммов и трапеций.
Действительно, площадь одной полосы шириной 20см и длиной 575 см будет S=20 x 575 = 11500 см2.
Площадь одного треугольника S = 1/2 х 20 х 15 = 150 см2.
Тогда площадь двух треугольников 300 см2.
Площадь параллелограмма S = 20 х 35 = 700см2 .
Площадь трапеции S = (50+20) х 1/2 х 20 = 70 х 10 = 700 см2.
Следовательно, в одной полосе по ширине актового зала поместится по 8 параллелограммов и трапеций:
(11500-300):700=16.
Таких полос в длине зала поместится 800:20=40.
Следовательно, для настила пола понадобится 80 треугольников и по 320 параллелограммов и трапеций.
Слайд 13Отличителным свойством деловых игр является:
моделирование приближенных к реальной жизни ситуаций;
поэтапное развитие
наличие конфликтных ситуаций;
обязательная совместная деятельность участников игры, выполняющих предусмотренные сценарием роли;
использование описания объекта игрового имитационного моделирования;
контроль игрового времени;
элементы состязательности;
правила системы оценок хода и результатов игры.
Слайд 14 Ролевая игра Тесным образом деловая игра связана с ролевой игрой.Ролевая игра
Слайд 15По мере сложности ролевые игры делят на три группы: 1) имитационные
Формы проведения ролевых игр могут быть самыми различными: уроки - суды, воображаемые путешествия, пресс- конференции, дискуссии на основе распределения ролей и т.д. На таких уроках ученики выступают в качестве экспертов, судей, историков, сказочных героев, экскурсоводов, архитекторов и т.д.
Слайд 16
Игровые формы уроков
Особенно ребята любят, когда весь урок проходит в игровой
Примеры игровых форм уроков: урок-сказка, урок-КВН, урок путешествие, урок-кроссворд, урок-смотр знаний, игра «Счастливый случай», «Поле чудес», «Математический биатлон», «Звездный час».
Слайд 17 Игровые ситуации Играть на каждом уроке, наверно, нельзя, чтобы не превратить
Слайд 18Для создания игровых ситуаций используются исторические экскурсии, жизненные факты, занимательные задачи,
Например, у А. С. Пушкина в поэме «Скупой рыцарь» есть такие строки:
«…Читал я где-то,
Что царь однажды воинам своим
Велел снести земли по горсти в кучу,
И гордый холм возвысился,- и царь
Мог с вышины с весельем озирать
И дол, покрытый белыми шатрами,
И море, где бежали корабли».
Слайд 19Считая, что численность войска составляет, например, 100000 человек, объём горсти земли имеет
Слайд 20 Например, при изучении темы «Координатная плоскость» обучающиеся получают интересные
Игра «Соревнование художников»
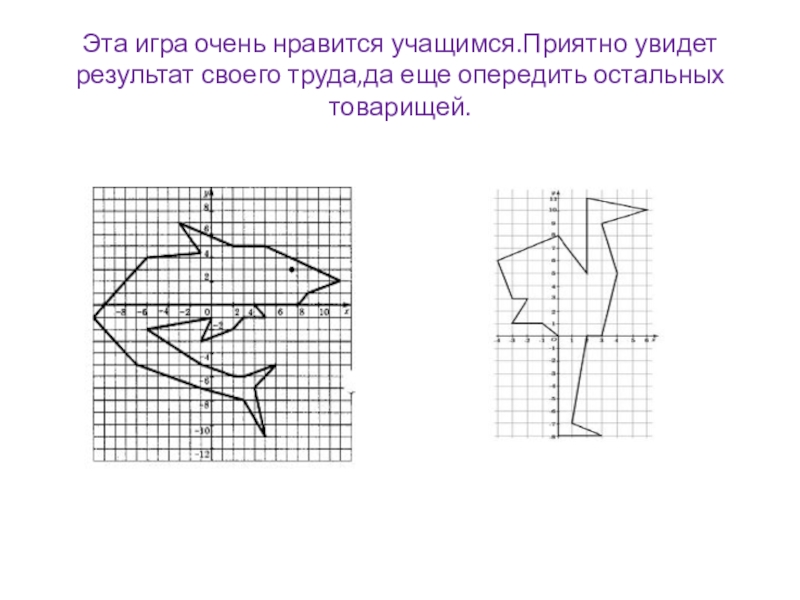
На доске записаны координаты точек: (0;0),(-1;1),(-3;1),(-2;3),(-3;3),(-4;6),(0;8),(2;5),(2;11),(6;10),(3;9),(4;5),(3;0),(2;0),(1;-7),(3;-8),(0;-8),(0;0).
Отметить на координатной плоскости каждую точку и соединить с предыдущей отрезком. Результат – определенный рисунок.
Эту игру можно провести с обратным заданием: нарисовать самим любой рисунок, имеющий конфигурацию ломаной и записать координаты вершин.
Слайд 21Эта игра очень нравится учащимся.Приятно увидет результат своего труда,да еще опередить
Слайд 22
Игра «День рождения»
Очень положительно воспринимается учащимися просьба написать дату своего рождения.
Слайд 23 Игра «Исправь ошибку» (индивидуальная игра) Учитель пишет на доске несколько примеров, часть из
1.
2. (неверно, т.к. )
(неверно, т.к. )
3. 3,7 + 2,251 = 5, 951
4. 5,8 + 3,618 = 8,1418 (неверно, т.к. 5,8 + 3,618 = 9,418)
5. 6,42 . 10 = 6,420 (неверно, т.к. 6,42 ? 10 = 64,2)
6. 0,006 . 100 = 0,6
7. 4,4 тыс. = 44000 (неверно, т.к. 4,4 тыс. = 4,4 . 1000 = 4400)
8. 0,054 . 100 = 0,54 (неверно, т.к. 0,054 . 100 = 5,4)
9. 8,3 – 4,7 = 44 (неверно, т.к. 8,3 – 4,7 = 3,6)
10. 6,8 – 5,1 = 1,7
11. 45,531 : 10 = 4,531
12. 0,046 : 10 = 0,46 (неверно, т.к. 0,046 : 10 = 0,0046)
Слайд 25Физкультминутки
-благотворно влияют на восстановление умственной работоспособности,
- препятствуют нарастанию утомления,
- повышают эмоциональный уровень
- снимают статические нагрузки.
- способствуют укреплению здоровья
Слайд 26 Очень интересно проходят уроки-сказки и уроки –путешествия.Например сказка «Конек –
Сказки и путешествия лучше проходят во время повторения и обобщения
Слайд 27Задача. Продавать пшеницу братья едут со скоростью 9,6 км/ч и тратят на
Слайд 28Сказки желательно менять,чтобы детям был интересен урок,чтобы интерес к предмету не
На сайте инфоурок я размещаю свои материалы.
ИнфоурокИнфоурок›Математика›Презентации›Урок-путешествие по математике "Сложение и вычитание отрицательных чисел и чисел с разными знаками"
ИнфоурокИнфоурок›Математика›Презентации›Урок-сказка по математике "Конек-горбунок" (презентация)
Инфоурок Инфоурок›Математика›Конспекты›Сценарий математического конкурса между 6 – ми классами "Удивительные приключения Буратино".
ИнфоурокИнфоурок›Математика›Презентации›Математический конкурс "Выбор наследника престола"(презентация)
ИнфоурокИнфоурок›Математика›Презентации›Математическая сказка "Необычайные приключения Ивана-Царевича". (Презентация внеклассного мероприятия))
И другие
Слайд 31
«Играют люди на планете,играют птицы и жуки.
Играют все, но только дети
И если в школе на уроке вдруг поведется поиграть,
То нет счастливей их на свете и выучат все всё на
пять.»
К.Г.Ушинский