физики
Костенкова С.С.
2016
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Формула Ньютона Лейбница
Содержание
- 1. Презентация по математике на тему: Формула Ньютона Лейбница
- 2. Интеграл и его применение.Первым известным методом для
- 3. Этот метод был подхвачен и развит Архимедом,
- 4. В конце XVII века была открыта связь
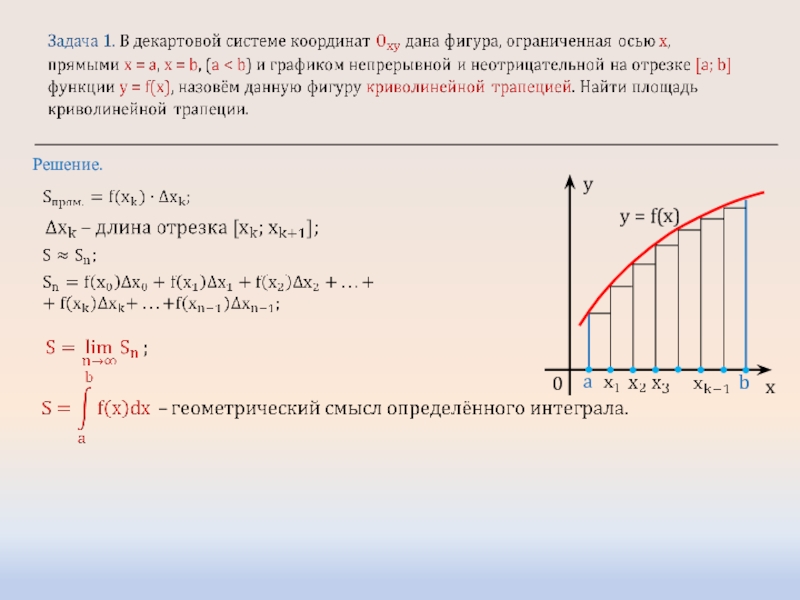
- 5. Применение интеграла для вычисления площади криволинейной трапеции
- 6. Криволинейная трапеция Криволинейной трапецией называется фигура,
- 7. Решение. yx0a by = f(x)
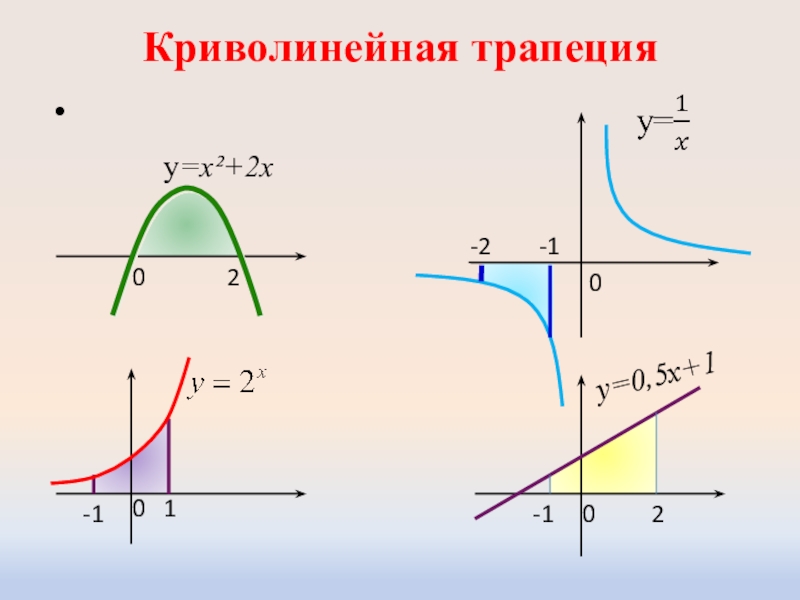
- 8. Криволинейная трапеция 020001-1-12-1-2y=х²+2хy=0,5х+1
- 9. Какие из заштрихованных на рисунке фигур являются
- 10. Задача Изобразить криволинейную трапецию, ограниченную графиком функции
- 11. Площадь криволинейной трапеции. Площадь криволинейной
- 12. Алгоритм нахождения площади криволинейной трапеции: Изобразить
- 13. Задача: Вычислить площадь фигуры, ограниченной линиями Решение113y=х²Ответ:
- 14. Вычислите площадь фигуры, ограниченной линиями 1.2.3.Домашнее задание4.5. Домашнее задание
- 15. Выражение площади криволинейной трапеции через определенный интеграл
- 16. Геометрический смысл определенного интеграла1.
- 17. Геометрический смысл определенного интеграла2.
- 18. Геометрический смысл определенного интеграла
- 19. Интегральная формула теоремы Ньютона – Лейбница
- 20. Нахождение площади плоской фигуры 1. Найти площадь
- 21. Пример№2 Найти площадь одной арки синусоиды.
- 22. Вычислите (предварительно сделав рисунок) площадь фигуры,
- 23. Домашнее заданиеУчебник М.И. Башмаков (11 класс)Стр.176 1)
- 24. Применение интеграла для вычисления площадей плоских фигур Гиперссылкаhttps://www.youtube.com/watch?v=7sOCm9T4_98https://www.youtube.com/watch?v=n3Sv-D2ylyU
Интеграл и его применение.Первым известным методом для расчета интегралов является метод исчерпывания Евдокса (примерно 370 до н.э.), который пытался найти площади и объемы фигур, разрывая их на бесконечное множество частей, для которых площадь или объем уже
Слайд 1Площади плоских фигур.
Формула Ньютона-Лейбница. Площадь криволинейной трапеции.
ГБПОУ КДПИ им. К Фаберже
Преподаватель
Слайд 2Интеграл и его применение.
Первым известным методом для расчета интегралов является метод
исчерпывания Евдокса (примерно 370 до н.э.), который пытался найти площади и объемы фигур, разрывая их на бесконечное множество частей, для которых площадь или объем уже известны.
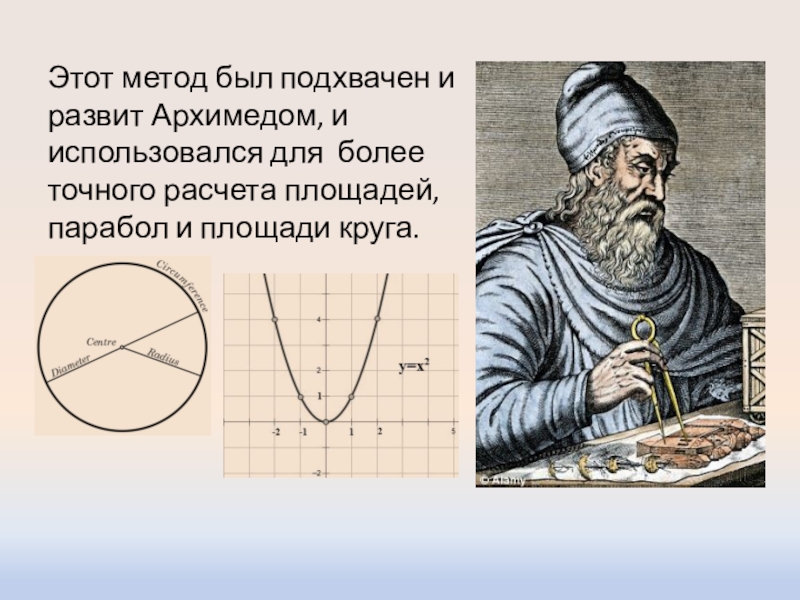
Слайд 3Этот метод был подхвачен и развит Архимедом, и использовался для более
точного расчета площадей, парабол и площади круга.
Слайд 4В конце XVII века была открыта связь между вопросами измерения и
теорией функции.
Эта связь в ее простейшем виде сформулирована в виде теоремы, которой дали имена основоположников математического анализа – Ньютона и Лейбница.
Эта связь в ее простейшем виде сформулирована в виде теоремы, которой дали имена основоположников математического анализа – Ньютона и Лейбница.
Слайд 6
Криволинейная трапеция
Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].
Отрезок [a;b] называют основанием
этой криволинейной трапеции
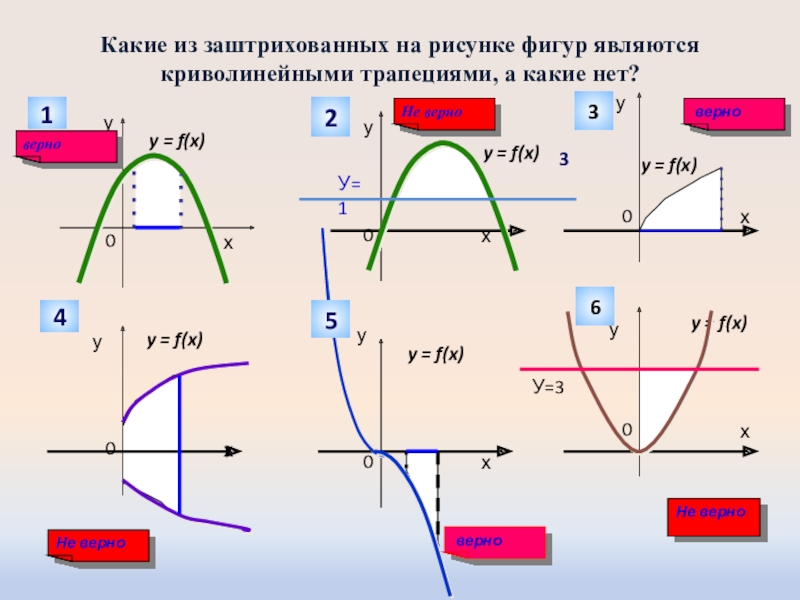
Слайд 9Какие из заштрихованных на рисунке фигур являются криволинейными трапециями, а какие
нет?
у
1
у
у
у
у
у
У=1
2
3
3
y = f(x)
y = f(x)
y = f(x)
y = f(x)
y = f(x)
y = f(x)
У=3
4
5
6
верно
Не верно
верно
Не верно
верно
Не верно
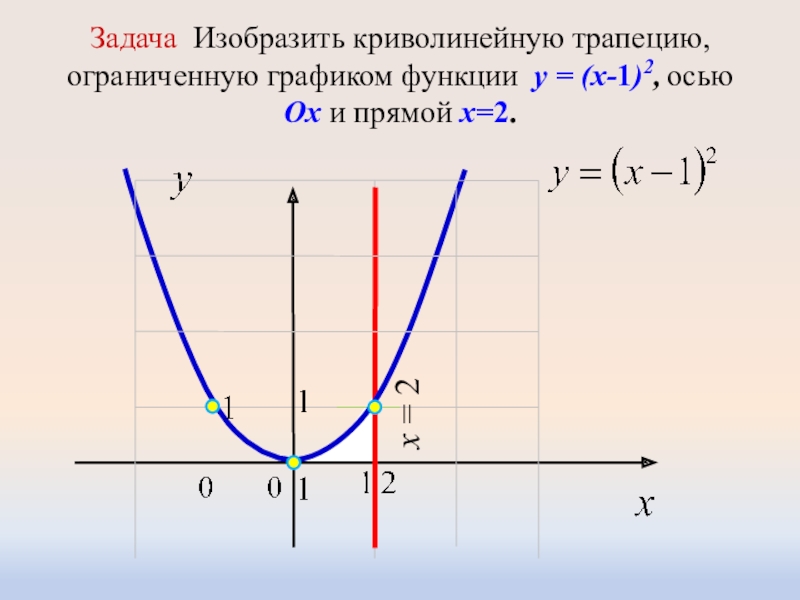
Слайд 10Задача Изобразить криволинейную трапецию, ограниченную графиком функции y = (x-1)2, осью
Ox и прямой x=2.
x = 2
Слайд 11
Площадь криволинейной трапеции.
Площадь криволинейной трапеции вычисляется по формуле:
S = F(b) - F(a)
Разность F(b) - F(a) называю интегралом от функции f(x) на отрезке [a, b] и обозначают так :
Слайд 12
Алгоритм нахождения площади криволинейной трапеции:
Изобразить чертеж и убедится, является ли данная
фигура криволинейной трапецией
Найти первообразную: F(x)
Найти первообразную: F(b) и F(a)
Применить формулу, вычислив разность:
S=F(b)-F(a)
Найти первообразную: F(x)
Найти первообразную: F(b) и F(a)
Применить формулу, вычислив разность:
S=F(b)-F(a)
Слайд 20Нахождение площади плоской фигуры
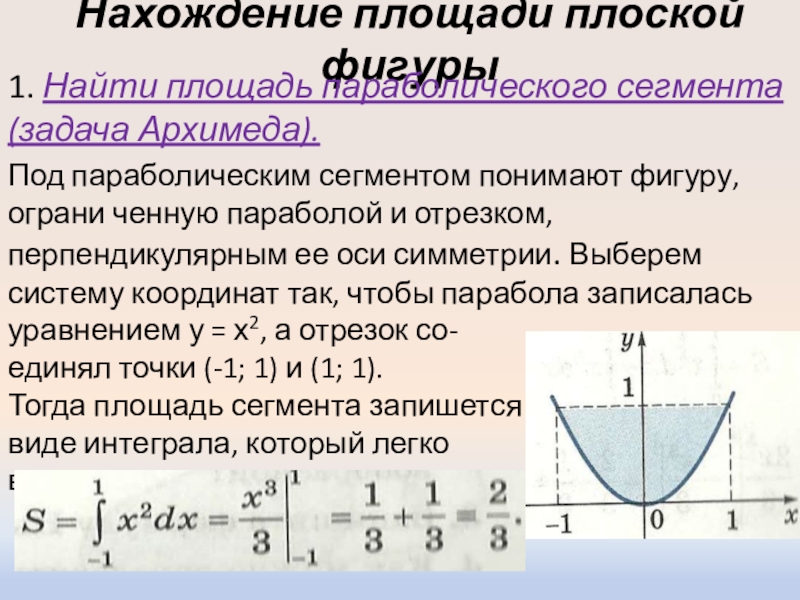
1. Найти площадь параболического сегмента (задача Архимеда).
Под
параболическим сегментом понимают фигуру, ограни ченную параболой и отрезком, перпендикулярным ее оси симметрии. Выберем систему координат так, чтобы парабола записалась уравнением у = х2, а отрезок со-
единял точки (-1; 1) и (1; 1).
Тогда площадь сегмента запишется в
виде интеграла, который легко
вычисляется:
Тогда площадь сегмента запишется в
виде интеграла, который легко
вычисляется:
Слайд 21Пример№2
Найти площадь одной арки синусоиды.
Искомая площадь:
Пример№3
Найти площадь фигуры, заключенной между дугами парабол у = х2 и у = √х.
Данная фигура ограничена графиками
двух функций:
Тогда:
Пример№3
Найти площадь фигуры, заключенной между дугами парабол у = х2 и у = √х.
Данная фигура ограничена графиками
двух функций:
Тогда:
Слайд 23Домашнее задание
Учебник М.И. Башмаков (11 класс)
Стр.176
1) №27,
2) задание из
презентации.
Ответить на вопросы:
1. Что такое криволинейная трапеция?
2. Как вычисляется площадь криволинейной трапеции с помощью понятия первообразной?
3. Запишите формулу Ньютона—Лейбница.
4. Как можно определить интеграл через первообразную?
Ответить на вопросы:
1. Что такое криволинейная трапеция?
2. Как вычисляется площадь криволинейной трапеции с помощью понятия первообразной?
3. Запишите формулу Ньютона—Лейбница.
4. Как можно определить интеграл через первообразную?




![Презентация по математике на тему: Формула Ньютона Лейбница Криволинейная трапеция Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и Криволинейная трапеция Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака](/img/thumbs/cd2ee1a706b6e0ee10b197a822b33e2e-800x.jpg)