- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Элементы комбинаторики, статистики и теории вероятности.
Содержание
- 1. Презентация по математике на тему Элементы комбинаторики, статистики и теории вероятности.
- 2. Множества и операции над ними
- 3. Определение 1Если каждый элемент множества В является
- 4. Определение 2:Пересечением множеств А и В называют
- 5. Определение 3:Объединением множества А и В называют
- 6. Комбинаторные задачи
- 7. Определение:Комбинаторика – раздел математики, в котором изучаются
- 8. Где в реальной жизни решают комбинаторные задачи?Конструкторы
- 9. Комбинаторика становится наукой лишь в XVIII веке,
- 10. Пример: Из цифр 1,5,9 следует составить трехзначное
- 11. Пример:Перечислить все возможные цветовые сочетания брюк и
- 12. Правило умножения:Для того чтобы найти число всех
- 13. Пример: Несколько стран мира в качестве символа
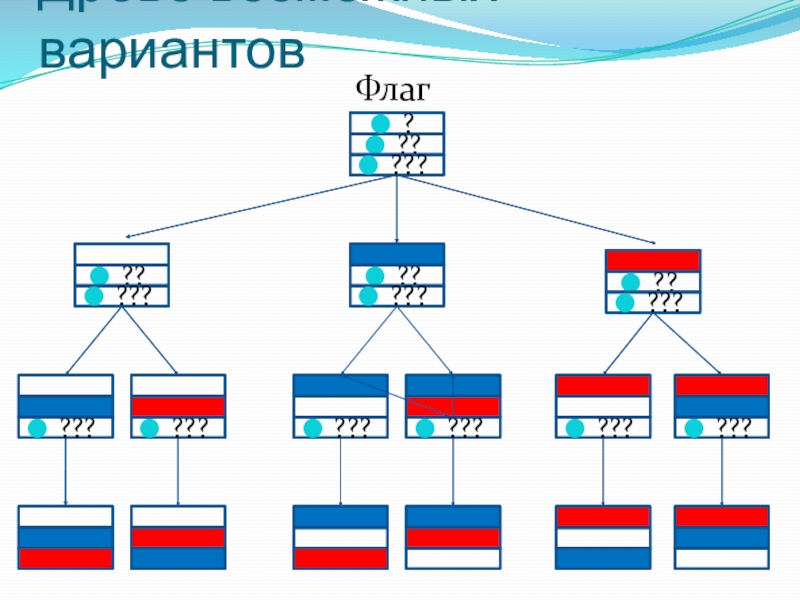
- 14. Древо возможных вариантовФлаг
- 15. Пример: В семье – 6 человек, и
- 16. Определение: Произведение первых подряд идущих n натуральных чисел обозначают Pn=n!
Множества и операции над ними
Слайд 3Определение 1
Если каждый элемент множества В является элементом множества А, то
множество В называют подмножеством множества А.
Обозначение: .
Знак называют знаком включения.
Обозначение: .
Знак называют знаком включения.
Слайд 4Определение 2:
Пересечением множеств А и В называют множество, состоящее из всех
общих элементов множеств А и В, т.е. из всех элементов, которые принадлежат множеству А, и множеству В.
Обозначение:
Обозначение:
Слайд 5Определение 3:
Объединением множества А и В называют множество, состоящее из всех
элементов, которые принадлежат хотя бы одному из этих множеств – или множеству А, или множеству В.
Обозначение:
Обозначение:
Слайд 7Определение:
Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько
различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Слайд 8Где в реальной жизни решают комбинаторные задачи?
Конструкторы при создании новой модели
механизма;
Агрономы при планировании размещения культур;
Химики при изучении строения органических молекул.
История возникновения комбинаторики:
Древний Китай
Древняя Греция (подсчет числа различных комбинаций длинных и коротких шагов в стихотворных размерах);
Игра и комбинаторика (шашки, шахматы, домино, кости, карты).
Агрономы при планировании размещения культур;
Химики при изучении строения органических молекул.
История возникновения комбинаторики:
Древний Китай
Древняя Греция (подсчет числа различных комбинаций длинных и коротких шагов в стихотворных размерах);
Игра и комбинаторика (шашки, шахматы, домино, кости, карты).
Слайд 9Комбинаторика становится наукой лишь в XVIII веке, когда возникла теория вероятностей.
Выяснилось,
что центральное место в элементарной комбинаторике занимают задачи, для решения которых либо надо перебрать все возможные варианты комбинаций, либо определить число таких вариантов, либо сделать и то и другое.
Слайд 10Пример:
Из цифр 1,5,9 следует составить трехзначное число без повторяющихся цифр.
Решение: 159,
195,
519, 591,
915, 951.
Значит, всего можно составить 6 таких чисел.
Мы привели не случайный, а организованный подбор.
519, 591,
915, 951.
Значит, всего можно составить 6 таких чисел.
Мы привели не случайный, а организованный подбор.
Слайд 11Пример:
Перечислить все возможные цветовые сочетания брюк и свитера, если в гардеробе
имеются брюки трех цветов серые, бежевые и черные, и свитера трех цветов – зеленый, песочный и белый.
Составим таблицу:
Ответ : 9 вариантов
Составим таблицу:
Ответ : 9 вариантов
Слайд 12Правило умножения:
Для того чтобы найти число всех возможных исходов независимого проведения
двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Пример
Слайд 13Пример:
Несколько стран мира в качестве символа своего государства решили использовать
флаг в виде трех горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику при условии, что у каждой страны, свой, отличный от других, флаг?
Слайд 15Пример:
В семье – 6 человек, и за столом в кухне
стоят 6 стульев. Семья решила каждый вечер, ужиная, рассаживаться на эти 6 стульев по-новому. Сколько дней члены семьи смогут осуществлять задуманное?
6*5*4*3*2*1=720